Деформация изгиба

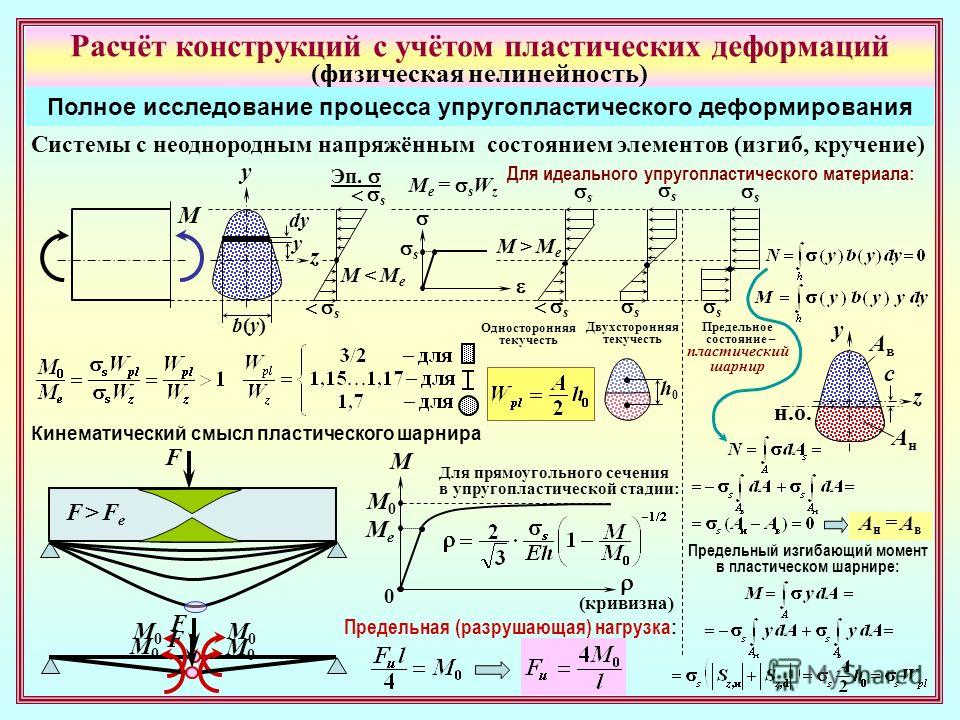
Пластическая и упругая деформация

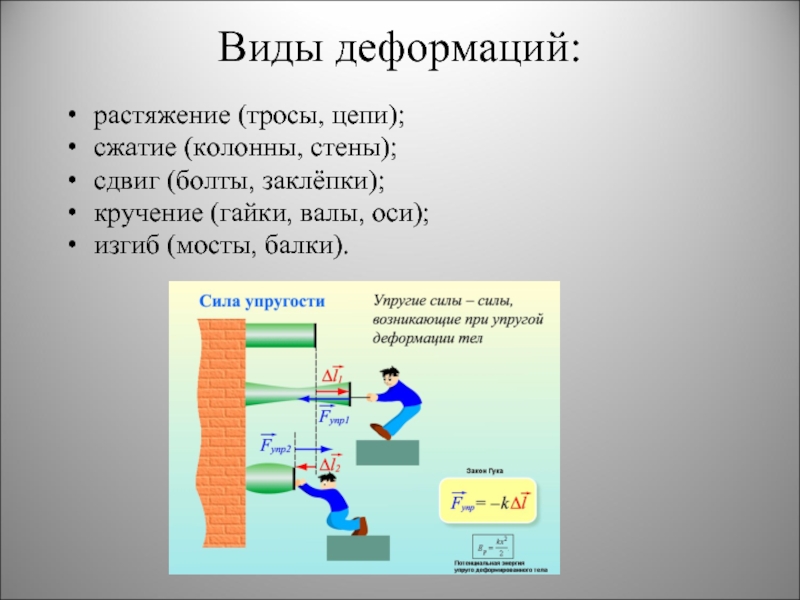
В процессе деформации важное значение имеет величина межатомных связей, приложение нагрузки достаточной для их разыва приводит к необратимым последствиям (необратимая или пластическая деформация). Если нагрузка не превысила допустимых значений, то тело может вернуться в исходное состояние (упругая деформация). Простейший пример поведения предметов, подверженных пластической и упругой деформацией, можно проследить на падении с высоты резинового мяча и куска пластилина

Резиновый мяч обладает упругостью, поэтому при падении он сожмется, а после превращения энергии движения в тепловую и потенциальную, снова примет первоначальную форму. Пластилин обладает большой пластичностью, поэтому при ударе о поверхность оно необратимо утратит свою первоначальную форму

Простейший пример поведения предметов, подверженных пластической и упругой деформацией, можно проследить на падении с высоты резинового мяча и куска пластилина. Резиновый мяч обладает упругостью, поэтому при падении он сожмется, а после превращения энергии движения в тепловую и потенциальную, снова примет первоначальную форму. Пластилин обладает большой пластичностью, поэтому при ударе о поверхность оно необратимо утратит свою первоначальную форму.

За счет наличия деформационных способностей все известные материалы обладают набором полезных свойств – пластичностью, хрупкостью, упругостью, прочностью и другими. Исследование этих свойств достаточно важная задача, позволяющая выбрать или изготовить необходимый материал. Кроме того, само по себе наличие деформации и его детектирование часто бывает необходимо для задач приборостроения, для этого применяются специальные датчики называемые экстензометрами или по другому тензометрами.

Главные понятия

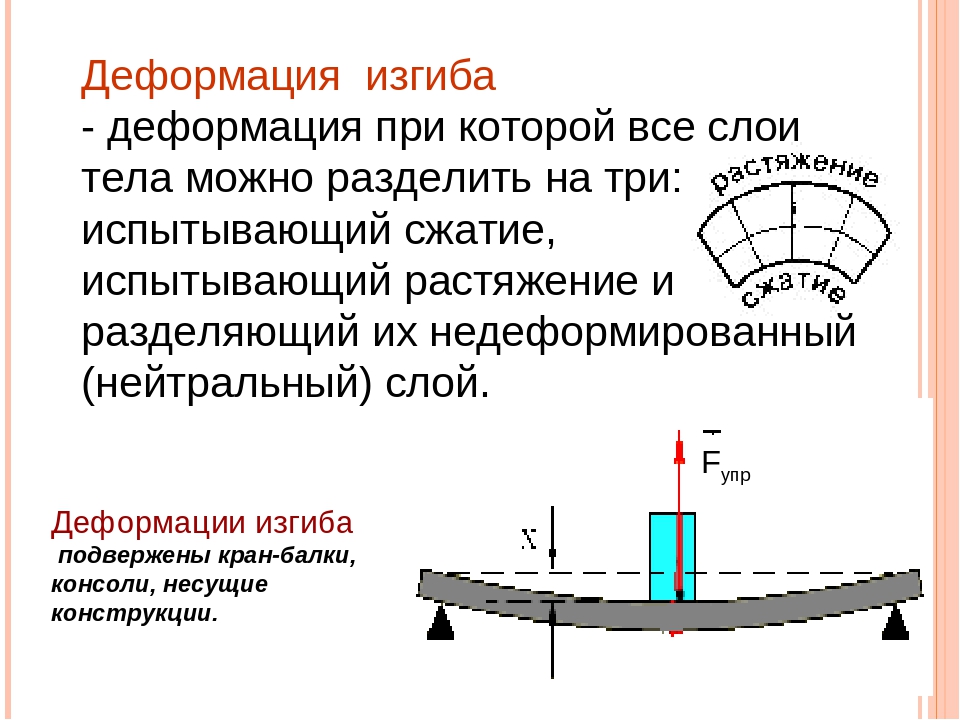
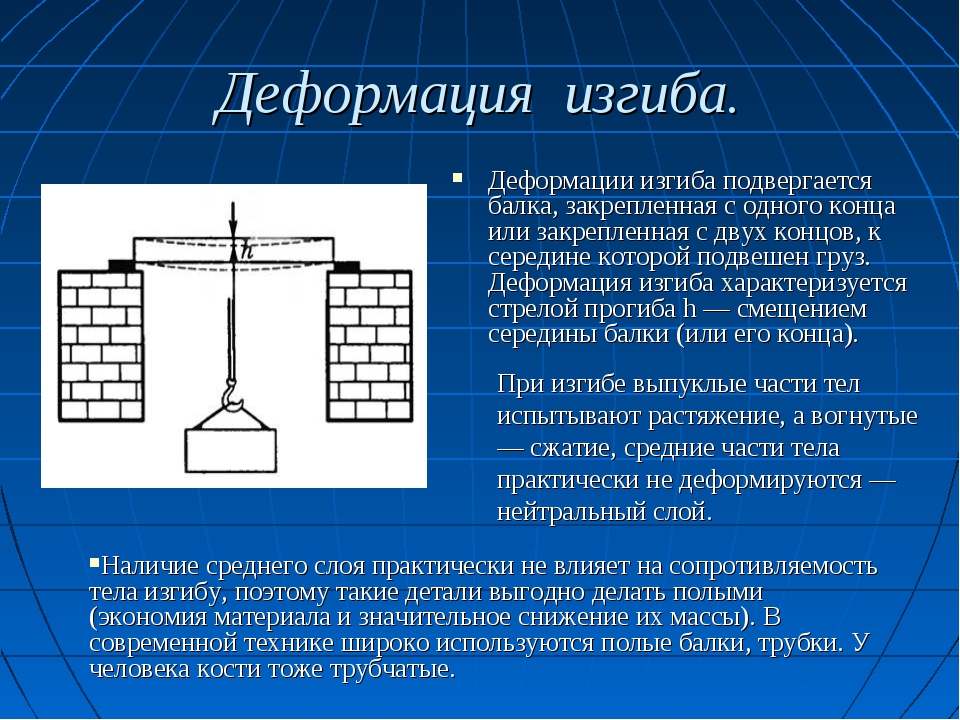
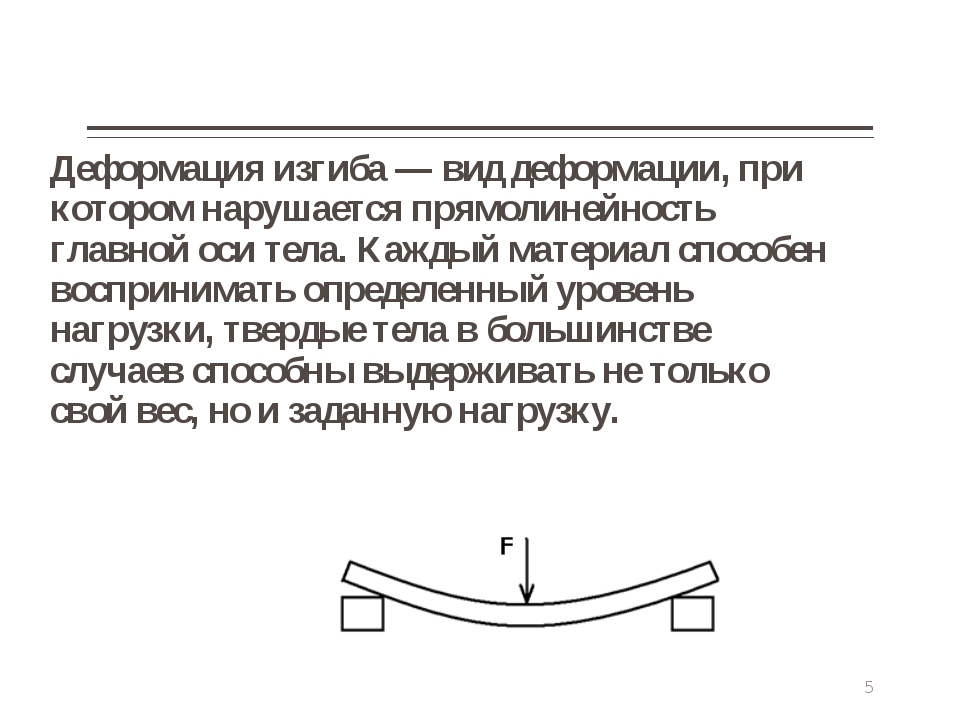
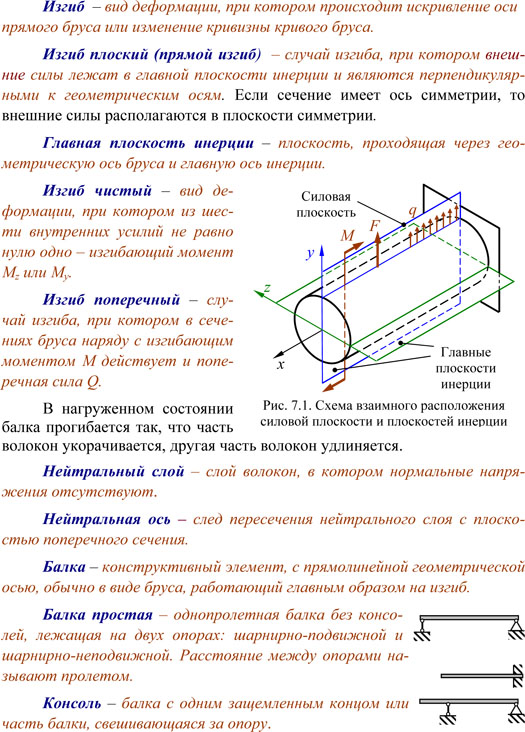
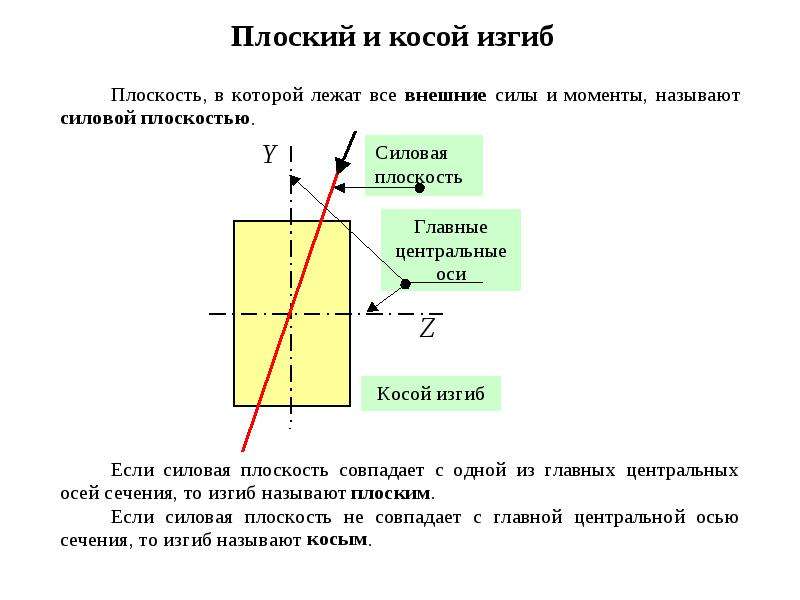
Под изгибом детали знают природное или искусственное изменение формы. Данный процесс делится на две категории – плоский или косой. В первом варианте ось детали хранит своё первое положение, в другом происходит её изменение в горизонтальной или плоскости расположенной вертикально.

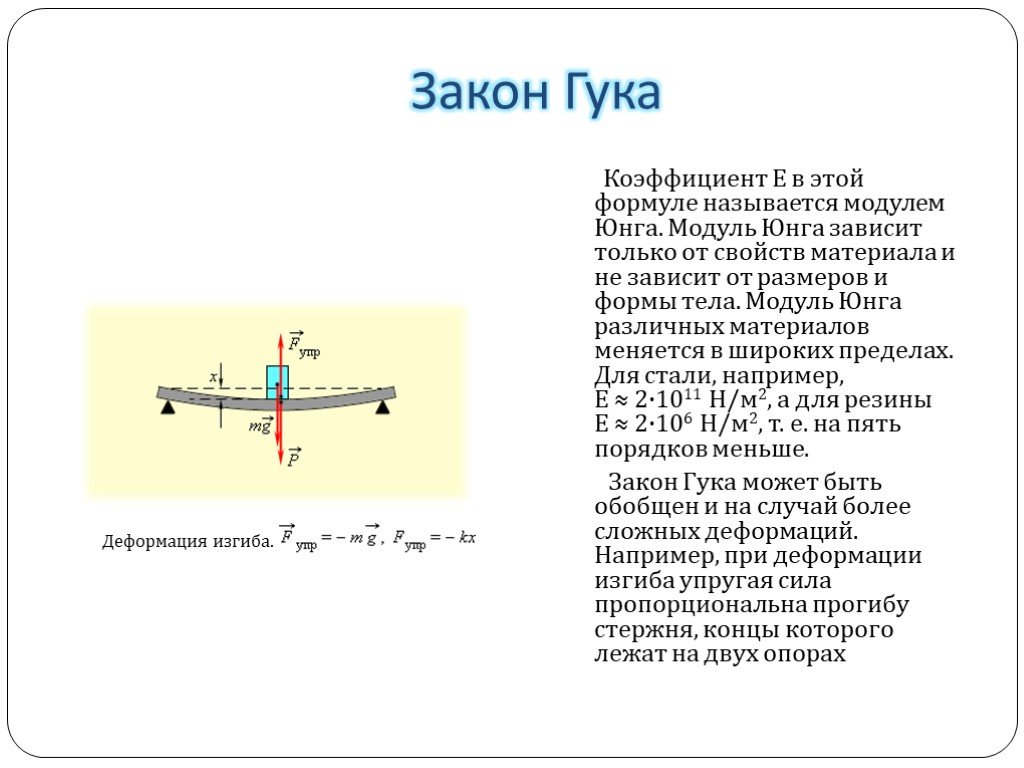
Ключевым теоретическим положением, определяющим физические процессы, протекающие в результате изгиба, считается закон Гука. Опираясь на него величина деформации (изгиба), пропорциональна приложенной к этому телу силе. Для любого из видов деформации разработан персональный расчёт действующих параметров.

Оценка степени воздействия действующих факторов на деформацию выполняется при помощи следующих критериев:

• поверхностной площади подверженной деформации;
• длины детали;
• силы, воздействующие на конструкцию;
• модуль упругости (его безоговорочный критерий);
• величина и характер изменения модуля длины в результате упругой деформации.

Одним из основных параметров считается вероятная энергия деформации при изгибе. На основании таких параметров делают обозначение модуля Юнга. Воспользовавшись его помощью рассчитывают скорость распространения продольной волны. Величина механического напряжения, при которой дефармация тела все ещё будет упругой, а сам объект способен реконструировать начальную форму после снятия нагрузки, именуется пределом упругости. При превышении возможного значения данного параметра тело начнёт разрушаться. Этот предел именуется прочностью. При оценке показателей прочности используют следующие предположения:

1. О постоянстве нормальных стрессов. Она определяет постоянство расстояний при появлении стрессов изгиба.
2. Плоскости сечений. Оно именуется гипотезой Бернулли. Сечения детали в спокойном положении будут в плоском состоянии. После деформации они берегут начальную форму, но разворачиваются относительно некоторой линии. Она именуется нейтральной осью.
3. Отсутствие давлений на боковые поверхности. Считается, что соседние волокна не давят один на один.

Перечисленные гипотезы дают возможность оценить деформации сдвига и характер изгиба каждого слоя исследуемой детали. Это происходит в результате влияния самых разных сил. Нагрузки вызывают деформацию изгиба в самых разнообразных плоскостях. Они делятся на две категории:

• характеру влияния (статические или динамические);
• степени влияния (массовые или объёмные);
• поверхности (сосредоточенные, влияют на некоторые детали поверхности и распределёнными – на каждый сантиметр поверхности).

К статическим относятся нагрузки, у которых место приложения и направления сил не меняется или изменяются неторопливо в течение определённого временного промежутка. К подобным нагрузкам относится сила тяжести. В данном случае можно принять заявление, что детали физического объекта находятся в состоянии равновесия. У динамических нагрузок данные параметры меняются очень быстро или носят импульсивный характер. К ним можно отнести ударные нагрузки при забивке свай, отделке металла ковкой, влияние неровностей дороги на колесо.

При сосредоточенной статической нагрузке на отдельный участок поверхности бруса происходит его дефармация в сторону в направлении сил взаимные действия. Для расчёта показателей характеризующих главные показатели состояния деформированного тела используют дифференциальные уравнения, которые дают возможность обнаружить существующие практичные связи. По деформации изгиба при помощи модуля Юнга можно определить крепость исследуемого элемента конструкции (балки, бруса, подвесной опоры и т. д.). На основании полученных областей решения можно выстроить графическое изображение силы упругости, которое воочию показывает, что происходит с самыми разными участками деформированной детали. Для каждой детали в зависимости от её геометрических размеров, материала изготовления и величины приложенных сил выведена собственная формула.

Для наглядности понимания характера протекающих процессов применяет метод нанесения эпюр на поверхность объекта. Данная операция именуется топология. Главной идеей считается проецирование линий нагрузки на соответствующую поверхность (горизонтальную, фронтальную или профильную). В современных методах топологии используют фрактальную геометрию.

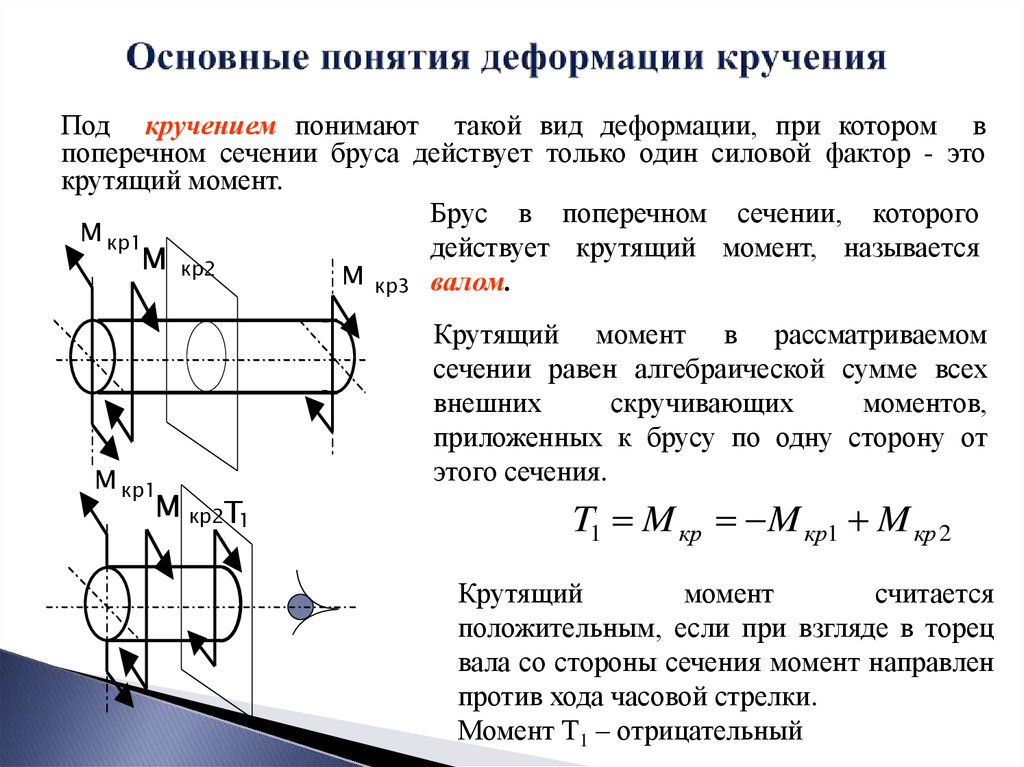
Кручение

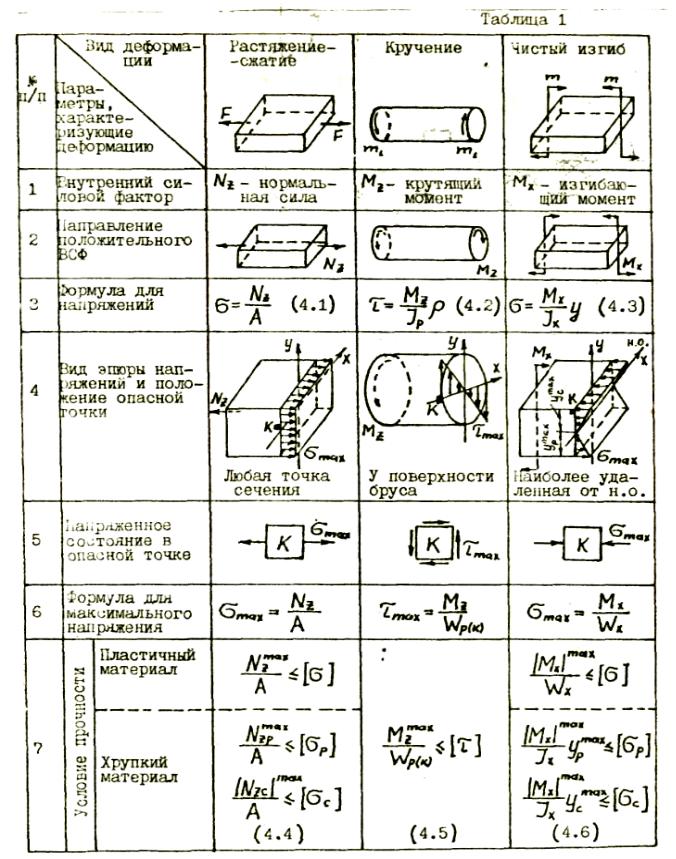
Кручение — один из видов деформации тела. Возникает в том случае, если нагрузка прикладывается к телу в виде пары сил (момента) в его поперечной плоскости. При этом в поперечных сечениях тела возникает только один внутренний силовой фактор — крутящий момент. На кручение работают пружины растяжения-сжатия и валы. При деформации кручения смещение каждой точки тела перпендикулярно к её расстоянию от оси приложенных сил и пропорционально этому расстоянию.

Деформацию кручения можно наблюдать, если на стержень, один конец которого закреплен, действует пара сил, лежащих в плоскости, перпендикулярной оси стержня. При кручении отдельные слои тела остаются параллельными, но поворачиваются друг относительно друга на некоторый угол. Деформация кручения представляет собой неравномерный сдвиг. Деформации кручения возникают при завинчивании гаек, при работе валов машин.

Пример деформации кручения цилиндрического стержня

Если проволоку или стержень, закрепленные с одного конца, закручивать, прилагая к другому концу пару сил F с моментом, равным М, то стержень (проволока) претерпевает деформацию кручения, при которой одно его основание поворачивается по отношению к другому, фиксированному, на некоторый угол φ – угол кручения (рис. 1; 2).

Рис. 1.

Отношение угла закручивания φ к длине называют относительным углом закручивания

Закон Гука для малых деформаций кручения выражается формулой

M = Gкр.j

где Gкр.– модуль кручения.

Модуль кручения , помимо материала, зависит также от формы и размеров тела.

Представьте, перед вами цилиндр (или проволока). Если вы начнёте его (её) верхний конец поворачивать вдоль оси, закрепив нижний конец, то при повороте верхней грани на один радиан вы прикладываете вращающий момент, в точности равный модулю кручения (рис.1; 2). Это и есть его определение.

Модуль кручения Gкр показывает, какой момент силы нужно приложить, чтобы закрутить проволоку на угол в 1 рад.

Рис. 2.

Деформация кручения является частным случаем деформации сдвига.

Сдвиг

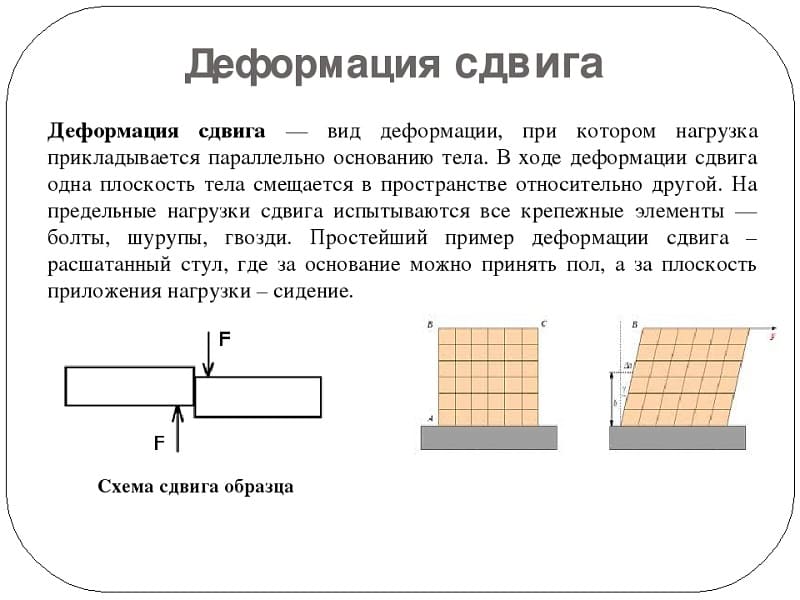
Сдвигом называют такую деформацию твердого тела, при которой все его плоские слои, параллельные некоторой плоскости сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу (рис. 3).

Рис. 3.

Деформация сдвига возникает под действием сил, приложенных к двум противоположным граням тела так, как показано на рисунках 3; 4. Эти силы вызывают смещение слоев тела, параллельных направлению сил. Расстояние между слоями не изменяется. Любой прямоугольный параллелепипед, мысленно выделенный в теле, превращается в наклонный.

Рис. 4.

Мерой деформации сдвига является угол сдвига γ — угол наклона вертикальных граней (рис. 5).

Рис. 5.

Сдвиг происходит под действием касательной силы F, приложенной к грани ВС, параллельной плоскости сдвига. Грань АД, параллельная ВС, закреплена неподвижно.

Так как угол мал, формулу можно записать в виде:

где СС1 = D X — абсолютный сдвиг, γ — угол сдвига, называемый также относительным сдвигом, выражается в радианах.

По закону Гука относительный сдвиг γ пропорционален касательному напряжению τ = F/S, где S — площадь поверхности грани ВС, т.е.

τ = F / S = Gg

где G — модуль сдвига.

Закон Гука для малой деформации сдвига выражается формулой:

Коэффициент G, зависящий от материала тела, называется модулем сдвига и характеризует упругие свойства тела при деформации сдвига. Например, для стального образца G = 76 ГПа.

Модуль сдвига равен касательному напряжению, которое возникло бы в образце при относительном сдвиге, равном 1 (при условии, что закон Гука выполняется).

Деформацию сдвига испытывают, например, заклепки и болты, соединяющие металлические конструкции. Сдвиг при больших углах приводит к разрушению тела — срезу. Срез происходит при работе ножниц, пилы и др.

Обратите внимание на принципиальное отличие модуля кручения от модуля сдвига, который зависит только от материала. Модуль кручения зависит не только от материала, но ещё и от диаметра и от длины цилиндра

Расчёты на прочность при сдвиге

Оценка прочностных характеристик изделий производится для определения наступления трёх моментов деформации:

1. Смещение отдельных слоёв (появления угла деформации).
2. Смятие элементов крепления.
3. Сдвиг.
4. Разрыв.

Расчёт на прочность необходим для определения условий наступления каждого из видов. На практике для более наглядной оценки характеристик прочности и стойкости к деформации решают существующие аналитические выражения и изображают эпюры отражающие направления воздействия различных видов напряжений.

Получение численных характеристик возможно благодаря применению разработанных методов решения систем дифференциальных уравнений. Уточнение аналитических выражений производится на основе принятых гипотез.

Расчёт допустимых напряжений производится на основании первой, третьей и четвёртой гипотезы прочности. Каждая из гипотез принимается для различных материалов, обладающих своими физико-механическими характеристиками.

Прочность находиться на каждом из этапов разработки конкретной детали. Сначала вычисляют величины допустимых напряжений и угол отклонения на предварительном (проверочном) этапе. Это позволяет определить их уровни, величины и направление приложенных сил. После этого приступают к проектированию. На этом этапе производится выбор материала детали и крепёжных элементов с учётом необходимой прочности каждого элемента конструкции. На конечном этапе ещё раз проверяют допустимые нормы нагрузки и способность готовой детали выдерживать допустимую и дополнительную нагрузку, то есть определяют запас прочности.

Наиболее показательными являются расчёты для чистого сдвига. В этом случае при расчёте рассматривают следующие аспекты решения задачи:

• Статический (составляется уравнение равновесия). В этом случае используется предположение о равномерности распределения касательных напряжений. Однако в некоторых случаях они распределяются не равномерно, что усложняет решение поставленной задачи. Он позволяет установить связь возникших напряжений с действующими внешними силами. Это производиться благодаря получению семейства решений дифференциальных уравнений равновесия для всего объёма детали.
• Геометрический (деформационный). Позволяет отобразить связь между отдельными небольшими участками исследуемой детали.
• Математический. Позволяет выбрать метод решения составленной системы уравнений. Провести математическое моделирование протекающих процессов.
• Физический. Устанавливает связь между физическими процессами при деформации с учётом физических свойств материала и возникшими напряжениями (механическими свойствами).

На математическом и физическом этапе рассмотрения поставленной задачи применяются следующие основные расчетные выражения и допущения:

• закон Гука для деформации смещения;
• гипотезы прочности (с учётом физических и механических свойств выбранного материала);
• выбор системы эквивалентных напряжений;
• упрощения при изображении эпюр, отображающих направления действующих сил и возникших напряжений;
• принятие основных положений для случая чистого сдвига.

В первом случае происходит пластическая деформация детали, когда интенсивность возникших напряжений превышает предел текучести выбранного материала. Размеры такой деформации зависят от характера и интенсивности действия внешних сил, показателей прочности материала, изменения температурного режима.

При интенсивности воздействия, превышающем прочность материала, происходит разрыв. Оба эти процесса приводят к нарушению механических соединений деталей (например, метизов, заклёпок, втулок).

Разработанные методы расчёта прочности позволяют проектировать и изготавливать детали с заданием, превышающим этот предел. Это позволяет существенно повысить надёжность и долговечность всей конструкции. В настоящее время разработан стройный математический аппарат создания моделей допустимой деформации. Его реализуют с применением созданных программных средств, которые позволяют получить числовые характеристики прочности и построить графические изображения эпюр в формате 3D графики.

Метод Мора.

Порядок определения перемещений по методу Мора:

1. Строится «вспомогательная система» и нагружается единичной нагрузкой в точке, где требуется определить перемещение. Если определяется линейное перемещение, то в его направлении прикладывается единичная сила, при определении угловых перемещений – единичный момент.

2. Для каждого участка системы записываются выражения изгибающих моментов М_f от приложенной нагрузки и М₁ – от единичной нагрузки.

3. По всем участкам системы вычисляют и суммируют интегралы Мора, получая в результате искомое перемещение:

4. Если вычисленное перемещение имеет положительный знак, то это значит, что его направление совпадает с направлением единичной силы. Отрицательный знак указывает на то, что действительное перемещение противоположно направлению единичной силы.

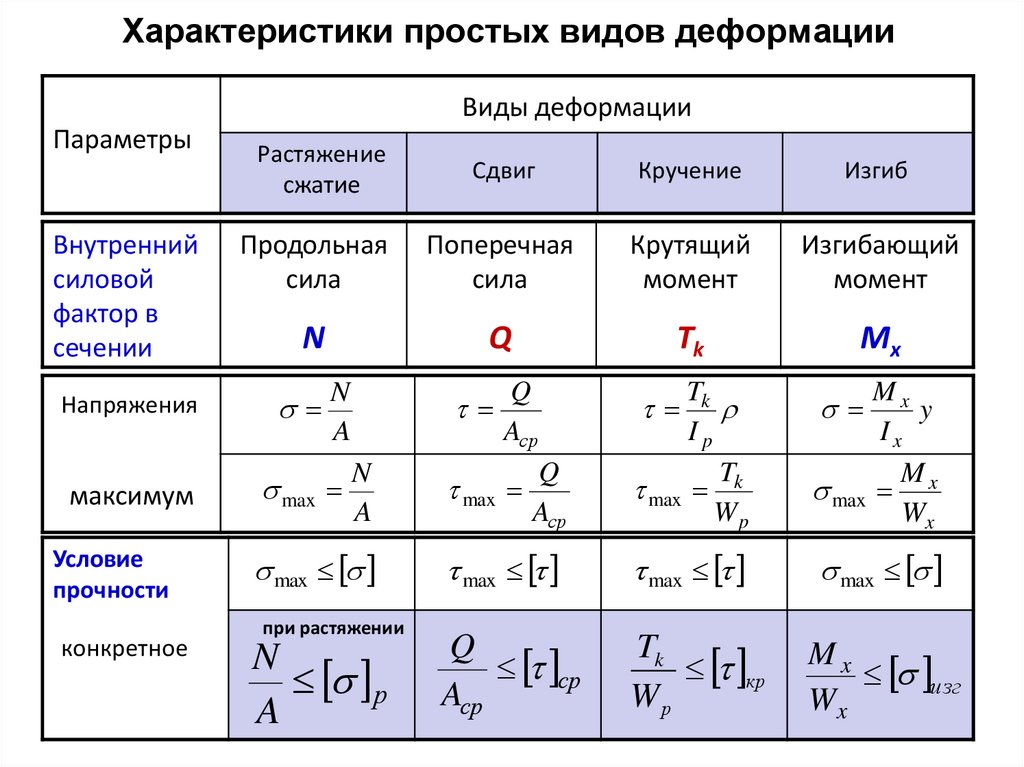
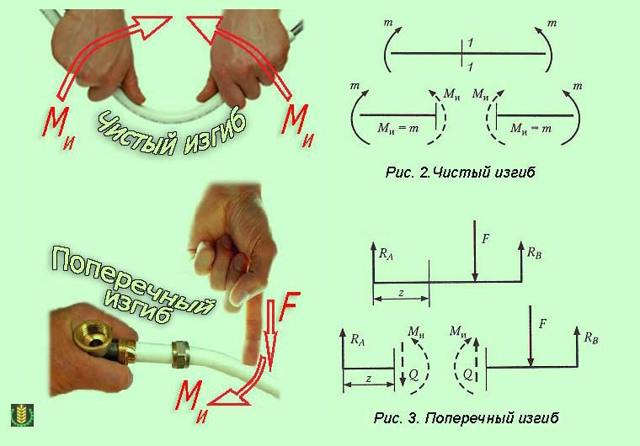
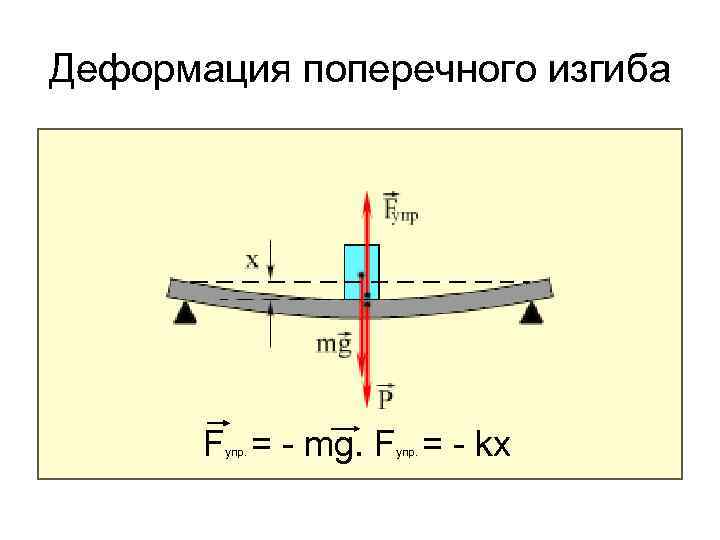
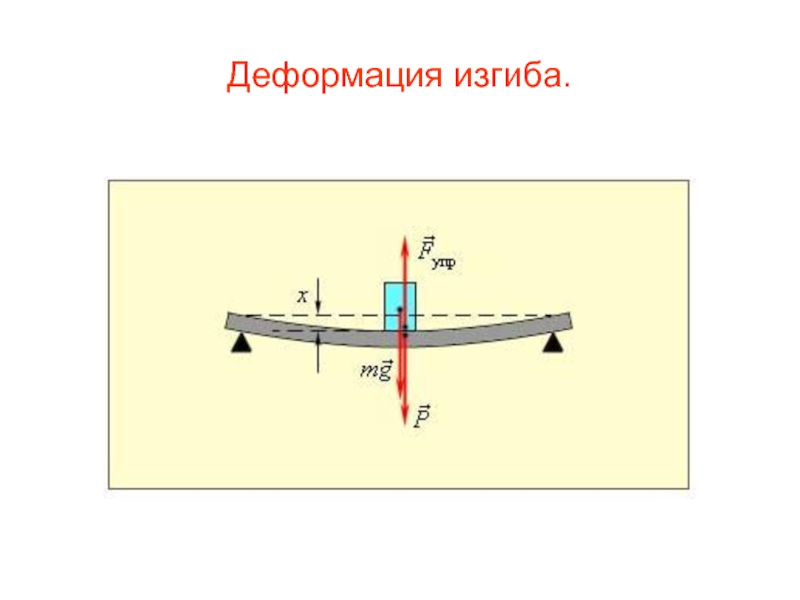
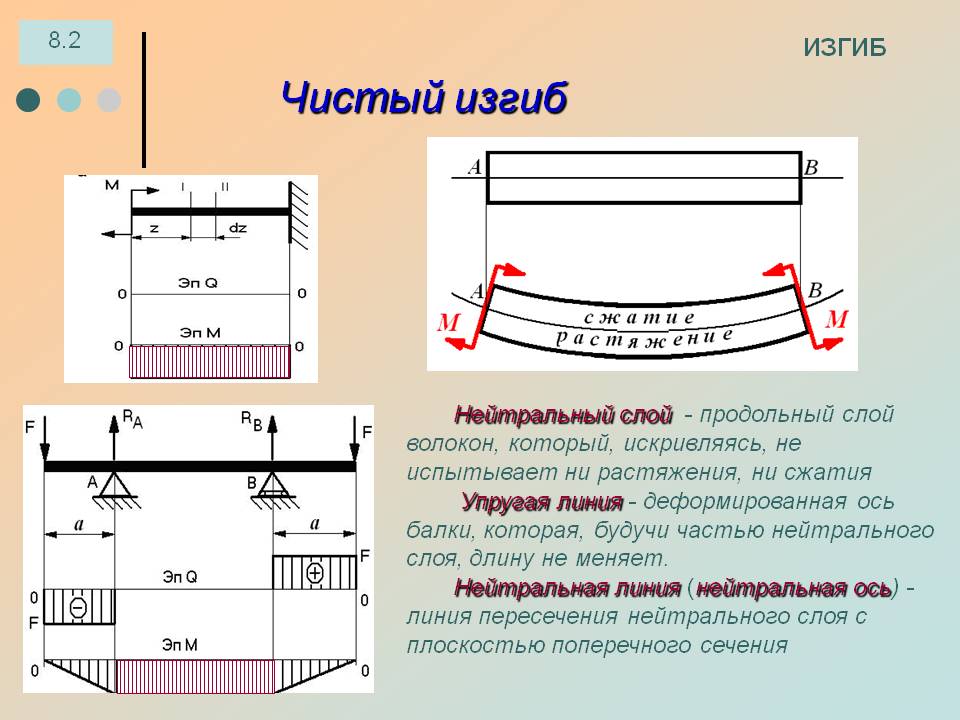
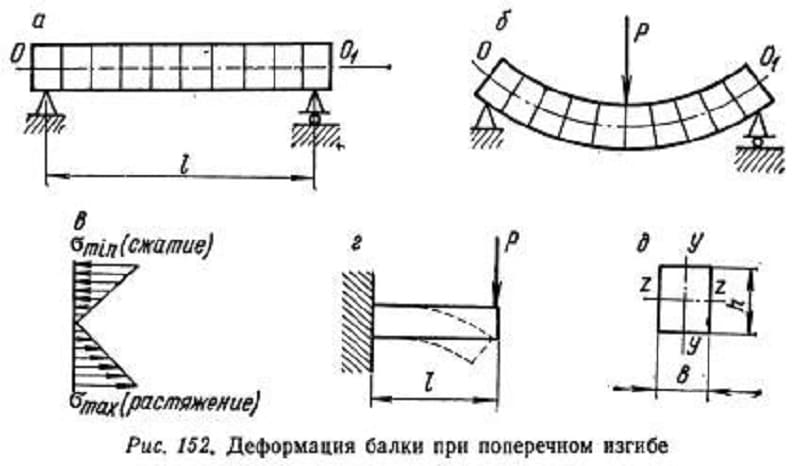
Внутренние силовые факторы при изгибе балки.

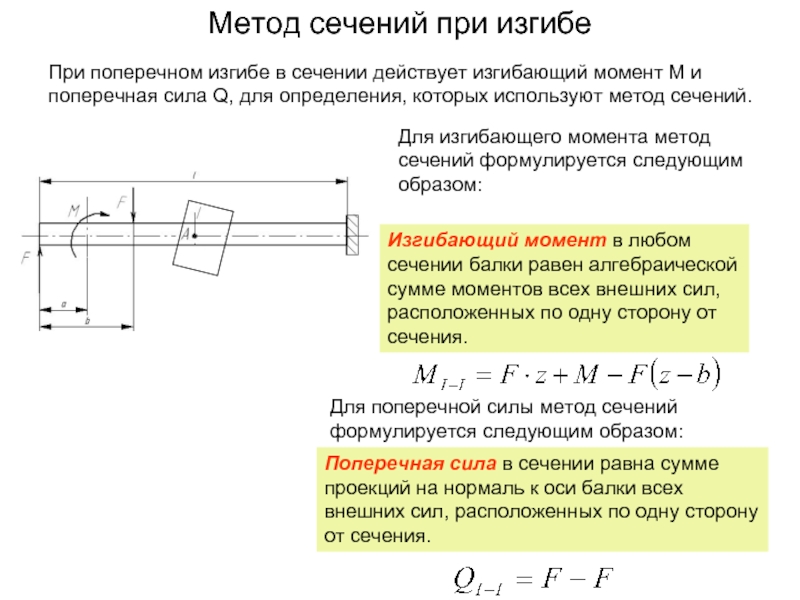
При плоском поперечном изгибе в сечениях балки возникают два внутренних силовых фактора: поперечная сила Q и изгибающий момент М. Для их определения используют метод сечений (см. лекцию 1). Поперечная сила Q в сечении балки равна алгебраической сумме проекций на плоскость сечения всех внешних сил, действующих по одну сторону от рассматриваемого сечения.

Правило знаков для поперечных сил Q:

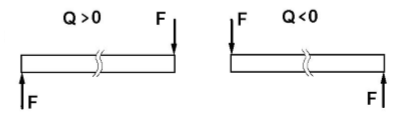
Изгибающий момент М в сечении балки равен алгебраической сумме моментов относительно центра тяжести этого сечения всех внешних сил, действующих по одну сторону от рассматриваемого сечения.

Правило знаков для изгибающих моментов M:

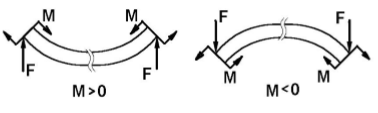
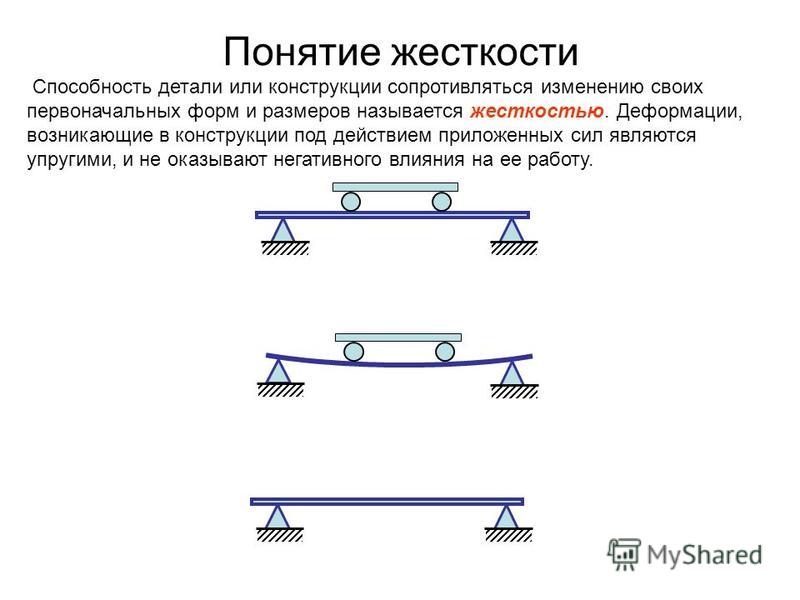
Расчеты на прочность и жесткость

Прочность характеризует способность конструкционного материала сопротивляться внешним воздействиям без разрушений и остаточных изменений. Жесткость находится в линейной зависимости от модуля Юнга и размера сечения. Чем больше площадь, модуль упругости не меняется, тем больше жесткость. В общем случае жесткость подразумевает способность деформироваться без значительных изменений. Коэффициент запаса прочности – безразмерная величина, равная отношению предельного напряжения к допустимому. Запас прочности характеризует штатный режим работы конструкции даже с учетом случайных и не предусмотренных нагрузок. Наименьшим запасом прочности обладают пластические (1.2-2.5) и хрупкие (2-5) материалы.

Применение в расчетах этих коэффициентов позволяет, например, рассчитать опасную толщину для стержня, при которой может возникнуть максимальное нормальное напряжение. Используя коэффициент прочности и возможное предельное напряжение возможно произвести расчет необходимого диаметра вала, который гарантированно обеспечит упругую деформацию и не приведет к пластической. Для инженеров-экономистов важны расчеты наименьших безопасных размеров деталей конструкции по заданным нагрузкам.

Большинство практических расчетов на прочность и жесткость производятся для получения минимальных значений геометрических размеров конструкционных элементов и деталей машин в условиях известных внешних воздействий и необходимого и достаточного запаса прочности. Может решаться обратная задача получения значений предельных нагрузок при условии сохранения геометрических размеров и для конкретного материала.

Сложные конструкции могут быть разделены на элементарные части, для которых будут производиться расчеты, затем полученные результаты интерпретируются в рамках всей системы, для этого удобно строить эпюры распределения внешних воздействий и внутренних напряжений статически определенной системы.

С помощью известной жесткости материала делают расчеты максимально возможной длины балки или стержня (вала) при условии неизменности его сечения. Для ступенчатых валов необходимо строить эпюры воздействия внешних сил и возникающих в точках их приложения внутренних напряжений в критических точках. От правильно построенной теоретической модели будет зависеть насколько эффективно и долго прослужит вал для станка, не разрушится ли он от динамических крутящих моментов. На этапе проектирования можно выявить потенциальные слабые точки и рассчитать необходимые параметры для заданного предела прочности.

При расчетах соединений используют пределы текучести используемых материалов и коэффициенты запаса прочности, вычисляют максимально возможные напряжения.

Исследования на прочность обычно подразумевают решение нескольких задач: в условиях проведения поверочного расчета на проверку прочности при известных усилиях и площади сечения оценивают фактический коэффициент запаса прочности; подбор оптимального диаметра при заданных нагрузках и допустимом напряжении; вычисляют грузоподъемность или несущую способность с помощью определения внутреннего усилия при известной площади сечения и напряжении.

Прочностные расчеты при разных видах воздействий в рамках условно статических систем сложны, требуют учета многих, иногда не очевидных, факторов, их практическая ценность заключается в вычислении допустимых размеров конструкционных материалов для заданных параметров запаса прочности.

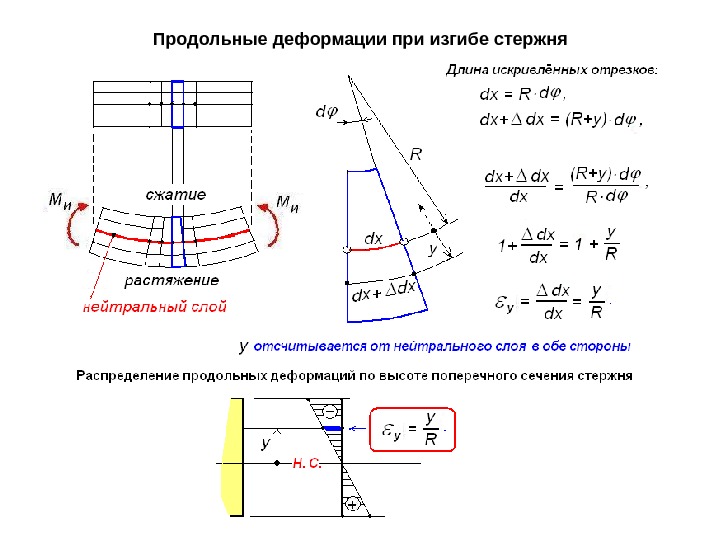
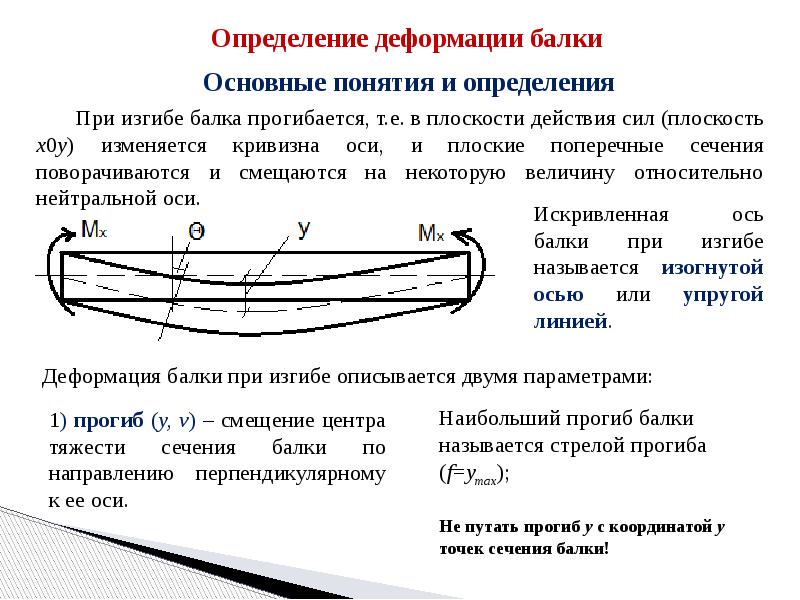
Перемещения при изгибе.

Под действием нагрузки при изгибе ось балки искривляется. При этом наблюдается растяжение волокон на выпуклой и сжатие – на вогнутой частях балки. Кроме того, происходит вертикальное перемещение центров тяжести поперечных сечений и их поворот относительно нейтральной оси. Для характеристики деформации при изгибе используют следующие понятия:

Прогиб балки Y – перемещение центра тяжести поперечного сечения балки в направлении, перпендикулярном к ее оси.

Прогиб считают положительным, если перемещение центра тяжести происходит вверх. Величина прогиба меняется по длине балки, т.е. y = y (z)

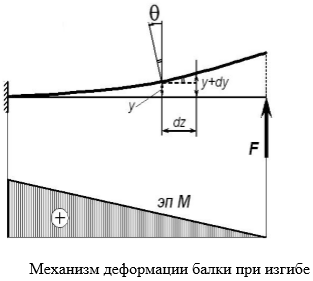
Угол поворота сечения – угол θ, на который каждое сечение поворачивается по отношению к своему первоначальному положению. Угол поворота считают положительным при повороте сечения против хода часовой стрелки. Величина угла поворота меняется по длине балки, являясь функцией θ = θ (z).

Самыми распространёнными способами определения перемещений является метод Мора и правило Верещагина.

Механическое напряжение

Определение 4

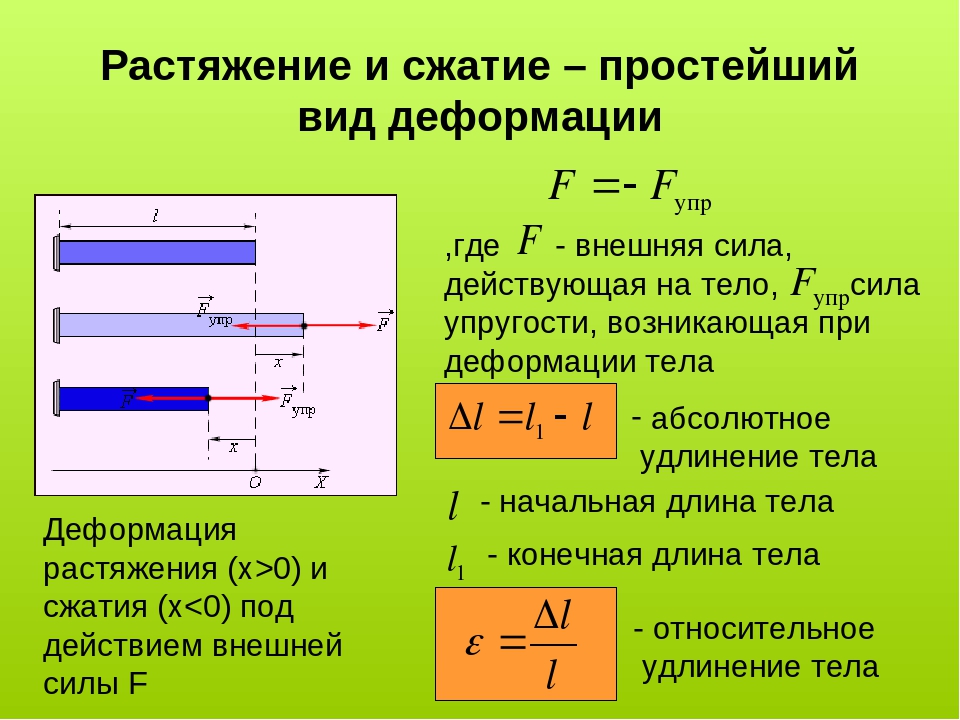
Механическое напряжение твердого тела σ – это показатель, равный отношению модуля внешней силы к площади сечения твердого тела.

σ=FS.

Величину механического напряжения принято выражать в паскалях (Па) и измерять в единицах давления.

Важно понимать, как именно механическое напряжение и относительная деформация связаны между собой. Если отобразить их взаимоотношения графически, мы получим так называемую диаграмму растяжения. При этом нам нужно отмерить величину относительной деформации по оси x, а механическое напряжение – по оси y

На рисунке ниже представлена диаграмма растяжения, типичная для меди, мягкого железа и некоторых других металлов

При этом нам нужно отмерить величину относительной деформации по оси x, а механическое напряжение – по оси y. На рисунке ниже представлена диаграмма растяжения, типичная для меди, мягкого железа и некоторых других металлов.

Рисунок 3.7.2. Типичная диаграмма растяжения для пластичного материала. Голубая полоса – область упругих деформаций.

В тех случаях, когда деформация твердого тела меньше 1% (малая деформация), то связь между относительным удлинением и механическим напряжением приобретает линейный характер. На графике это показано на участке Oa. Если напряжение снять, то деформация исчезнет.

Определение 5

Деформация, исчезающая при снятии напряжения, называется упругой.

Линейный характер связи сохраняется до определенного предела. На графике он обозначен точкой a.

Определение 6

Предел пропорциональности – это наибольшее значение σ=σпр, при котором сохраняется линейная связь между показателями σ и ε.

Слишком сложно? Не парься, мы поможем разобраться и подарим скидку 10% на любую работу

Опиши задание

На данном участке будет выполняться закон Гука:

ε=1Eσ.

В формуле содержится так называемый модуль Юнга, обозначенный буквой E.

Если мы продолжим увеличивать напряжение на твердое тело, то линейный характер связи нарушится. Это видно на участке ab. Сняв напряжение, мы также увидим практически полное исчезновение деформации, то есть восстановление формы и размеров тела.

Основные понятия

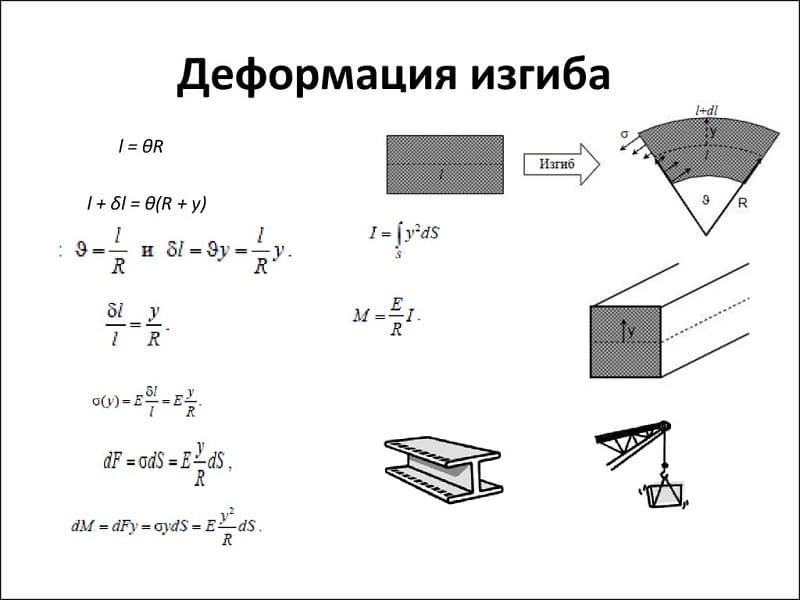
Под изгибом детали понимают естественное или искусственное изменение формы. Этот процесс разделяется на две категории – плоский или косой. В первом случае ось детали сохраняет своё первоначальное положение, во втором происходит её изменение в горизонтальной или вертикальной плоскости.

Основным теоретическим положением, определяющим физические процессы, протекающие в результате изгиба, является закон Гука. Согласно ему величина деформации (изгиба), пропорциональна приложенной к этому телу силе. Для каждого из видов деформации разработан индивидуальный расчёт действующих характеристик.

Оценка степени влияния действующих факторов на деформацию осуществляется с помощью следующих показателей:

• площади поверхности подверженной деформации;
• длины детали;
• силы, воздействующие на конструкцию;
• модуль упругости (его абсолютный показатель);
• величина и характер изменения модуля длины в результате упругой деформации.

Одним из важных параметров считается потенциальная энергия деформации при изгибе. На основании этих параметров производят определение модуля Юнга. С его помощью рассчитывают скорость распространения продольной волны. Величина механического напряжения, при которой деформация тела всё ещё будет упругой, а сам объект способен восстановить первоначальную форму после снятия нагрузки, называется пределом упругости. При превышении допустимого значения этого параметра тело начнёт разрушаться. Этот предел называется прочностью. При оценке прочностных показателей применяют следующие предположения:

1. О постоянстве нормальных напряжений. Она определяет постоянство расстояний при возникновении напряжений изгиба.
2. Плоскости сечений. Оно называется гипотезой Бернулли. Сечения детали в спокойном положении находятся в плоском состоянии. После деформации они сохраняют первоначальную форму, но разворачиваются относительно некоторой линии. Она называется нейтральной осью.
3. Отсутствие давлений на боковые поверхности. Считается, что соседние волокна не оказывают давления друг на друга.

Перечисленные гипотезы позволяют оценить деформации сдвига и характер изгиба каждого слоя исследуемой детали. Это происходит в результате воздействия различных сил. Нагрузки вызывают деформацию изгиба в различных плоскостях. Они подразделяются на две категории:

• характеру воздействия (статические или динамические);
• степени воздействия (массовые или объёмные);
• поверхности (сосредоточенные, воздействуют на отдельные элементы поверхности и распределёнными – на всю поверхность).

К статическим относятся нагрузки, у которых место приложения и направления сил не меняется или изменяются медленно в течение определённого промежутка времени. К таким нагрузкам относится сила тяжести. В этом случае можно принять утверждение, что элементы физического объекта находятся в состоянии равновесия. У динамических нагрузок эти параметры меняются достаточно быстро или носят импульсивный характер. К ним относятся ударные нагрузки при забивании свай, обработке металла ковкой, воздействие неровностей дороги на колесо.

При сосредоточенной статической нагрузке на отдельный участок поверхности бруса происходит его деформация в сторону по направлению сил взаимодействия. Для расчёта параметров характеризующих основные показатели состояния деформированного тела применяют дифференциальные уравнения, которые позволяют выявить существующие функциональные связи. По деформации изгиба с помощью модуля Юнга можно вычислить прочность исследуемого элемента конструкции (балки, бруса, подвесной опоры и т. д.). На основании полученных областей решения можно построить графическое изображение силы упругости, которое наглядно показывает, что происходит с различными участками деформированной детали. Для каждой детали в зависимости от её геометрических размеров, материала изготовления и величины приложенных сил выведена своя формула.

Для наглядности восприятия характера протекающих процессов использует метод нанесения эпюр на поверхность объекта. Эта операция называется топология. Основной идеей является проецирование линий нагрузки на соответствующую плоскость (горизонтальную, фронтальную или профильную). В современных методах топологии применяют фрактальную геометрию.

Рекомендуемые файлы

FREE

Учебный план для ИУ3, ИУ4, ИУ5, ИУ6, ИУ7, РК 6, РЛ6, МТ4, МТ8, МТ11, СМ13
Физика
FREE

Лекции 2, 6, 8 и 17 Юрасова Н. И.
Физика

Ф-65
Физика

М-61
Физика

6.1.16
Физика

6.2.13
Физика

Опора допускает вращение, но устраняет поступательное движение. Возникшую реакцию можно разложить на две составляющие ¾ горизонтальную и вертикальную.

3. Жесткая заделка.

Такое крепление не допускает ни линейных, ни угловых перемещений. Реакция, возникающая раскладывается на вертикальную и горизонтальную и момент защемления (реактивный момент).

7.2. Определение внутренних усилий при изгибе. Правило знаков для изгибающих моментов и поперечных сил.

Для определения внутренних усилий при изгибе (изгибающий момент и поперечная сила) применим метод сечений.

Рассмотрим равновесие левой части.

Взаимодействие внутренних частей заменим внутренними усилиями: изгибающим моментом M_и и поперечной силой Q. Для их определения используем два уравнения равновесия.

1) SY=0; A-F₁+Q=0; Q=S(F_i)_y

2) SM=0; A_z-F₁(Z-Q)-M_и=0

      M_и=Sm(F_c)

Таким образом:

1) Поперечная сила Q в поперечном сечении балки численно равна алгебраической сумме проекций на плоскость сечения всех внешних сил, действующих на одну сторону от сечения.

2) Изгибающий момент в поперечном сечении балки численно равен алгебраической сумме моментов (вычисленных относительно центра тяжести сечения) внешних сил, действующих по одну сторону от данного сечения.

Поперечная сила в сечении балки считается положительной; если равнодействующая внешних сил слева от сечения направлена снизу вверх, а справа сверху вниз, и отрицательной в противном случае.

Изгибающий момент в сечении mn балки считается

положителным, если равнодействующий момент внешних сил слева от сечения направлен по часовой стрелке, справа ¾ против. И отрицательным в противоположном случае.

Есть другое, более удобное для запоминания правило. Изгибающий момент положительный, если в рассматриваемом сечении балка изгибается выпуклостью вниз.

7.3. Построение эпюр изгибающих моментов и поперечных сил.

Рассмотрим пример:

Построить эпюры M_и и Q для балки на рис.

Проводим сечения Z₁ и Z₂. Изгибающий момент определим, взяв сумму моментов внешних сил справа от сечения

M_и=0

В сечении II-II

MZ₂=-F(Z₂ – a₂)

Знак минус потому что балка изгибается выпуклостью вверх.

Получили уравнение прямой

M_z2 = a₂ = 0

M_z2 = a₁ + a₂ = -F_a1                                          M_max=-F_a1 возникает у места заделки

Вычислим поперечную силу в сечении I-I. Проектируя на оси силы справа от сечения получим Q_z1=0. Тем же путем Q_z2=+F. Знак плюс взят т.к. внешняя сила справа от сечения направлена сверху вниз.

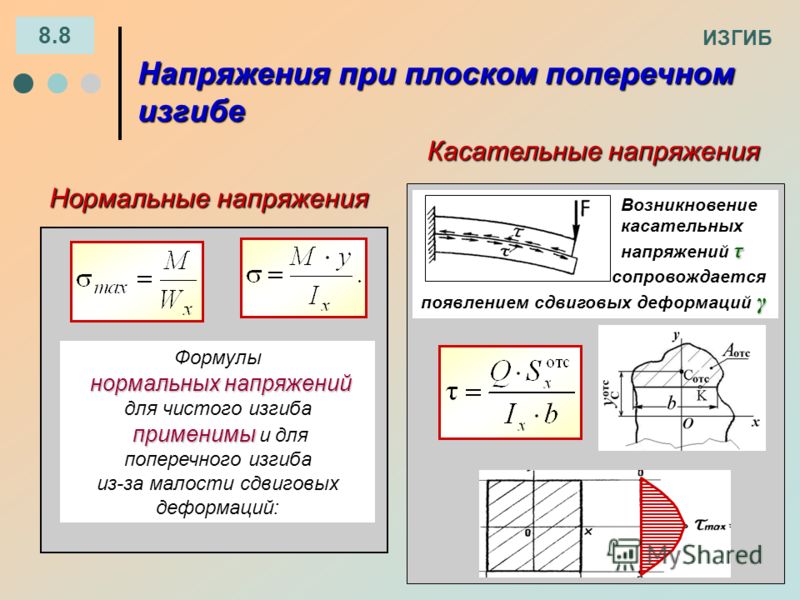
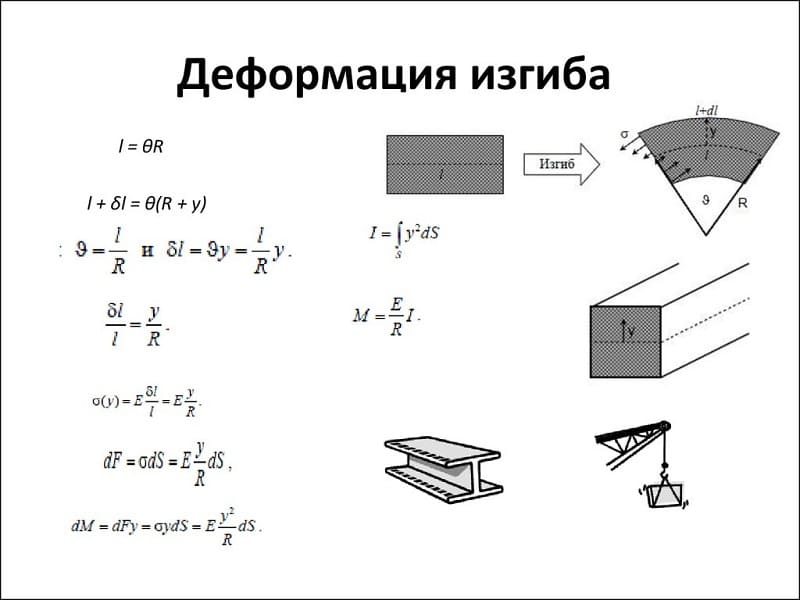
7.4. Определение нормальных напряжений. Условия прочности по нормальным напряжениям.

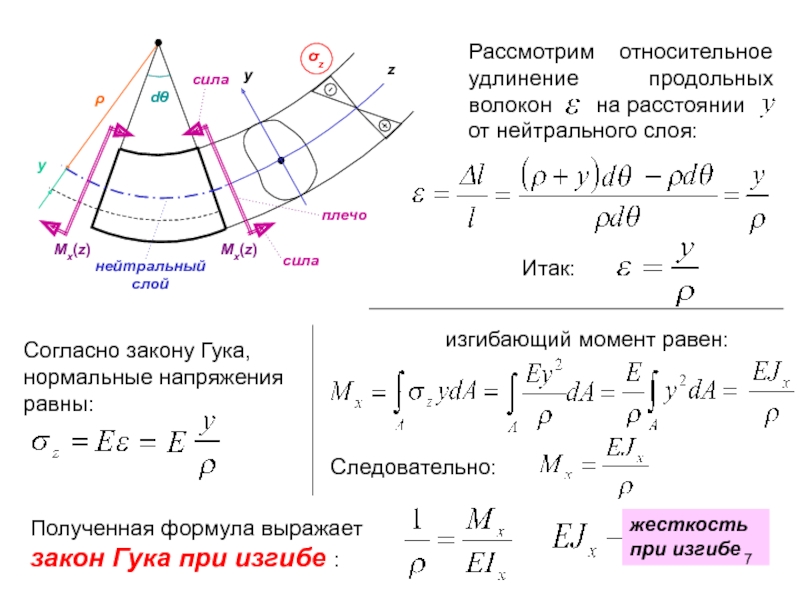
При деформации балки большие деформации испытывают более удаленные от нейтрального слой. Это слой, не испытывающий при изгибе ни растяжения ни сжатия.

Относительное удлинение волокна

e = Z / r

Z ¾ расстояние от нейтральной оси до рассматриваемого волокна.

r ¾ радиус кривизны нейтрального слоя

Тогда по закону Гука

s = Ee = E(Z / r)                     (1)

Можно также записать

M_и = EI_у / r,

где I_у = ò_AZ2dA ¾ представляет момент инерции сечения относительно нейтральной оси y. Откуда

1 / r = M_и / EI_у                                    (2)

K = 1 / r ¾ кривизна нейтрального слоя, т.е. кривизна оси балки при изгибе прямо пропорционально изгибающему моменту n и обратно пропорционально жесткости (Ei_у) балки. Подставляя (2) в (1) получим:

s = Z M_и / EI_у

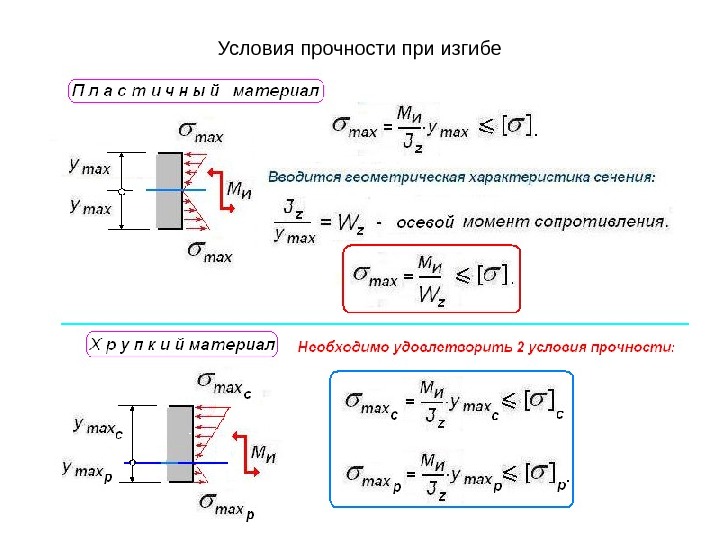
Для обеспечения прочности балки необходимо, чтобы наибольшие растягивающие и наибольшие сжимающие напряжения при исгибе в опасном сечении не превосходили допускаемых.

Обозначив h_р и  h_с ¾ расстояния до наиболее удаленных растянутого и сжатого волокна запишем:

max s_р = M_иh_р / EI_у

max s_с = M_иh_с / EI_у

Для хрупких материалов допускаемые напряжения [s_с] > [s_р] в 3-5 раз. Поэтому для балок применяют сечения не симметричные относительно нейтральной оси. В указанном случае надо составлять два условия прочности:

max s_р = M_и / W_ур £ [s_р]

max s_с = M_и / W_ус < [s_с]

при симметричном сечении балки

s = (M_и / I_у)(h / 2) £

W_у = 2I_у / h ¾ осевой момент сопротивления.

Момент сопротивления является геометричесой характеристикой поперечного сечения балки, определяющей прочность при изгибе.

Значения W_у для простейших случаев:

а) прямоугольник

W_x = 2I_x / h = bh2 / 6

б) круг

W_x = 2I_x / d = pd42 / 64d = pd3 / 32 » 0,1d3

в) для кольца

W_x = (pD3 / 32) / (1-c4) = 0,1D3(1-c4)

Допускаемый изгибающий момент определяется

[M_и] £ W_x

7.5. Рациональные формы сечения балок.

Рекомендация для Вас – 4.4. Контроль за выполнением производственной программы.

Для количественной оценки рациональности сечения (при замере материала) служит безразмерная величина

w_x = W_x / ÖA3

это осевой удельный момент сопротивления. w_x зависит только от формы сечения

круг w_x  = 0,14

двутавр w_x  = 1,02-1,51

Интенсивная пластическая деформация

Получить беспористые объемные металлические наноматериалы можно технологиями интенсивной пластической деформации (ИПД). Их суть заключается в деформировании металлических заготовок:

• при относительно небольших температурах;
• при повышенном давлении;
• с высокими степенями деформации.

Это обеспечивает формирование гомогенной наноструктуры с большеугловыми границами зерен. Вопреки интенсивному воздействию, образцы не должны получать механические повреждения и разрушаться.

Технологии ИПД:

1. кручение (ИПДК);
2. разноканальное угловое прессование;
3. всесторонняя ковка;
4. мультиосевое деформирование;
5. знакопеременный изгиб;
6. аккумулированная прокатка.

Первые работы по созданию наноматериалов выполнены в 80х-90х годах ХХ века с использованием методов кручения и разноканального прессования.  Первый метод применим для небольших образцов – получаются пластинки диаметром 10…20 мм и толщиной до 0,5 мм. Для того чтобы получить массивные наноконструкции используется второй метод, в основу которого положена деформация сдвигом.

Они высокопроизводительные, позволяют обеспечить требуемое качество получаемых изделий, улучшить их механические свойства.