Коэффициент жесткости пружины

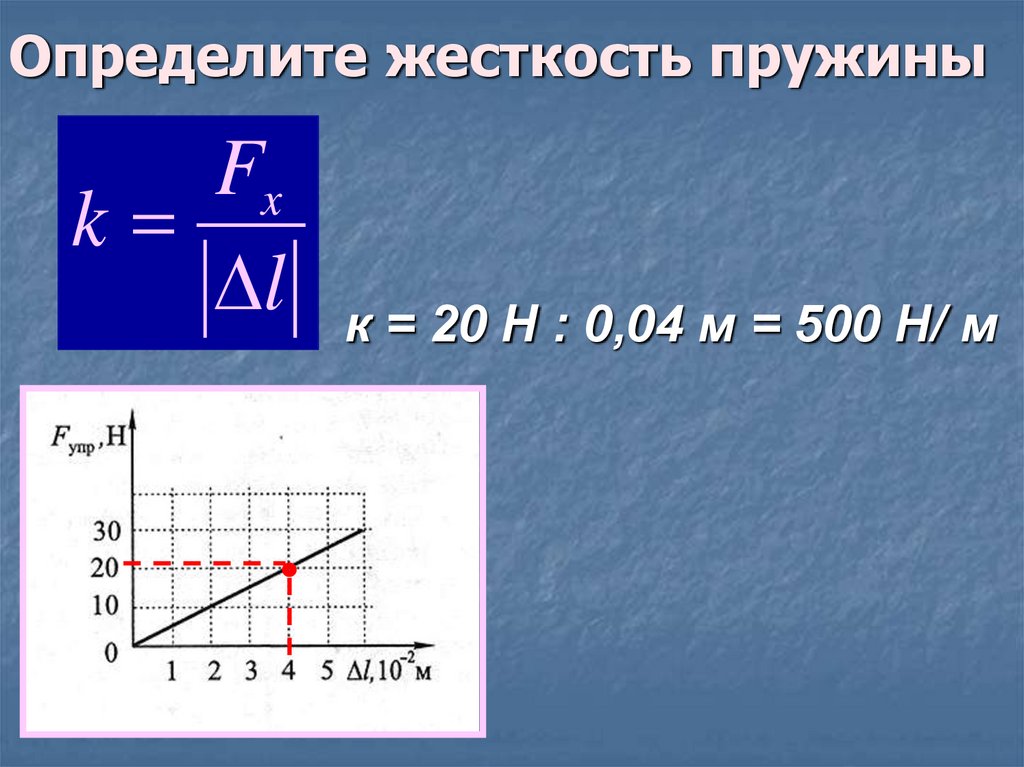
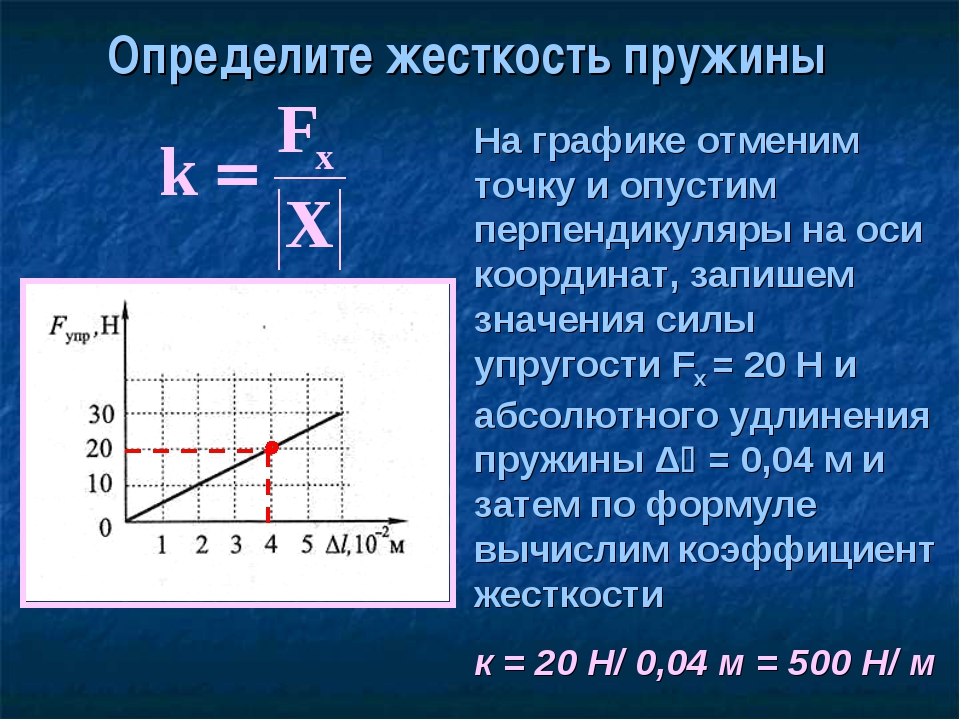
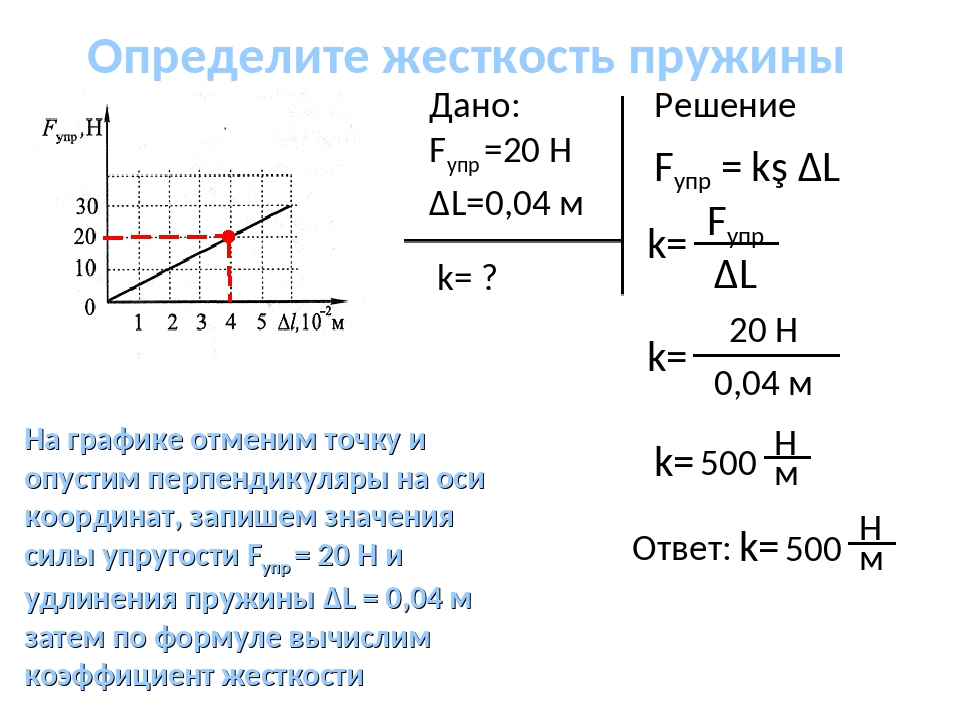
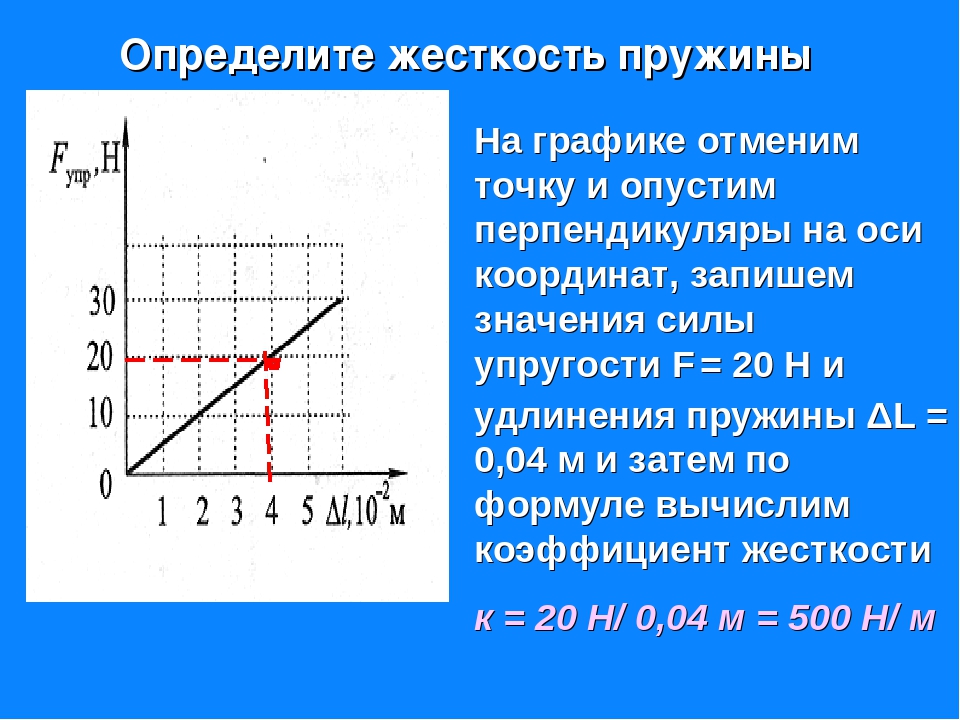
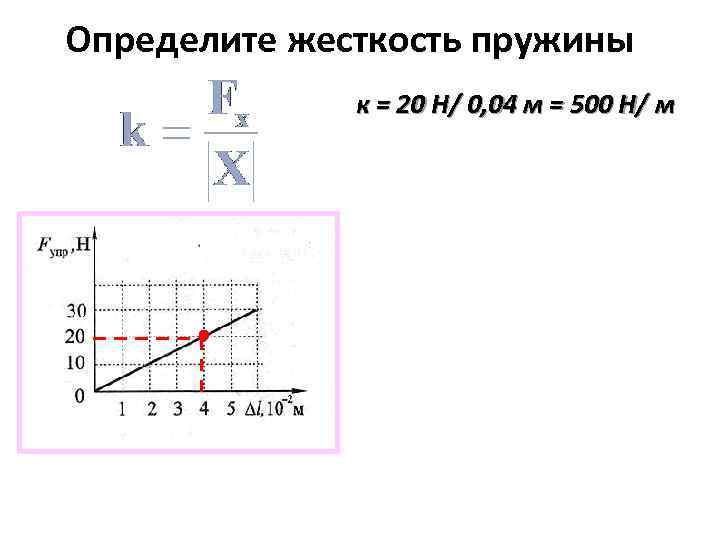
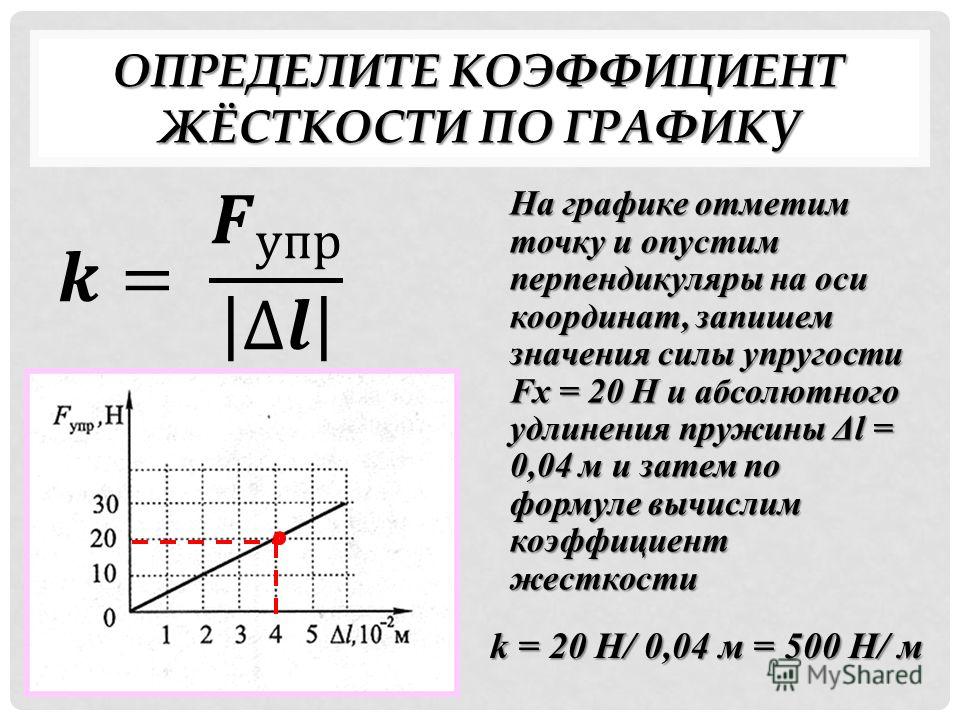
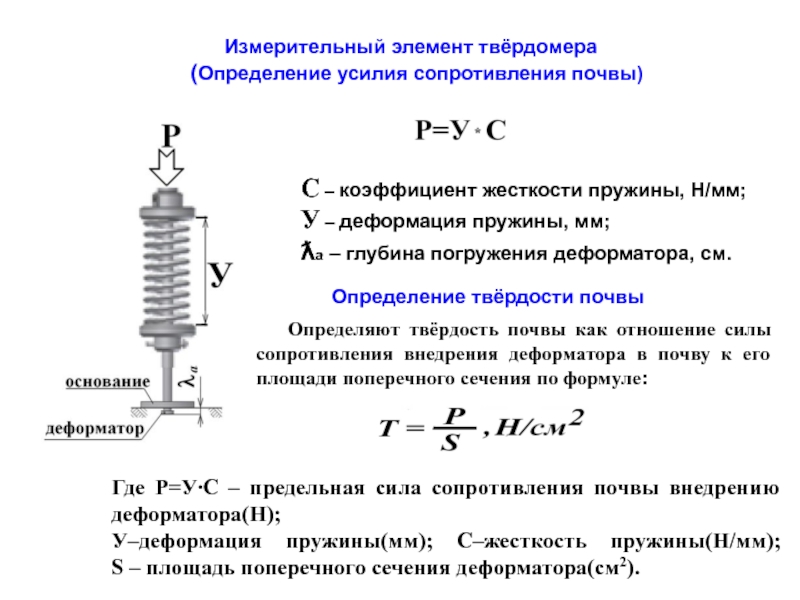
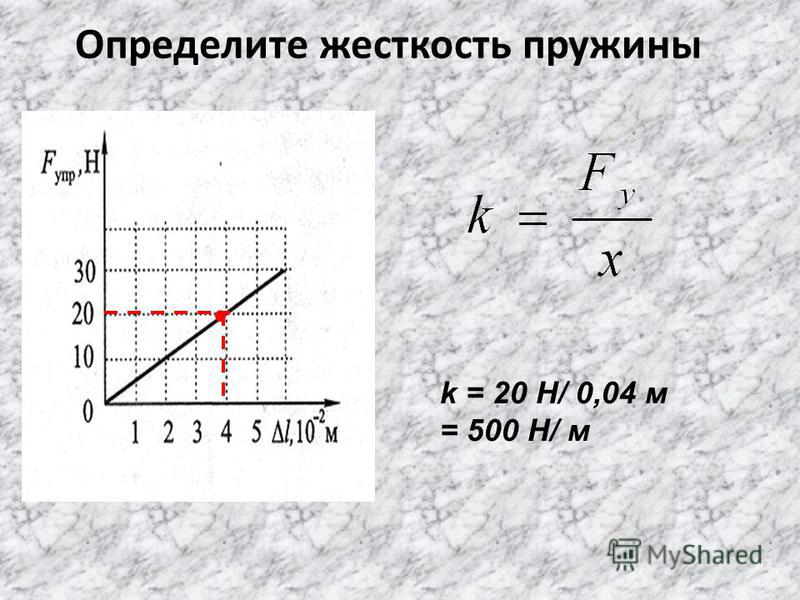
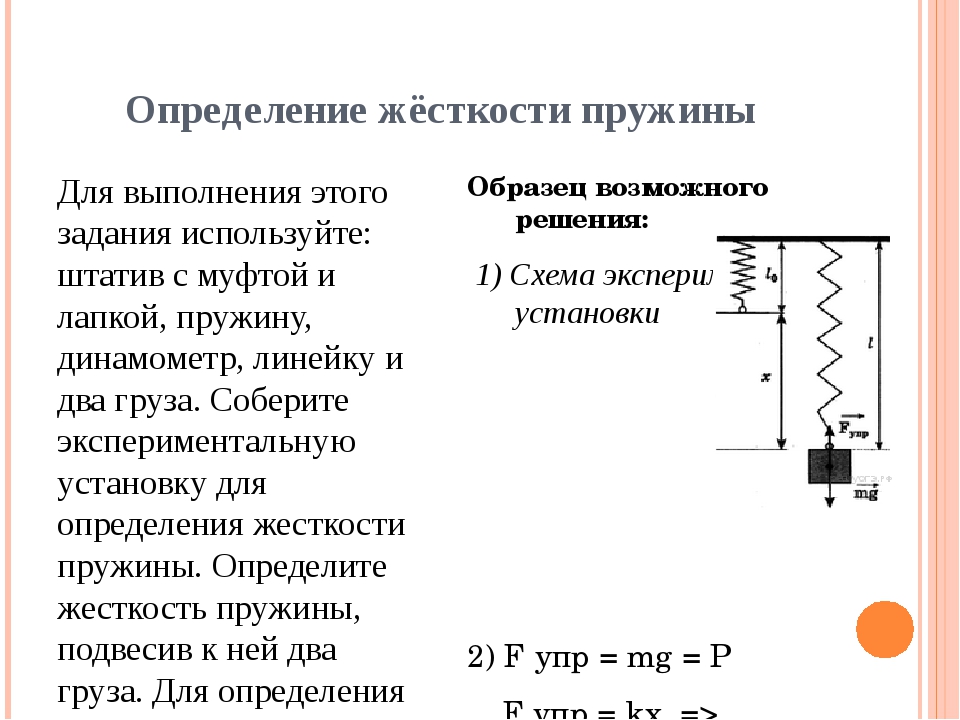
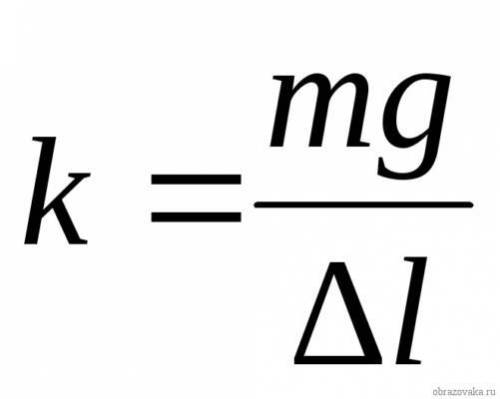Примеры решения задач

ПРИМЕР 1

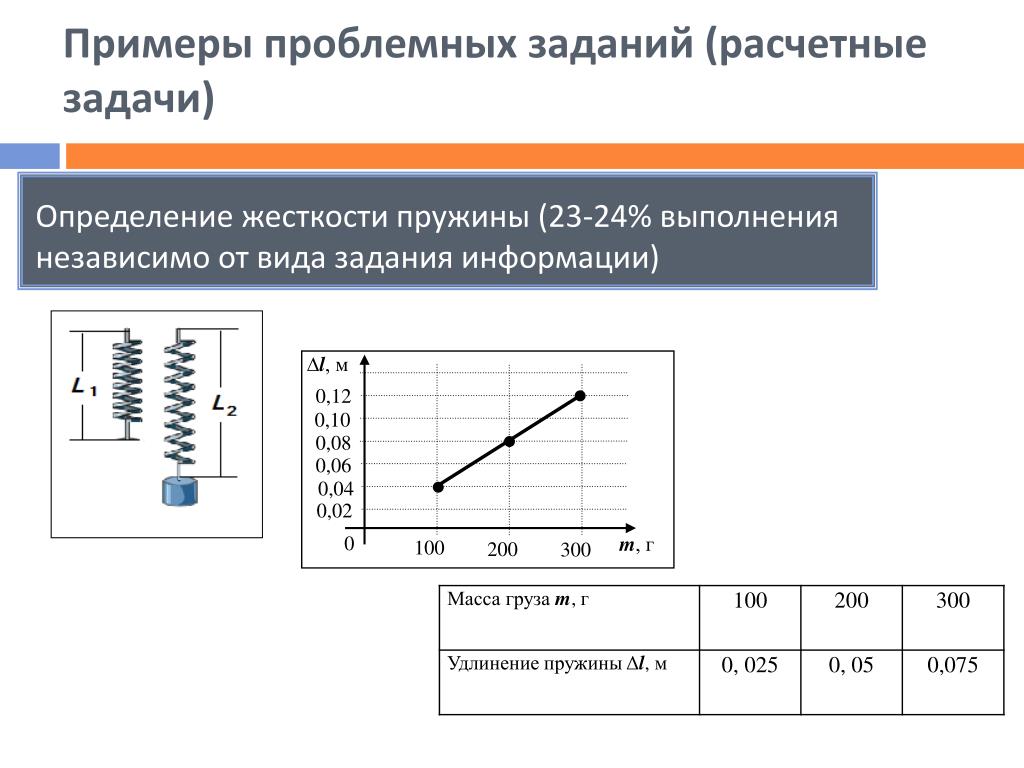
Задание	Какова работа, совершается при сжатии пружины на величину ? Считать, что сила упругости пропорциональна сжатию, коэффициент упругости пружины равен k.
Решение	В качестве основной формулы используем определение работы вида: Сила по условию пропорциональна величине сжатия, что математически можно представить как: Подставим выражения для силы (1.2) в формулу (1.1):
Ответ

ПРИМЕР 2

Задание	Вагон массой двигался со скоростью . Он ударился о стенку. При ударе каждый буфер вагона сжался на l м. Буферов два. Каковы коэффициенты упругости пружин, если считать, что они равны?
Решение	Сделаем рисунок.

ая энергия пружины?

___

потенциальная энергия пружины?

2. Тело, масса которого 5 кг, находится на высоте 12 м над поверхностью земли. Вычислите его потенциальную энергию:

а) относительно оверхности земли;

б) относительно крыши здания, высота которого 4 м.

___3. Недеформированную пружину динамометра растянули на 10 см, и ее потенциальная энергия стала 0,4 Дж. Каков коэффициент жесткости пружины?

100 Н, а ко второй, жесткостью k2, – 50 Н. Как соотносятся жесткости пружин?

делениями 0 и 1 его шкалы равно 2 см.

k=…………………..

каково значение силы тяжести действующей на груз

G=………………………….

3) для этого задания нужно полное решение нада определить вес астронавта массой 100кг сначала на луне а потом на марсе

4)надо определить обсалютное удлинение пружины жесткостью 50 Н/м если

на неё действуют с силой 1 н и б)к ней подвешено тело массой 20 г

5)астронавт находясь на лун подвесил к пружине деревянный брус массой 1кг. пружина удлинилась на два см. затем астронавт с помощью той же пружины равномерно тянул брус по горизонтальной поверхности. в этом случае пружина удлинилась на 1 см

надо определить

жесткость пружины…………………

величину силы трения…………..

во сколько раз сила трения могла быть больше если бы экспиримент проводился на марсе

плиз нужно через 4 часа я прошу вас

7. В случае уменьшения длины спиральной пружины на 3,5 см возникает сила упругости, равная 1,4 кН. Какой будет сила упругости пружины, если уменьшить ее длину на 2,1 см? 8. При открывании двери длина дверной пружины увеличилась на 0,12 м; сила упругости пружины составляет при этом 4 Н. За которого удлинения пружины сила упругости равна 10 Н? 9. Сила 30 Н растягивает пружину на 5 см. Какая сила растянет пружину на 8 см? 10. В результате растяжения недеформованої пружины длиной 88 мм, до 120 мм возникла сила упругости, равная 120 Н. Определите длину этой пружины в том случае, когда сила, действующая на нее, равна 90 Н. он находится в равновесии.

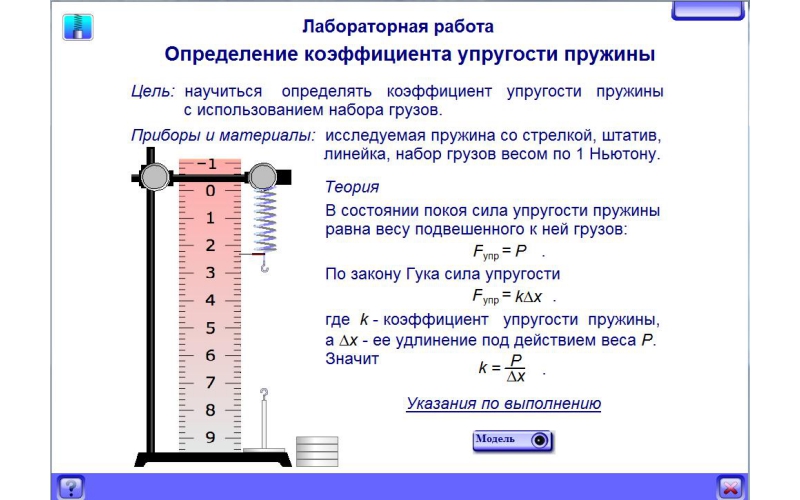
Формула жесткости пружины – едва ли не самый важный момент в теме об этих упругих элементах. Ведь именно жесткость играет очень важную роль в том, благодаря чему эти комплектующие используются так широко.

Сегодня без пружин не обходится практически ни одна отрасль промышленности, они используются в приборо- и станкостроении, сельском хозяйстве, производстве горно-шахтного и железнодорожного оборудования, энергетике, других отраслях. Они верой и правдой служат в самых ответственных и критических местах различных агрегатов, где требуются присущие им характеристики, в первую очередь жесткость пружины, формула которой в общем виде очень проста и знакома детям еще со школы.

Ход работы

II. Актуализация знаний.

• Что такое деформация?
• Сформулировать закон Гука
• Что такое жесткость и в каких единицах она измеряется.
• Дайте понятие об абсолютной и относительной погрешности.
• Причины, приводящие к появлению погрешностей.
• Погрешности, возникающие при измерениях.
• Как чертят графики результатов эксперимента.

Возможные ответы учащихся:

Деформация – изменение взаимного положения частиц тела, связанное с их перемещением относительно друг друга. Деформация представляет собой результат изменения межатомных расстояний и перегруппировки блоков атомов. Деформации разделяют на обратимые (упругие) и необратимые (пластические, ползучести). Упругие деформации исчезают после окончания действия приложенных сил, а необратимые — остаются. В основе упругих деформаций лежат обратимые смещения атомов металлов от положения равновесия; в основе пластических — необратимые перемещения атомов на значительные расстояния от исходных положений равновесия.

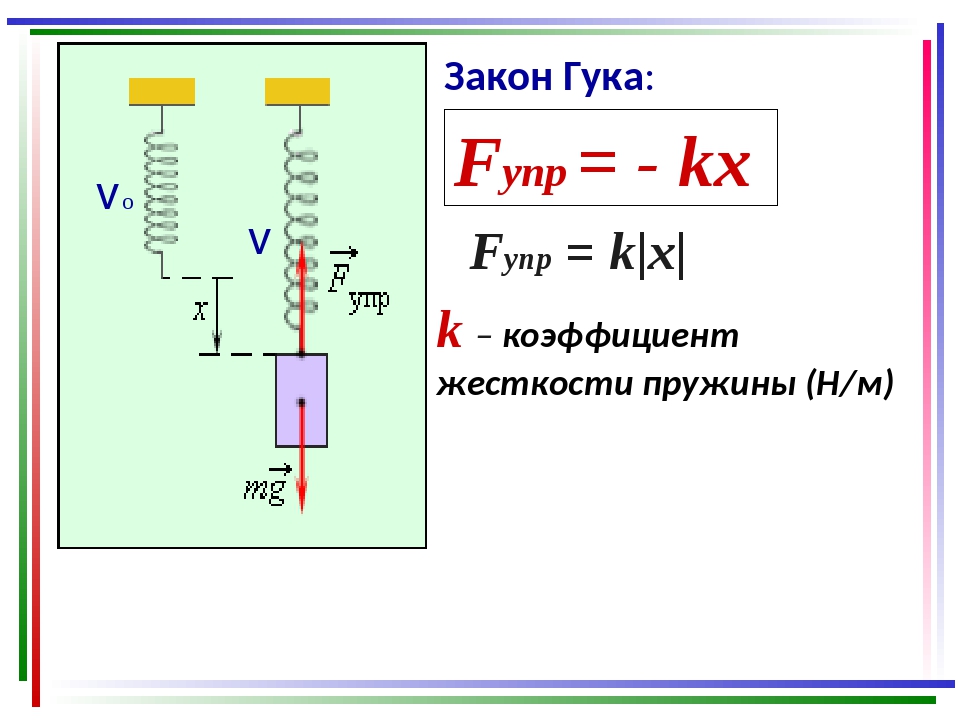
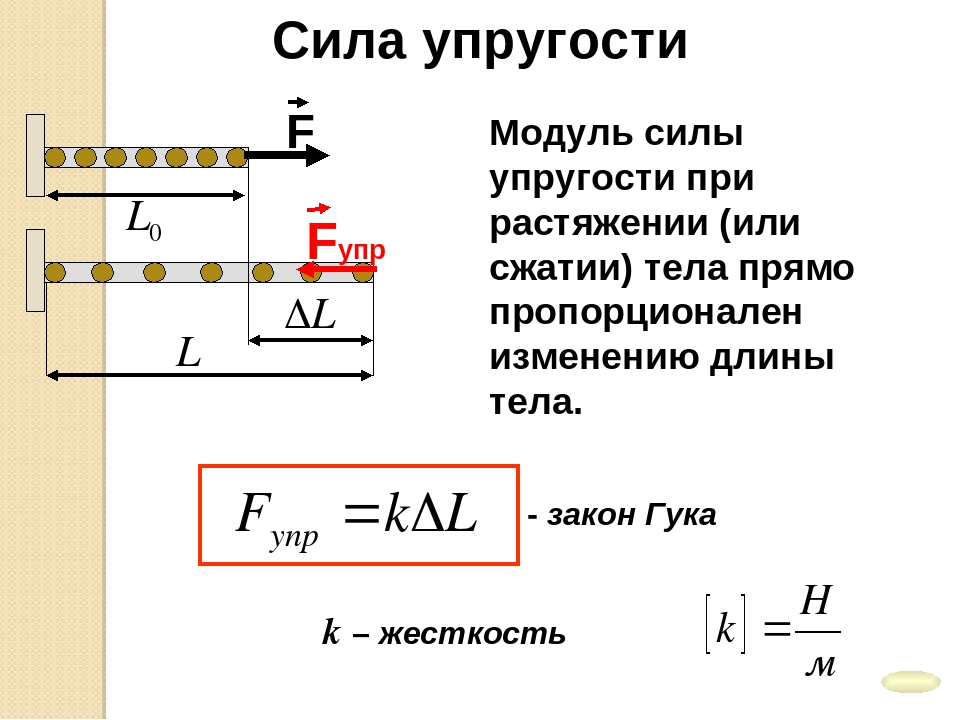
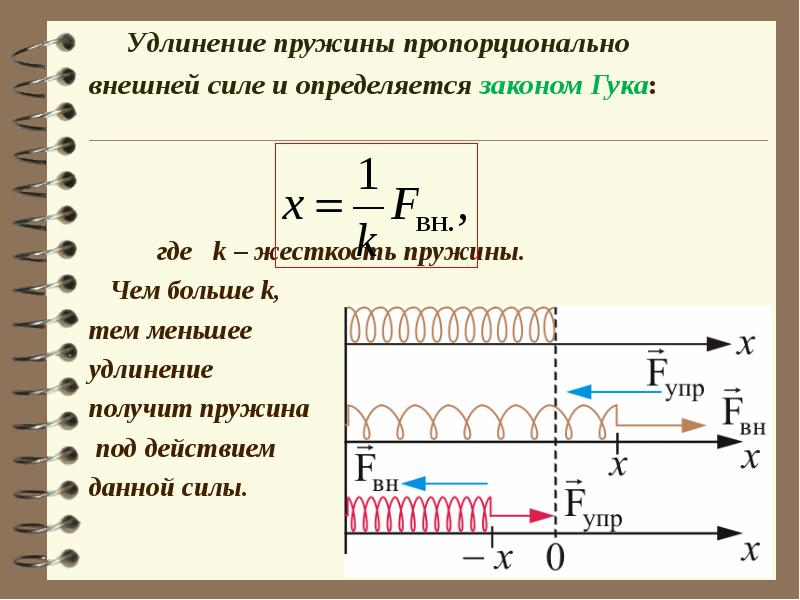
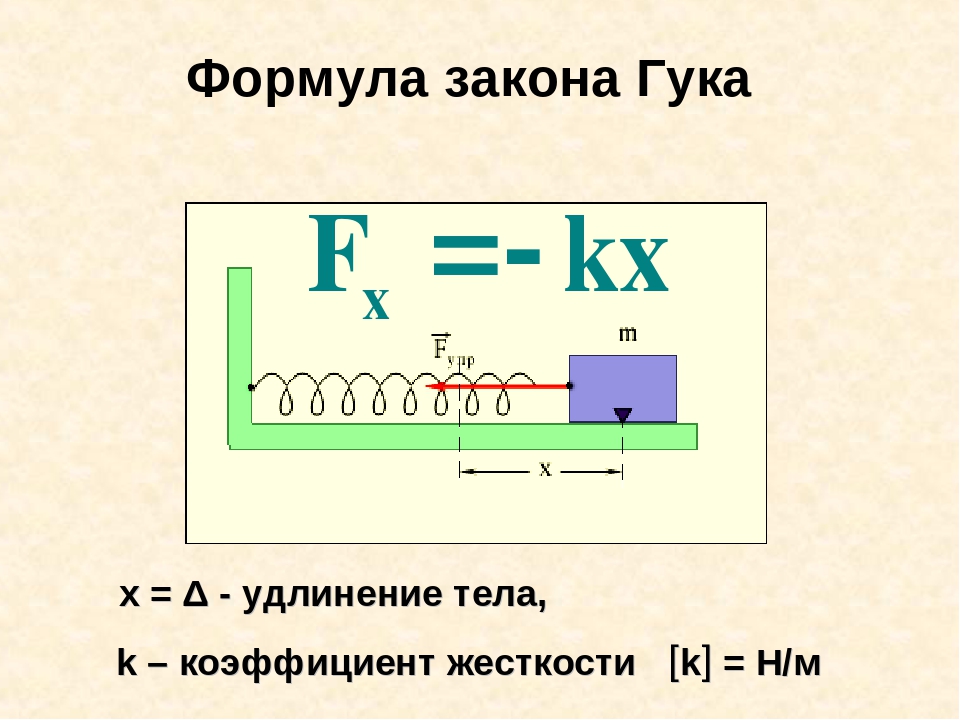
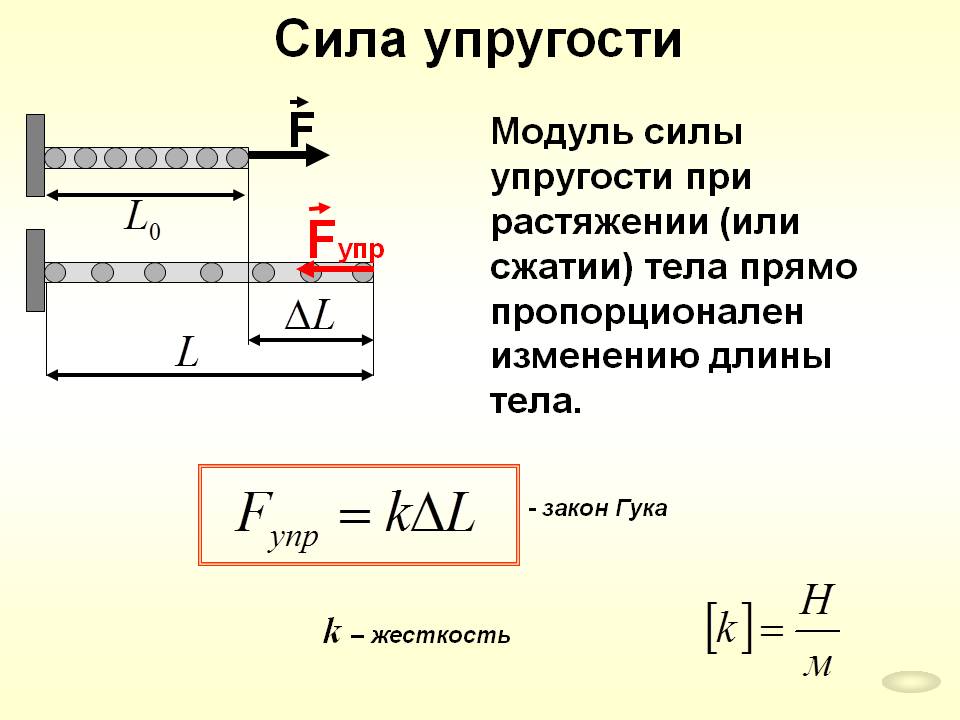
Закон Гука: «Сила упругости, возникающая при деформации тела, пропорциональна его удлинению и направлена противоположно направлению перемещения частиц тела при деформации». Fупр = –kx

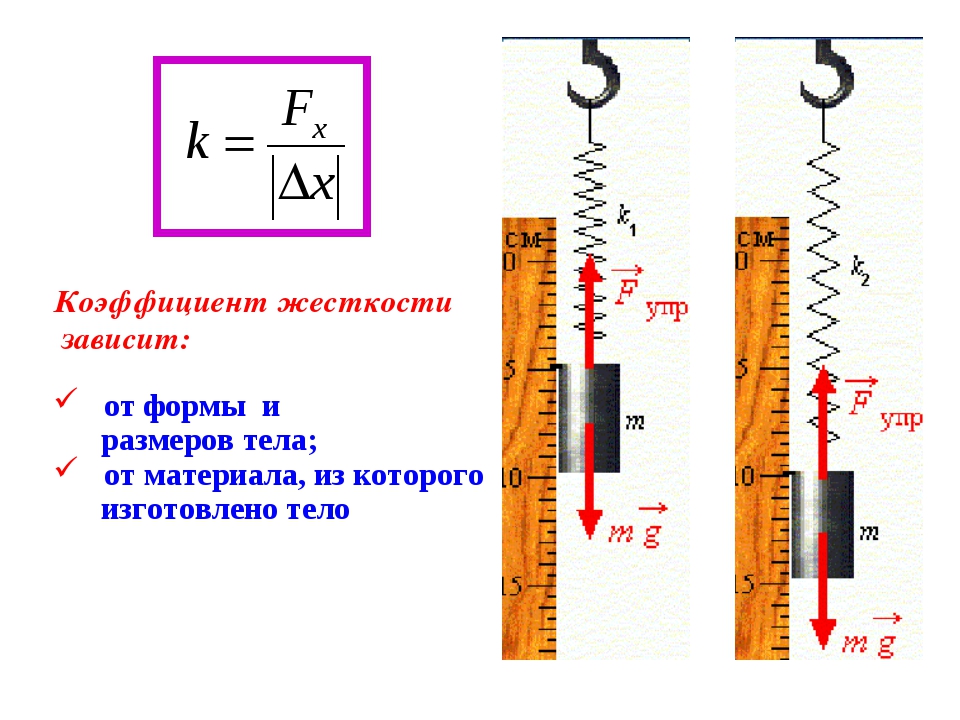
Жесткостью называют коэффициент пропорциональности между силой упругости и изменением длины пружины под действием приложенной к ней силы. Обозначают k. Единица измерения Н/м. Согласно третьему закону Ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. Таким образом жесткость пружины можно выразить как:
k = Fупр/x

Измерения никогда не могут быть выполнены абсолютно точно. Результат любого измерения приближенный и характеризуется погрешностью – отклонением измеренного значения физической величины от ее истинного значения. К причинам, приводящим к появлению погрешностей, относятся: – ограниченная точность изготовления средств измерения. – изменение внешних условий (изменение температуры, колебание напряжения) – действия экспериментатора (запаздывание с включением секундомера, различное положение глаза. ). – приближенный характер законов, используемых для нахождения измеряемых Величин

Погрешности, возникающие при измерениях, делятся на систематические и случайные. Систематические погрешности – это погрешности, соответствующие отклонению измеренного значения от истинного значения физической величины всегда в одну сторону (повышения или занижения). При повторных измерениях погрешность остается прежней. Причины возникновения систематических погрешностей: – несоответствие средств измерения эталону; – неправильная установка измерительных приборов (наклон, неуравновешенность); – несовпадение начальных показателей приборов с нулем и игнорирование поправок, которые в связи с этим возникают; – несоответствие измеряемого объекта с предположением о его свойствах.

Случайные погрешности – это погрешности, которые непредсказуемым образом меняют свое численное значение. Такие погрешности вызываются большим числом неконтролируемых причин, влияющих на процесс измерения (неровности на поверхности объекта, дуновение ветра, скачки напряжения и т.д.). Влияние случайных погрешностей может быть уменьшено при многократном повторении опыта.

Погрешности средств измерений. Эти погрешности называют еще инструментальными или приборными. Они обусловлены конструкцией измерительного прибора, точностью его изготовления и градуировки.

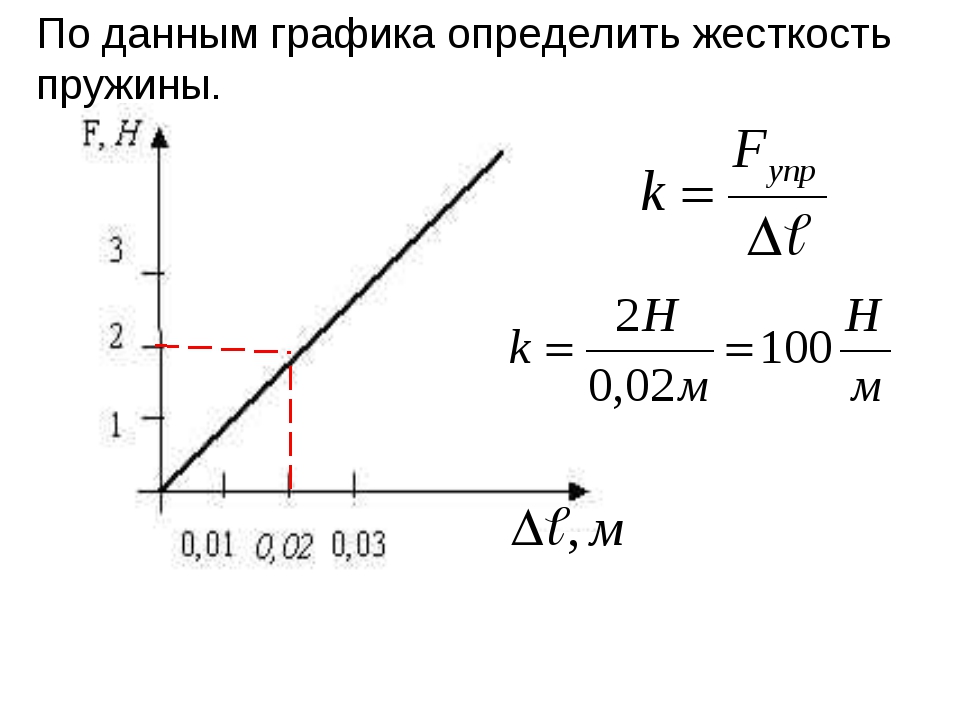
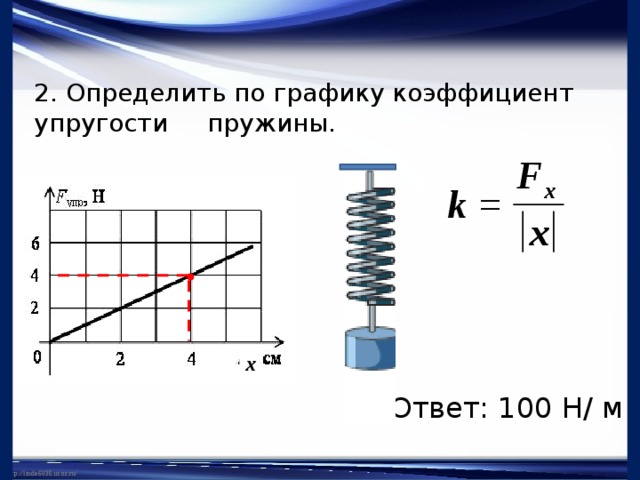
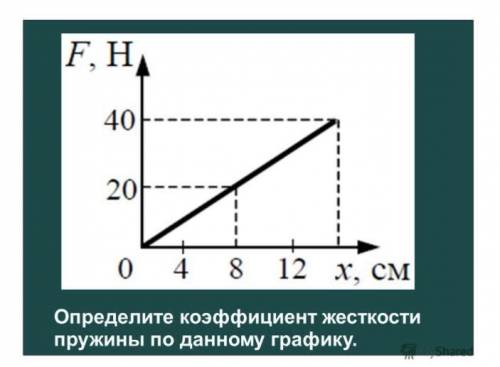
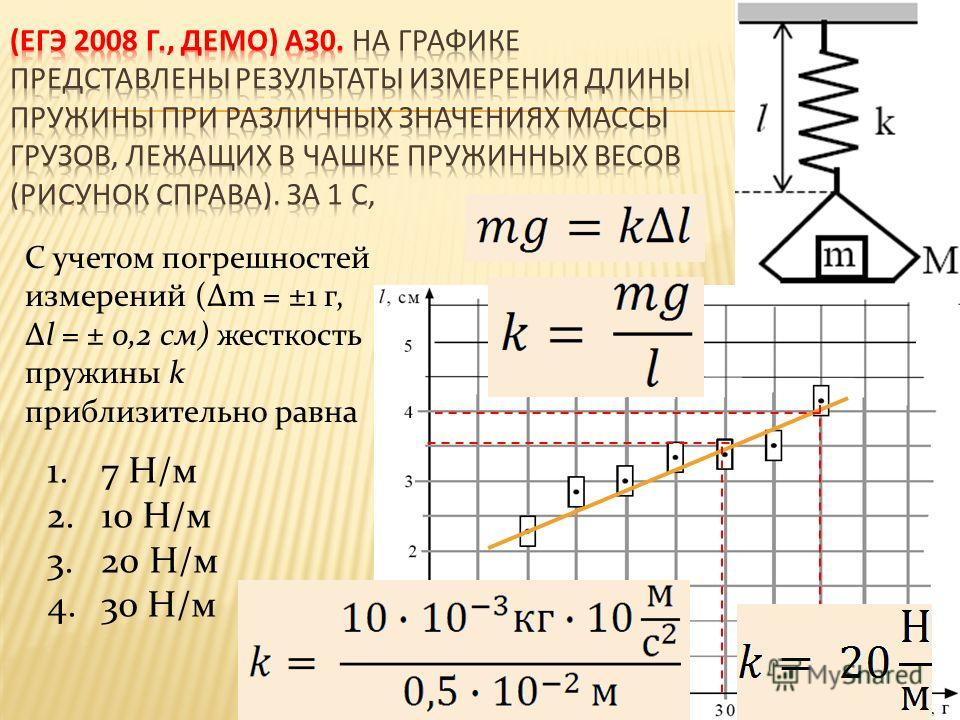
При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле F_упр = kx

Это связано с погрешностями измерения. В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k. Она и будет искомым средним значением жесткости пружины k_ср.

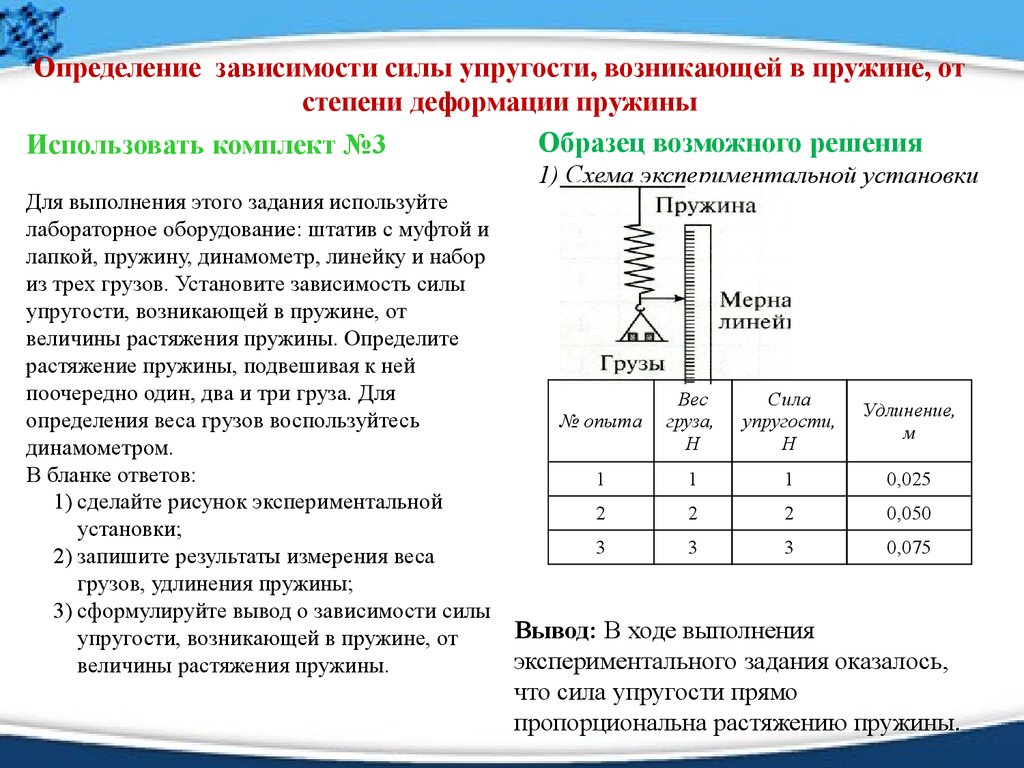
III. Порядок выполнения работы

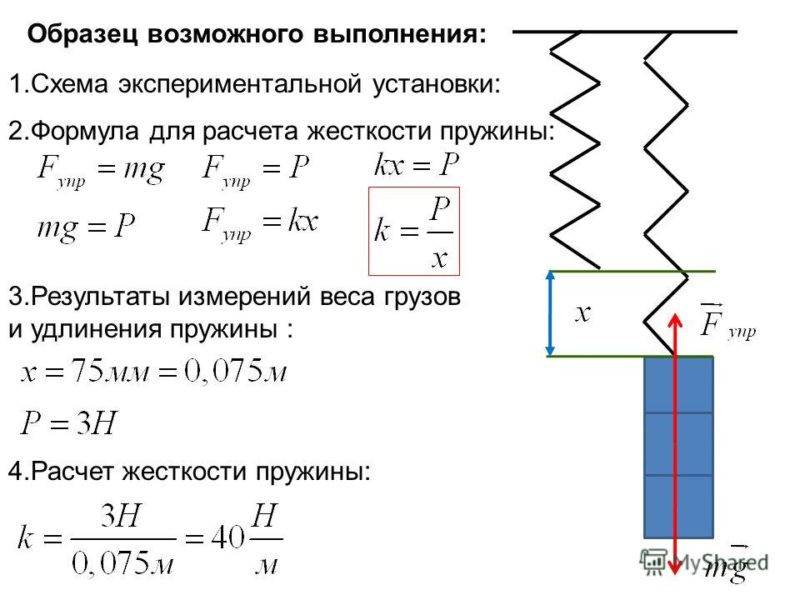
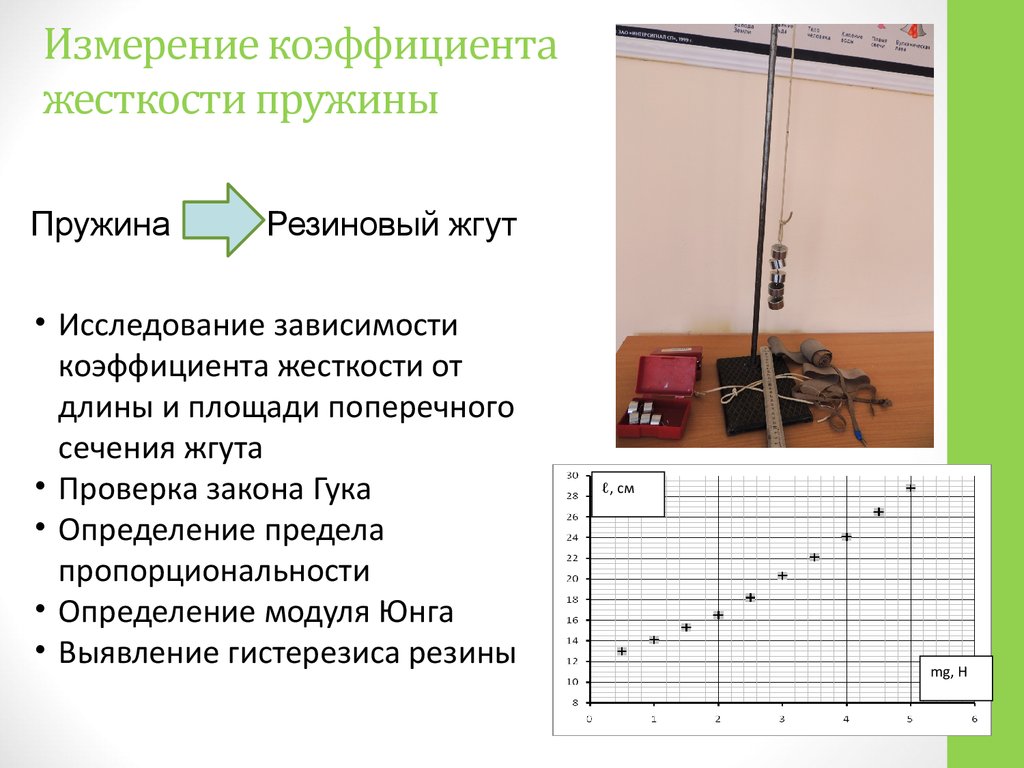
1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указателем и крючком см. рис.).

2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.

3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.

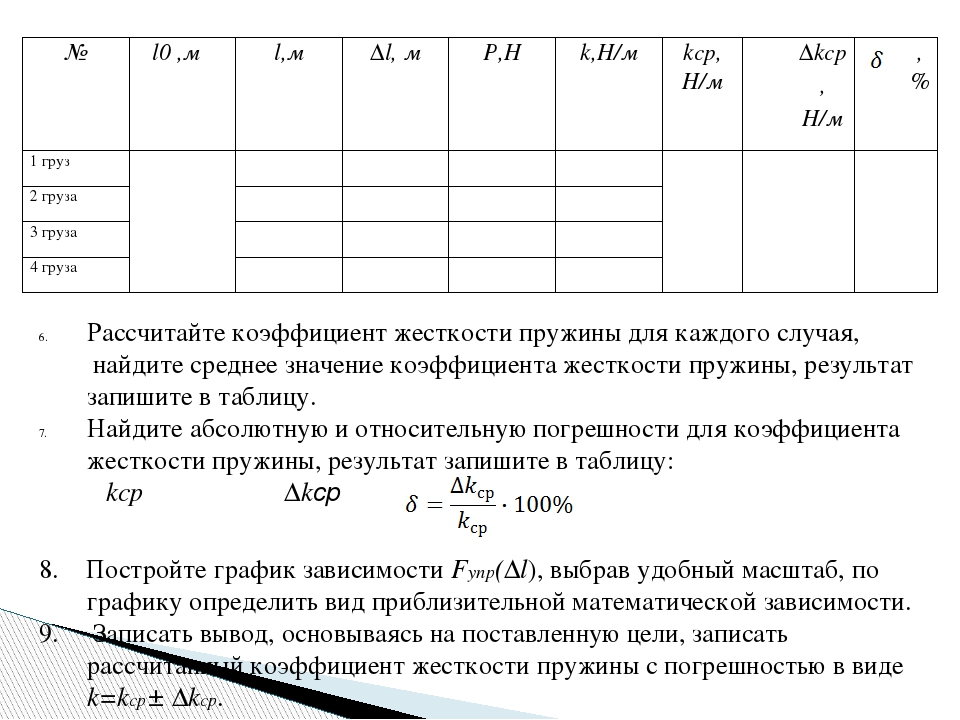
4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.

5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение |х| пружины.

По результатам измерений заполните таблицу:

Опытный метод

Чтобы понять, как найти жесткость пружины, а точнее, определить коэффициент жесткости пружины опытным путем, следует произвести следующие манипуляции. Вам необходимо деформировать тело, прилагая к нему силу. Самый простой вид деформации – это сжатие или растяжение. Коэффициент жесткости показывает именно то, какую силу необходимо приложить к телу, чтобы упруго деформировать его на единицу длины. Мы сейчас говорим об упругой деформации, когда тело принимает свою первоначальную форму после совершения воздействия на него. Для того чтобы провести этот наглядный эксперимент вам потребуются следующие вещи:

• калькулятор,
• ручка,
• тетрадь,
• пружина,
• линейка,
• груз.

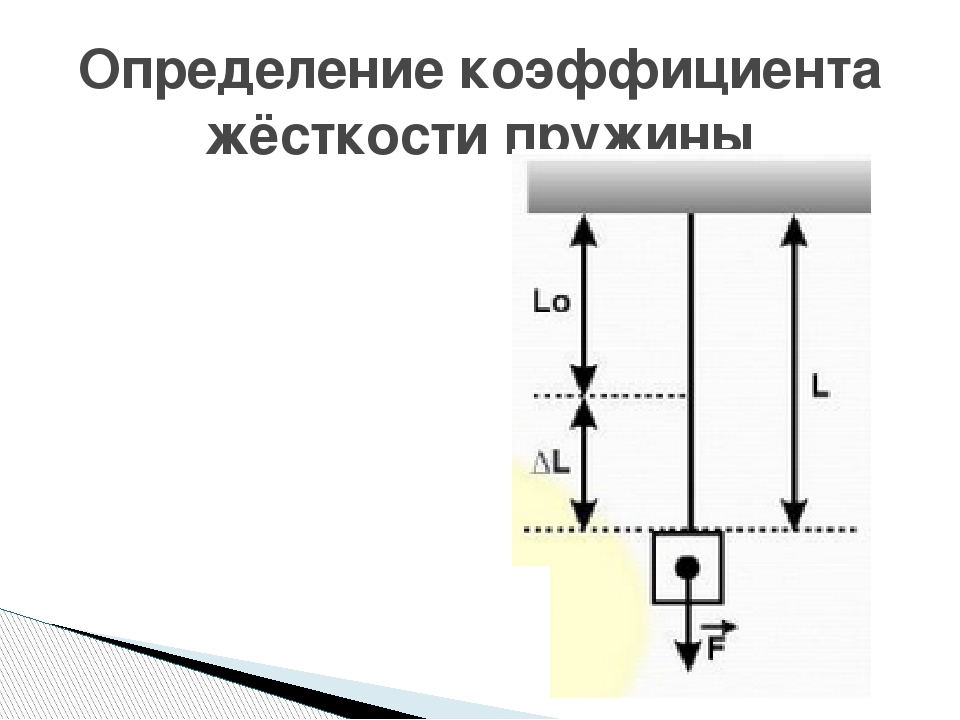
Итак, один конец пружины закрепите вертикально, а второй оставьте свободным. Измерьте длину пружины и запишите результат в тетрадь (это будет значение x1). Подвесьте к свободному концу пружины груз весом в сто граммов и опять измерьте длину пружины, запишите значение (x2). Рассчитайте абсолютное удлинение пружины (разница значений x1 и x2). При небольших сжатиях и растяжениях сила упругости пропорциональна деформации. Здесь уже применяем Закон Гука, согласно которому Fупр = |kx|, где k и является коэффициентом жесткости. Для того чтобы найти нужный нам коэффициент жесткости надо силу растяжения разделить на удлинение пружины. Силу растяжения находим следующим образом: Fупр = – N = -mg. Отсюда следует, что mg = kx. А значит, k = mg/x. Дальше все просто: подставьте известные вам значения в формулу и найдите, чему равна жёсткость пружины.

Если под воздействием внешних сил на твердое тело оно деформируется, то в нем происходят смещения частиц узлов кристаллической решетки. Этому сдвигу противостоят силы взаимодействия частиц. Так возникают силы упругости, которые приложены к телу, подвергшемуся деформации. Модуль силы упругости пропорционален деформации:

где — напряжение при упругой деформации, K — модуль упругости, который равен напряжению при относительной деформации, равной единице. где — относительная деформация, — абсолютная деформация, — первоначальное значение величины, которая характеризовала форму или размеры тела.

ОПРЕДЕЛЕНИЕ

Коэффициентом упругости
называют физическую величину, которая связывает в законе Гука удлинение, возникающее при деформации упругого тела и силу упругости. Величина равная называется коэффициентом упругости. Она показывает изменение размера тела под воздействием нагрузки при упругой деформации.

Коэффициент упругости зависит от материала тела, его размеров. Так при увеличении длины пружины и уменьшении ее толщины коэффициент упругости уменьшается.

Параллельное и последовательное соединение пружин

В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.

Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.

Последовательное соединение системы пружин

Последовательное соединение характерно наличием одной точки соединения пружин.

При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:

Коэффициент жесткости при последовательном соединении пружин 1/k = 1/k₁ + 1/k₂ + … + 1/k_i k — общая жесткость системы [Н/м] k1, k2, …, — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе

Параллельное соединение системы пружин

Последовательное соединение характерно наличием двух точек соединения пружин.

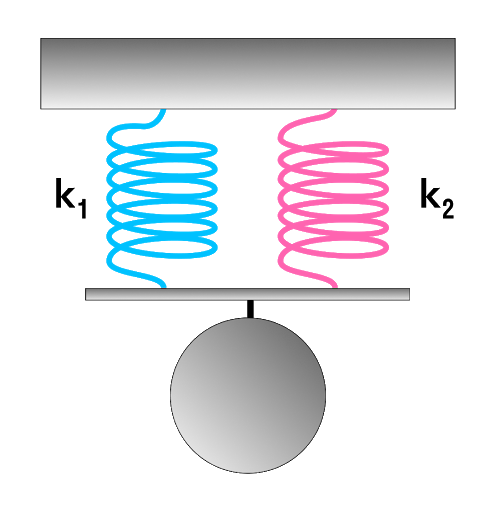
В случае когда пружины соединены параллельно величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:

Коэффициент жесткости при параллельном соединении пружин k = k₁ + k₂ + … + k_i k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе

Задачка

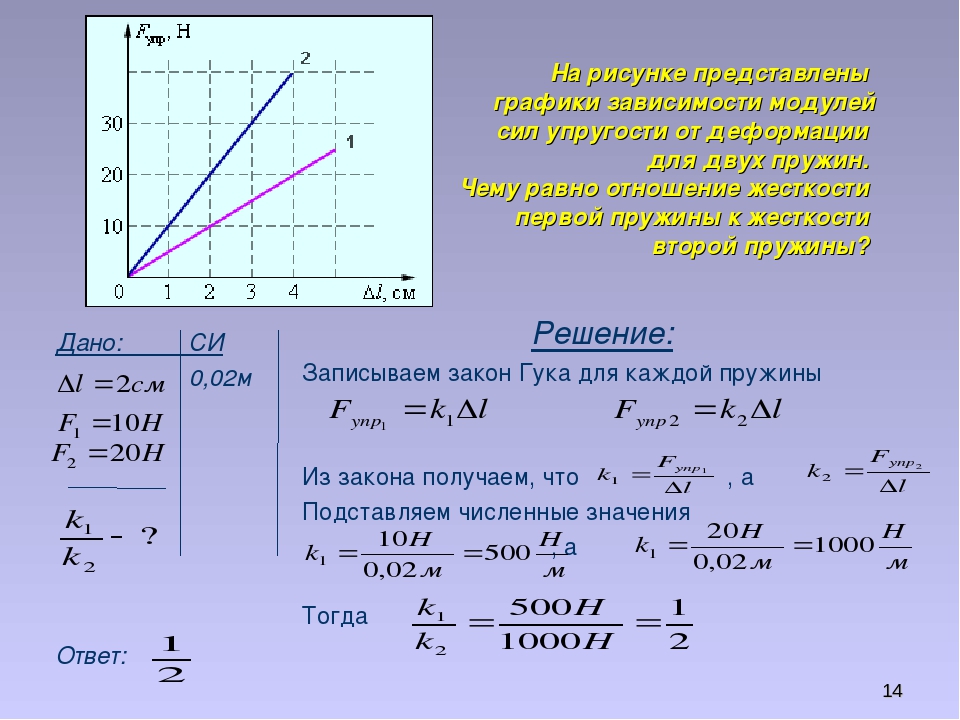
Какова жесткость системы из двух пружин, жесткости которых k₁ = 100 Н/м, k₂ = 200 Н/м, соединенных: а) параллельно; б) последовательно?

Решение:

а) Рассмотрим параллельное соединение пружин.

При параллельном соединении пружин общая жесткость

k = k₁ + k₂ = 100 + 200 = 300 Н/м

б) Рассмотрим последовательное соединение пружин.

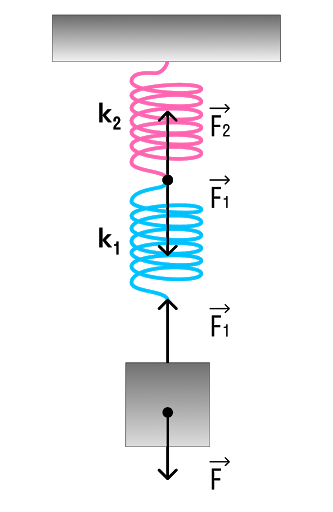
При последовательном соединении общая жесткость двух пружин

1/k = 1/100 + 1/200 = 0,01 + 0,005 = 0,015

k = 1000/15 = 200/3 ≃ 66,7 Н/м

Очень-очень важно!

Не забудь при расчете жесткости при последовательном соединении в конце перевернуть дробь

Класс «А» и «В» – существенны ли отличия

Для многих автолюбителей жесткость пружин по цветам равносильна жесткости по классам. Класс «А», независимо от цвета, более жесткий, нежели класс «В». На самом деле это не совсем верное утверждение. Класс «А» действительно больше подходит для автомобилей, которые часто эксплуатируются с высокой нагрузкой. Но разница здесь совсем невелика – порядка 25 кг. Несмотря на обязательное нанесение маркировки, до сих пор встречаются образцы, на которых она отсутствует. В таком случае, даже если цветовая маркировка элементов идентична, от их покупки и использования лучше отказаться.

Многими автомобилистами недооценивается значение качественных пружин, особенно при интенсивной эксплуатации автомобиля. Пружины не зря имеют маркировку по цветам – так гораздо проще сориентироваться начинающему водителю, который впервые занимается собственноручной заменой этого элемента. Приобретение изделий надлежащего качества, пусть и по более высокой цене, неизбежно окупится более мягкой ездой, меньшим износом автомобиля, а также меньшими нагрузками на самого водителя. Научно доказано, что высокие вибрационные нагрузки на человека приводят к быстрой утомляемости и снижению концентрации при движении.

Виды деформации

Деформация – это изменение формы, или размеров тела.

Есть несколько видов деформации:

• сдвиг;
• кручение;
• изгиб;
• сжатие/растяжение;

Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.

Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.

Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.

Рис. 1. пластиковая линейка, деформированная изгибом – а) и кручением – б)

В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.

Отличия пружин подвески и их маркировка

Основным идентификационным параметром любой пружины служит ее наружный диаметр. Производители не могут его самопроизвольно изменить, так как этот размер определяется конструктивными особенностями самого автомобиля. Все остальные параметры могут быть абсолютно различными. Так производители могут:

1. изменить диаметр прута, из которого она изготавливается и даже использовать прут, имеющий диаметр переменного значения;
2. изготавливать пружины одинаковой высоты, но различной жесткости;
3. изменить межвитковое расстояние и количество витков, сохраняя при этом жесткость.

Статья в тему: Как зарегистрироваться на экзамен в ГИБДД через госуслуги? Поэтому на заводах перед установкой проводят контроль статистической нагрузки. Проводится такая операция следующим образом: измеряют высоту пружины, сжав ее с определенным усилием. Так как для каждой конкретной модели автомобиля высота в сжатом состоянии регламентирована полем допуска, то детали, не попавшие в это поле, выбраковываются.

Пружины, попавшие в границы верхнего поля допуска относят к классу А (длинные), а в категорию В (короткие) попадают те, что имеют высоту в пределах нижнего поля допуска. Далее пружины одного класса маркируют краской, причем цвет маркировки зависит от модели автомобиля, на котором они должны быть установлены.

• Пружины класса А автомобилей ВАЗ маркируют по цвету желтой, белой, коричневой и оранжевой красками.
• Вид В также маркируют по цвету, но зеленой, голубой, синей и черной красками.

Маркировка по цвету наносится на внешнюю сторону витков в виде цветной полоски. Обилие цветов маркировочной краски объясняется тем, что с целью уменьшения влияния коррозии, они подвергают специальному покрытию (хлоркаучуковая эмаль или защитное эпоксидное покрытие), которое также бывает разного цвета (черное, серое, синее, белое, голубое) и определяет как модель автомобиля, так и назначение пружины (передняя или задняя). Причем на заводах, выпускающих различные модели ВАЗ и «Лада», передние элементы окрашены, как правило, в черный цвет. Исключение составляют только пружины с переменным межвитковым расстоянием (шагом) — они окрашиваются в голубой цвет.

Статья в тему: Самостоятельное приготовление электролита для АКБ

Расчет жесткости цилиндрической пружины

Довольно просто понять как работает плоская пружина. Если положить на край письменного стола линейку и прижать один ее конец рукой к поверхности, но второй можно упруго изгибать, запасая и высвобождая энергию. Очевидно, что в момент изгиба расстояния между молекулами материала в некоторых фрагментах линейки увеличиваются, в некоторых уменьшаются. Электромагнитные связи, действующие между молекулами, стремятся вернуть вещество к прежнему геометрическому состоянию.

Несколько сложнее дело обстоит с цилиндрической пружиной. В ней энергия запасается не благодаря деформации изгиба, а за счет скручивания проволоки, из которой пружина навита, относительно продольной оси этой проволоки.

Представим сильно увеличенное сечение проволоки, из которой навита цилиндрическая пружина, выполненное перпендикулярной ее оси плоскостью. При таком рассмотрении можно абстрагироваться от спиральной формы и мысленно разбить весь объем проволоки на множество соприкасающихся торцевыми поверхностями «цилиндров», диаметр которых равен диаметру проволоки, а высота стремится к нулю. Между соприкасающимися торцами действуют молекулярные силы, препятствующие деформации.

При растяжении или сжатии пружины угол наклона между витками изменяется. Соседние «цилиндры» при этом вращаются друг относительно друга в противоположных направлениях вокруг общей оси. В каждом таком сечении запасается энергия. Отсюда следует, что чем из более длинного куска проволоки навита пружина (здесь играют роль диаметр и высота цилиндра, а также шаг витка), тем большее количество энергии она способна запасти. Увеличение диаметра проволоки также повышает ее энергоемкость. В целом формула, учитывающая основные факторы жесткости пружины, выглядит так:

• $R$ — радиус цилиндра пружины,
• $n$ — количество витков проволоки радиуса $r$,
• $G$ — коэффициент, зависящий от материала.

Рассчитать коэффициент жесткости пружины, выполненной из стальной проволоки с $G = 8 cdot 10^$ Па и диаметром 1 мм. Радиус пружины 20 мм, количество витков — 25.

Подставим в формулу числовые значения, попутно переведя их в единицы системы СИ:

Ответ: $100 frac$

Так и не нашли ответ на свой вопрос?

Просто напиши с чем тебе нужна помощь

Источники и примечания

1. ↑Упругая деформация (рус.) . Архивировано из первоисточника 30 июня 2012.
2. ↑Dieter Meschede, Christian Gerthsen. Physik. — Springer, 2004. — P. 181..
3. ↑Bruno Assmann. Technische Mechanik: Kinematik und Kinetik. — Oldenbourg, 2004. — P. 11..
4. ↑Динамика, Сила упругости (рус.) . Архивировано из первоисточника 30 июня 2012.
5. ↑Механические свойства тел (рус.) . Архивировано из первоисточника 30 июня 2012.

Wikimedia Foundation . 2010 .

Смотреть что такое «Коэффициент упругости» в других словарях:

коэффициент упругости — tampros koeficientas statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, atvirkščiai proporcingas tampros moduliui. atitikmenys: angl. elasticity coefficient vok. Elastizitätskoeffizient, m rus. коэффициент упругости, m pranc.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

коэффициент упругости — tamprumo koeficientas statusas T sritis fizika atitikmenys: angl. elasticity coefficient vok. Elastizitätskoeffizient, m rus. коэффициент упругости, m pranc. coefficient d’élasticité, m … Fizikos terminų žodynas

КОЭФФИЦИЕНТ УПРУГОСТИ ПЛАСТА — β* σчитывающий упругое расширение жидкости, заключающейся в п., и уменьшение объема пор вследствие упругости пласта и характеризует упругий запас пластовой системы. К. у. п. определяют по формуле: βп = mβж + βп, где m… … Геологическая энциклопедия

Коэффициент упругости ар­матуры — – коэффициент, характеризующий упругопластическое состояние растянутой арматуры. Рубрика термина: Виды… … Энциклопедия терминов, определений и пояснений строительных материалов

Коэффициент упругости бе­тона — – коэффициент, характеризующий упругопластическое состояние сжатого бетона. Рубрика термина: Свойства бетона… … Энциклопедия терминов, определений и пояснений строительных материалов

КОЭФФИЦИЕНТ — КОЭФФИЦИЕНТ, число, на которое умножается некоторая неизвестная величина в алгебраическом выражении. В выражении 1 + 5х + 2х2 числа 5 и 2 являются коэффициентами х и х2 соответственно. В физике коэффициент это число, характеризующее определенное… … Научно-технический энциклопедический словарь

коэффициент — а, м. coefficient <, н. лат. coefficiens, ntis. 1. Мат. Множитель (числовой или буквенный) в алгебраическом выражении. Сл. 18. Надлежит же неоставить учинять делать примечании юношам при умножении алгебраическом возышение степеней. Как члены… … Исторический словарь галлицизмов русского языка

Коэффициент прочности — отношение фактического модуля упругости (прогиба) дорожной конструкции в данный момент времени к требуемому общему модулю упругости (прогибу), если дорожная одежда рассчитана по Инструкции title= Инструкция по проектированию дорожных одежд… … Словарь-справочник терминов нормативно-технической документации

Коэффициент запаса прочности — – отношение фактического модуля упругости дорожной одежды к требуемому модулю упругости, определенному по интенсивности и составу движения на период оценки фактического модуля упругости. Рубрика термина: Асфальт Рубрики… … Энциклопедия терминов, определений и пояснений строительных материалов

Закон Гука

Пружину можно сжимать, растягивать, изгибать или скручивать. В каждом из этих случаев будут возникать силы упругости, стремящиеся вернуть форму и размеры пружины в начальное состояние. Для понимания основных закономерностей будем рассматривать только линейные сжатия и растяжения (вдоль оси х). Для вычисления сил при деформациях изгибов и скручивании требуется применение более сложного математического аппарата.

Рис. 1. Деформации растяжения и сжатия пружины.

Если начальная длина, ненапряженной пружины, равна L, то для малых деформаций выполняется закон Гука, открытый экспериментально:

$ F_уп = − k * Δх $ (1),

где, в формуле силы упругости пружины:

F_уп — сила упругости пружины, Н;

k — коэффициент жесткости пружины, Н/м;

Δх —величина деформации (дельта икс), м.

Величина малых деформаций должна быть намного меньше начальной длины пружины:

$ Δх 0 — растяжение, и Δх

• Сила трения скольжения
• Сила тяжести
• Сила упругости
• Механическое движение
• Равнодействующая сила
• Неравномерное движение
• Взаимодействие тел
• Сила трения покоя
• Единица измерения массы
• Сила трения покоя
• Сила трения качения
• Причины возникновения силы трения
• Ускорение силы тяжести
• Сила упругости пружины
• Равномерное и неравномерное движение

показать все

По многочисленным просьбам теперь можно: сохранять все свои результаты, получать баллы и участвовать в общем рейтинге.

1. 1. Юлия Казакова 275
2. 2. Миша Дегтярев 261
3. 3. Алина Сайбель 140
4. 4. Екатерина Онегина 103
5. 5. Алина 98
6. 6. Марк Абрамов 90
7. 7. Алю Миний 87
8. 8. Дмитрий Аравин 75
9. 9. Ибрагим Мургустов 73
10. 10. Надежда Лавренова 72

1. 1. Мария Николаевна 12,965
2. 2. Лариса Самодурова 12,285
3. 3. Liza 11,735
4. 4. TorkMen 10,966
5. 5. Кристина Волосочева 10,910
6. 6. Ekaterina 10,791
7. 7. Лиса 10,720
8. 8. Юлия Бронникова 10,580
9. 9. Влад Лубенков 10,540
10. 10. Вячеслав 10,530

Самые активные участники недели:

• 1. Виктория Нойманн — подарочная карта книжного магазина на 500 рублей.
• 2. Bulat Sadykov — подарочная карта книжного магазина на 500 рублей.
• 3. Дарья Волкова — подарочная карта книжного магазина на 500 рублей.

Три счастливчика, которые прошли хотя бы 1 тест:

• 1. Наталья Старостина — подарочная карта книжного магазина на 500 рублей.
• 2. Николай З — подарочная карта книжного магазина на 500 рублей.
• 3. Давид Мельников — подарочная карта книжного магазина на 500 рублей.

Карты электронные(код), они будут отправлены в ближайшие дни сообщением Вконтакте или электронным письмом.

Формула определения жесткости

Изучаемая современными школьниками формула, как найти коэффициент жесткости пружины, представляет собой соотношение силы и величины, показывающей изменение длины пружины в зависимости от величины данного воздействия (или

Читать также: Устройство автомобильного гидравлического домкрата

равной ему по модулю силы упругости). Выглядит эта формула так: F = –kx. Из этой формулы коэффициент жесткости упругого элемента равен отношению силы упругости к изменению его длины. В международной системе единиц физических величин СИ он измеряется в ньютонах на метр (Н/м).

Другой вариант записи формулы: коэффициент Юнга

Деформация растяжения/сжатия в физике также может описываться несколько видоизмененным законом Гука. Формула включает значения относительной деформации (отношения изменения длины к ее начальному значению) и напряжения (отношения силы к площади поперечного сечения детали). Относительная деформация и напряжение по этой формуле пропорциональны, а коэффициент пропорциональности – величина, обратная модулю Юнга.

Модуль Юнга интересен тем, что определяется исключительно свойствами материала, и никак не зависит ни от формы детали, ни от ее размеров.

К примеру, модуль Юнга для ста

ли примерно равен единице с одиннадцатью нулями (единица измерения – Н/кв. м).

Смысл понятия коэффициент жесткости

Коэффициент жесткости – коэффициент пропорциональности из закона Гука. Еще он с полным правом называется коэффициентом упругости.

Фактически он показывает величину силы, которая должна быть приложена к упругому элементу, чтобы изменить его длину на единицу (в используемой системе измерений).

Значение этого параметра зависит от нескольких факторов, которыми характеризуется пружина:

• Материала, используемого при ее изготовлении.
• Формы и конструктивных особенностей.
• Геометрических размеров.

По этому показателю можно сд

елать вывод, насколько изделие устойчиво к воздействию нагрузок, то есть каким будет его сопротивление при приложении внешнего воздействия.

Особенности расчета пружин

Показывающая, как найти жесткость пружины, формула, наверное, одна из наиболее используемых современными конструкторами. Ведь применение эти упругие детали находят практически везде, то есть требуется просчитывать их поведение и выбирать те из них, которые будут идеально справляться с возложенными обязанностями.

Закон Гука весьма упрощенно показывает зависимость деформации упругой детали от прилагаемого усилия, инженерами используются более точные формулы расчета коэффициента жесткости, учитывающие все особенности происходящего процесса.

• Цилиндрическую витую пружину современная инженерия рассматривает как спираль из проволоки с круглым сечением, а ее деформация под воздействием существующих в системе сил представляется совокупностью элементарных сдвигов.
• При деформации изгиба в качестве деформации рассматривается прогиб стержня, расположенного концами на опорах.

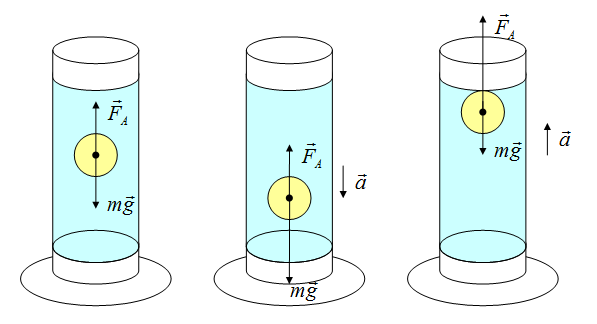
Сила Архимеда

Сила возникает в результате взаимодействия тела с жидкость (газом), при его погружении в жидкость (или газ). Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:

В воздухе силой Архимеда пренебрегаем.

Если сила Архимеда равна силе тяжести, тело плавает. Если сила Архимеда больше, то оно поднимается на поверхность жидкости, если меньше – тонет.

Существуют силы электрического происхождения. Возникают при наличии электрического заряда. Эти силы, такие как Сила Кулона, сила Ампера, сила Лоренца.

I закон Ньютона

Существуют такие системы отсчета, которые называются инерциальными, относительно которых тела сохраняют свою скорость неизменной, если на них не действуют другие тела или действие других сил скомпенсированно.

II закон Ньютона

Ускорение тела прямопропорционально равнодействующей сил, приложенных к телу, и обратно пропорционально его массе:

III закон Ньютона

Силы, с которыми два тела действуют друг на друга, равны по модулю и противоположны по направлению.

Локальная система отсчёта

— это система отсчёта, которая может считаться инерциальной, но лишь в бесконечно малой окрестности какой-то одной точки пространства-времени, или лишь вдоль какой-то одной незамкнутой мировой линии.

Преобразования Галилея. Принцип относительности в классической механике.

Преобразования Галилея. Рассмотрим две системы отсчета движущиеся друг относительно друга и с постоянной скоростью v.Одну из этих систем обозначим буквой K. Будем считать неподвижной. Тогда вторая система Kбудет двигаться прямолинейно и равномерно. Выберем координатные оси x,y,z системы K и x’,y’,z’ системы K’ так что оси x и x’ совпадали, а оси y и y’ , z и z’, были параллельны друг другу. Найдем связь между координатами x,y,z некоторой точки P в системе K и координатами x’,y’,z’ той же точки в системе K’. Если начать отсчёт времени с того момента, когда начало координат системы, совпадали, то x=x’+v, кроме того, очевидно, что y=y’, z=z’. Добавим к этим соотношениям принятое в классической механике предположение, что время в обеих системах течёт одинаковым образом, то есть t=t’. Получим совокупность четырёх уравнений : x=x’+vt;y=y’;z=z’;t=t’, названных преобразованиями Галилея.Механический принцип относительности.Положение о том, что все механические явления в различных инерциальных системах отсчёта протекают одинаковым образом, вследствие чего никакими механическими опытами невозможно установить, покоится ли система или движется равномерно и прямолинейно носит названия принцип относительности Галилея.Нарушение классического закона сложения скоростей.Исходя из общего принципа относительности (никаким физическим опытом нельзя отличить одну инерциальною систему от другой), сформулированным Альбертом Эйнштейном, Лоуренс изменил преобразования Галилиея и получил : x’=(x-vt)/(1-v 2 /c 2 ); y’=y; z’=z; t’=(t-vx/c 2 )/(1-v 2 /c 2 ). Эти преобразования называются преобразованиями Лоуренса.

Пружины можно назвать одной из наиболее распространенных деталей, которые являются частью простых и сложных механизмов. При ее изготовлении применяется специальная проволока, накручиваемая по определенной траектории. Выделяют довольно большое количество различных параметров, характеризующих это изделие. Наиболее важным можно назвать коэффициент жесткости. Он определяет основные свойства детали, может рассчитываться и применяться в других расчетах. Рассмотрим особенности подобного параметра подробнее.

Репетитор-онлайн — подготовка к ЦТ

Пример 16. При последовательном соединении трех пружин, коэффициенты жесткости которых относятся как 1 : 2 : 3, сила 12 Н вызвала растяжение системы на 4,0 см. Рассчитать коэффициенты жесткости указанных пружин.

Решение. Величина силы упругости, действующей на пружину, определяется формулой

F_упр = k_общ∆x,

где k_общ — коэффициент жесткости составной пружины; ∆x — указанное в условии задачи растяжение пружины.

Величина силы упругости, с другой стороны, совпадает с величиной приложенной силы:

F_упр = F.

Значение данной силы и величина растяжения пружины под действием этой силы позволяют рассчитать коэффициент жесткости составной пружины:

kобщ=FΔx=124,0⋅10−2=300 Н/м.

Для определения коэффициентов жесткости каждой пружины запишем их коэффициенты жесткости в следующем виде:

для первой пружины

k₁ = k;

для второй пружины

k₂ = 2k;

для третьей пружины

k₃ = 3k,

так как указанные коэффициенты по условию задачи соотносятся между собой как

k₁ : k₂ : k₃ = 1 : 2 : 3.

Для расчета величины k запишем формулу для коэффициента жесткости пружины, состоящей из трех последовательно соединенных пружин, и подставим в нее выражения k₁, k₂, k₃:

1kобщ=1k1+1k2+1k3=1k+12k+13k=116k, или kобщ=6k11.

Найденное ранее значение k_общ = 300 Н/м позволяет рассчитать k = 550 Н/м.

Тогда коэффициенты жесткости каждой из пружин имеют значения:

для первой пружины

k₁ = k = 550 Н/м;

для второй пружины

k₂ = 2k = 1100 Н/м;

для третьей пружины

k₃ = 3k = 1650 Н/м.