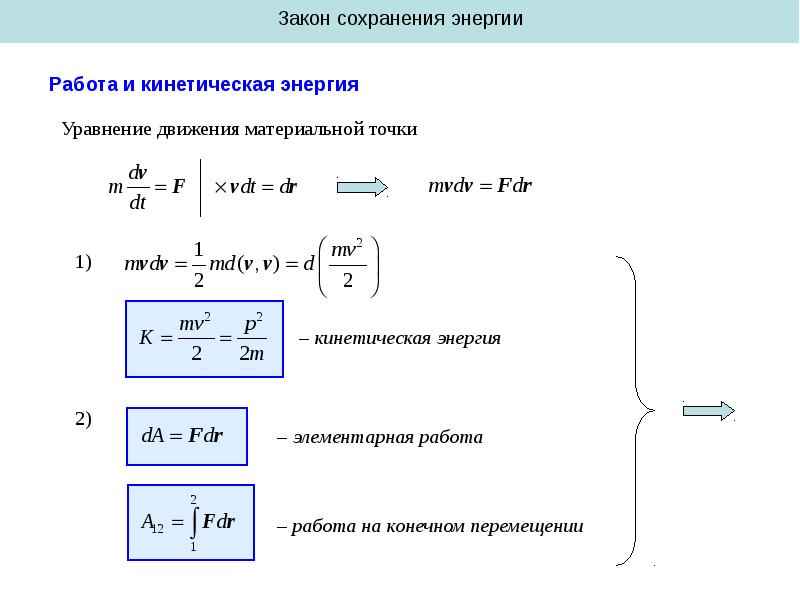
Основные понятия и законы кинематики
Часть механики, в которой изучают движение, не рассматривая причины, вызывающие тот или иной характер движения, называют кинематикой .Механическим движением называют изменение положения тела относительно других телСистемой отсчёта называют тело отсчёта, связанную с ним систему координат и часы.Телом отсчёта называют тело, относительно которого рассматривают положение других тел.Материальной точкой называют тело, размерами которого в данной задаче можно пренебречь.Траекторией называют мысленную линию, которую при своём движении описывает материальная точка. По форме траектории движение делится на: а)прямолинейное — траектория представляет собой отрезок прямой; б)криволинейное — траектория представляет собой отрезок кривой.Путь — это длина траектории, которую описывает материальная точка за данный промежуток времени. Это скалярная величина.Перемещение — это вектор, соединяющий начальное положение материальной точки с её конечным положением (см. рис.).
Очень важно понимать, чем путь отличается от перемещения. Самое главной отличие в том, что перемещение — это вектор с началом в точке отправления и с концом в точке назначения (при этом абсолютно неважно, каким маршрутом это перемещение совершалось)
А путь — это, наборот, скалярная величина, отражающая длину пройденной траектории.
Равномерным прямолинейным движением
называют движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещенияСкоростью равномерного прямолинейного движения называют отношение перемещения ко времени, за которое это перемещение произошло:
Для неравномерного движения пользуются понятием средней скорости.
Часто вводят среднюю скорость как скалярную величину. Это скорость такого равномерного движения, при котором тело проходит тот же путь за то же время, что и при неравномерном движении:
Мгновенной скоростью
называют скорость тела в данной точке траектории или в данный момент времени.Равноускоренное прямолинейное движение — это прямолинейное движение, при котором мгновенная скорость за любые равные промежутки времени изменяется на одну и ту же величинуУскорением называют отношение изменения мгновенной скорости тела ко времени, за которое это изменение произошло:
Зависимость координаты тела от времени в равномерном прямолинейном движении имеет вид: x = x0 + Vxt
, где x0 — начальная координата тела, Vx — скорость движения.Свободным падением называют равноускоренное движение с постоянным ускорениемg = 9,8 м/с2 , не зависящим от массы падающего тела. Оно происходит только под действием силы тяжести.
Скорость при свободном падении рассчитывается по формуле: Перемещение по вертикали рассчитывается по формуле:
Одним из видов движения материальной точки является движение по окружности. При таком движении скорость тела направлена по касательной, проведённой к окружности в той точке, где находится тело (линейная скорость). Описывать положение тела на окружности можно с помощью радиуса, проведённого из центра окружности к телу. Перемещение тела при движении по окружности описывается поворотом радиуса окружности, соединяющего центр окружности с телом. Отношение угла поворота радиуса к промежутку времени, в течение которого этот поворот произошёл, характеризует быстроту перемещения тела по окружности и носит название угловой скорости ω
Угловая скорость связана с линейной скоростью соотношением где r — радиус окружности. Время, за которое тело описывает полный оборот, называется периодом обращения.
Величина, обратная периоду — частота обращения —ν Поскольку при равномерном движении по окружности модуль скорости не меняется, но меняется направление скорости, при таком движении существует ускорение. Его называют центростремительным ускорением
, оно направлено по радиусу к центру окружности:
Физика
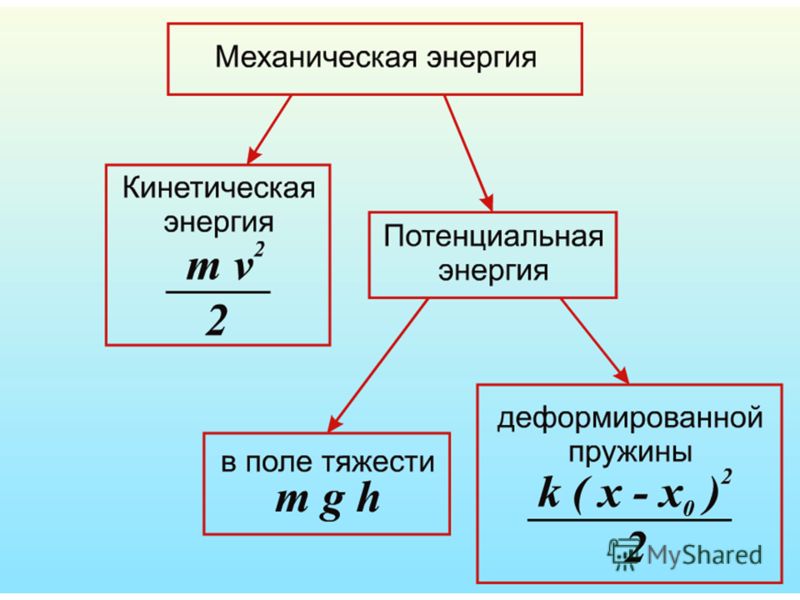
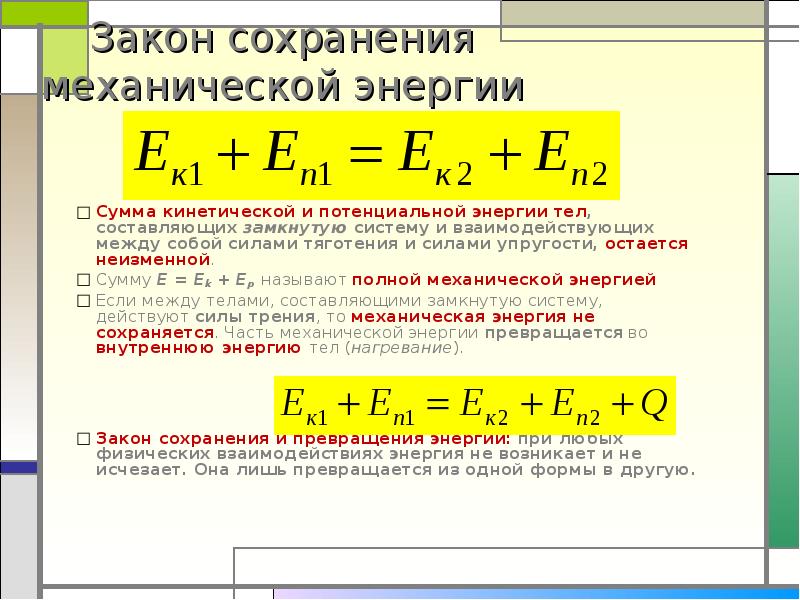
3.4. Механическая энергия
3.4.2. Потенциальная энергия
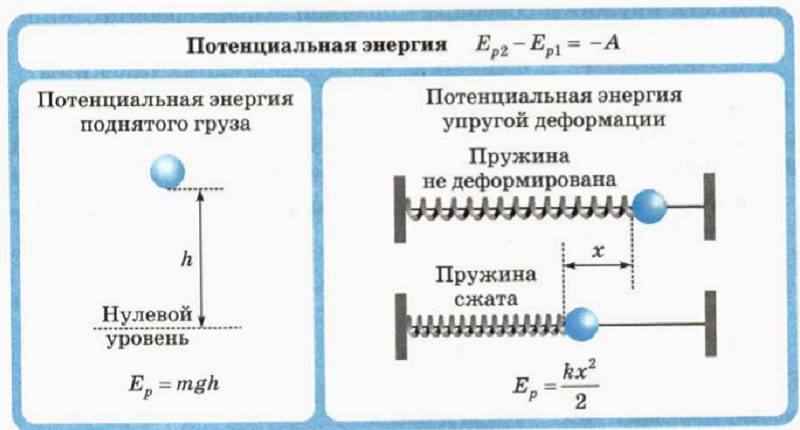
Потенциальная энергия — это механическая энергия системы тел, определяемая их (или частей одного тела) взаимным расположением.
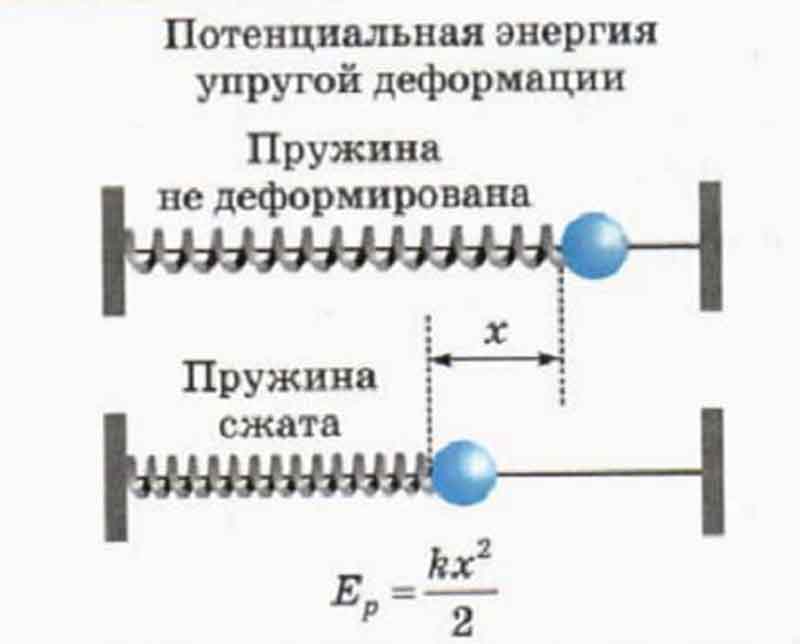
Потенциальная энергия деформированной пружины
Деформированная пружина (сжатая или растянутая) (рис. 3.7) обладает потенциальной энергией, которая определяется формулой
W p = k ( Δ l ) 2 2 ,
где k — коэффициент жесткости (упругости) пружины; ∆l — величина абсолютной деформации пружины (удлинения или сжатия).
Рис. 3.7
Потенциальная энергия недеформированной пружины равна нулю.
Следует отметить, что потенциальная энергия деформированной пружины всегда является положительной величиной.
В Международной системе единиц потенциальная энергия деформированной пружины измеряется в джоулях (1 Дж).
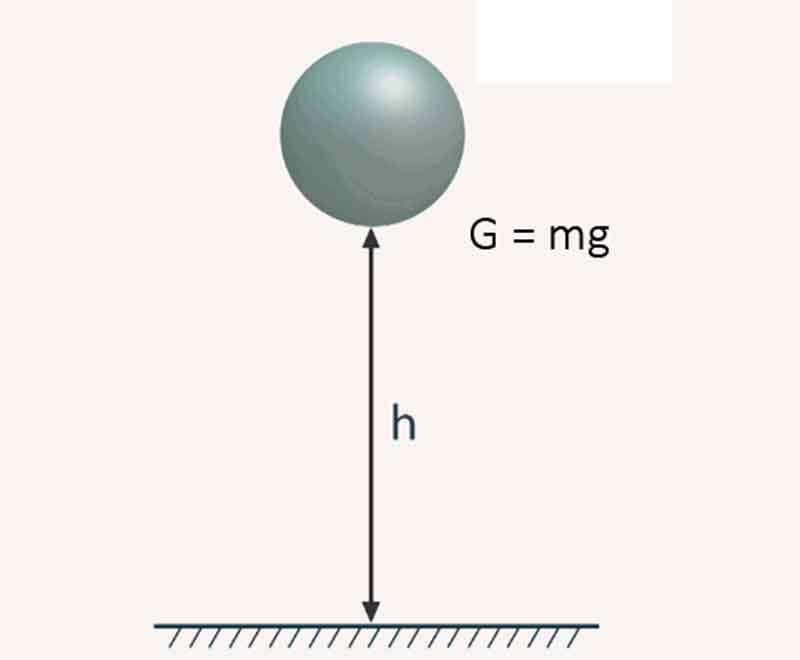
Потенциальная энергия взаимодействия тела и Земли
Тело, расположенное на расстоянии h над поверхностью Земли (или под ее поверхностью), обладает потенциальной энергией, которая определяется формулой
Wp = mgh + C,
где m — масса тела; g — модуль ускорения свободного падения.
Выбор константы C является условным и зависит от конкретной задачи; часто указанную константу выбирают таким образом, чтобы на поверхности планеты потенциальная энергия взаимодействия тела и планеты обращалась в ноль.
Следует отметить, что потенциальная энергия взаимодействия тела и Земли может быть как положительной, так и отрицательной величиной.
В Международной системе единиц потенциальная энергия тела, поднятого на некоторую высоту относительно поверхности Земли, измеряется в джоулях (1 Дж).
Пример 26. Две пружины с одинаковыми коэффициентами жесткости по 1,0 кН/м соединили последовательно. Составную пружину растянули на 10 см. Во сколько раз увеличится потенциальная энергия деформации, если эти же пружины соединить параллельно, а величину деформации системы оставить прежней? Рассчитать потенциальную энергию пружин при последовательном и параллельном соединении, считая деформацию составной пружины одинаковой и равной 10 см.
Решение. Потенциальная энергия составной пружины определяется формулой
W p = k общ ( Δ l ) 2 2 ,
где kобщ — общий коэффициент жесткости составной пружины; ∆l — величина деформации пружины.
Коэффициент жесткости составной пружины определяется по-разному:
для N одинаковых пружин, соединенных последовательно,
k общ 1 = k 0 N ;
для N одинаковых пружин, соединенных параллельно,
kобщ2 = Nk0,
где k0 — коэффициент жесткости одной пружины; N = 2 — количество соединенных пружин.
Потенциальная энергия составной пружины вычисляется по формулам:
для N одинаковых пружин, соединенных последовательно,
W p 1 = k общ 1 ( Δ l ) 2 2 = k 0 ( Δ l ) 2 2 N ;
для N одинаковых пружин, соединенных параллельно,
W p 2 = k общ 2 ( Δ l ) 2 2 = N k 0 ( Δ l ) 2 2 .
Отношение потенциальных энергий
W p 1 W p 2 = k 0 ( Δ l ) 2 2 N 2 N k 0 ( Δ l ) 2 = 1 N 2
определяется только количеством пружин и не зависит от деформации составной пружины.
Рассчитаем потенциальную энергию составной пружины, состоящей из двух одинаковых пружин,
соединенных последовательно:
W p 1 = k 0 ( Δ l ) 2 2 N = 1,0 ⋅ 10 3 ( 10 ⋅ 10 − 2 ) 2 2 ⋅ 2 = 2,5 Дж;
соединенных параллельно:
W p 2 = N k 0 ( Δ l ) 2 2 = 2 ⋅ 1,0 ⋅ 10 3 ( 10 ⋅ 10 − 2 ) 2 2 = 10 Дж.
Отношение указанных потенциальных энергий равно
W p 1 W p 2 = 1 N 2 = 1 2 2 = 4 .
Следовательно, при одинаковой деформации потенциальная энергия пружины, составленной из двух одинаковых параллельно соединенных пружин, в 4 раза больше потенциальной энергии пружины, составленной из двух одинаковых последовательно соединенных пружин.
Пример 27. Какой энергией обладает тело массой 500 г на вершине горы относительно дна озера, находящегося у подножия горы? Высота горы составляет 1,50 км, а глубина озера 250 м.
Решение. Потенциальная энергия тела, поднятого на некоторую высоту, определяется формулой
Wp = mgh,
где m — масса тела; g — модуль ускорения свободного падения; h — высота, на которую поднято тело над определенным уровнем, характеризуемым нулевым значением потенциальной энергии.
Выберем нулевой уровень потенциальной энергии (Wp = 0) на дне озера так, как показано на рисунке.
Тогда высота, на которую поднято тело над указанным уровнем, является суммой:
h = h2 + h2,
где h2 = 1,50 км — высота горы; h2 = 250 м — глубина озера.
Потенциальная энергия тела относительно дна озера определяется выражением
Wp = mg(h2 + h2).
Расчет дает значение:
W p = 500 ⋅ 10 − 3 ⋅ 10 ⋅ ( 1,50 + 0,25 ) ⋅ 10 3 = 8,75 ⋅ 10 3 Дж = 8,75 кДж.
Максимальная кинетическая энергия груза на пружине
Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.
Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению:
В этом соотношении ω – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:
Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими .
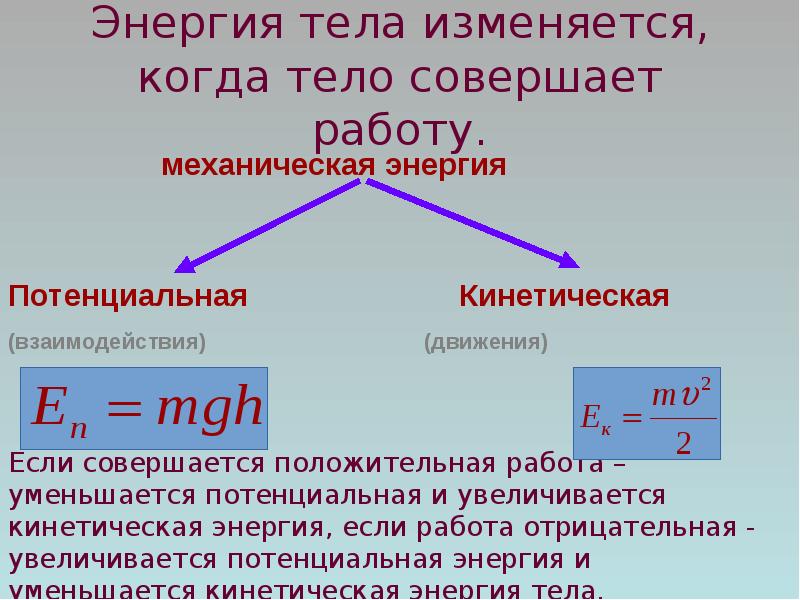
При свободных механических колебаниях кинетическая и потенциальная энергии изменяются периодически. При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на горизонтально расположенной пружине потенциальная энергия – это энергия упругих деформаций пружины.
Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д.
Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот.
Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной.
Для груза на пружине:
Запуск колебательного движения тела осуществляется с помощью кнопки Старт . Остановить процесс в любой момент времени позволяет кнопка Стоп .
Графически показано соотношение между потенциальной и кинетической энергиями при колебаниях в любой момент времени
Обратите внимание, что в отсутствие затухания полная энергия колебательной системы остается неизменной, потенциальная энергия достигает максимума при максимальном отклонении тела от положения равновесия, а кинетическая энергия принимает максимальное значение при прохождении тела через положение равновесия
Задание 7. Верхний конец пружины идеального пружинного маятника неподвижно закреплён, как показано на рисунке. Масса груза маятника равна m, жёсткость пружины равна k. Груз оттянули вниз на расстояние x от положения равновесия и отпустили с начальной скоростью, равной нулю. Формулы А и Б позволяют рассчитать значения физических величин, характеризующих колебания маятника.
Установите соответствие между формулами и физическими величинами, значение которых можно рассчитать по этим формулам.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
1) амплитуда колебаний скорости
2) циклическая частота колебаний
3) максимальная кинетическая энергия груза
4) период колебаний
А) Имеем пружинный маятник массой m и жесткостью пружины k, тогда период свободных колебаний этого маятника определяется по формуле
Б) Для пружинного маятника известны формулы кинетической энергии
Пружинный маятник, состоящий из груза и лёгкой пружины, совершает колебания. В момент, когда груз находится в крайнем положении, его немного подталкивают вдоль оси пружины в направлении от положения
равновесия. Как в результате этого изменяются максимальная кинетическая энергия груза маятника и частота его колебаний?
Для каждой величины определите соответствующий характер изменения:
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Максимальная кинетическая энергия груза маятника | Частота колебаний маятника |
Груз подтолкнули от положения равновесия, откуда следует, что амплитуда колебаний груза увеличится. При этом увеличится также и максимальная потенциальная энергия пружины. По закону сохранения энергии, это приведет к увеличению максимальной кинетической энергии груза маятника.
Период и частота пружинного маятника зависят только от массы груза и жесткости пружины. Таким образом, при увеличении амплитуды колебаний груза, частота колебаний маятника не изменится.
Контрольные вопросы
Что называется деформацией? Какие деформации называются упругими? Приведите примеры упругих деформаций.
Какова физическая сущность упругих сил?
Сформулируйте закон Гука? Когда он справедлив?
Дайте объяснение качественной диаграмме напряжений. Что такое предел пропорциональности, упругости и прочности?
Что такое упругий гистерезис и упругое последействие?
Каков физический смысл модуля Юнга и модуля сдвига?
Что такое упругое последействие?
Выведите выражения для деформаций при всестороннем растяжении.
Что называется коэффициентом Пуассона?
Определите энергию деформированного тела.
Что называется плотностью упругой энергии? Получите формулы этой энергии при растяжении и сдвиге.
А. mv²/2 Б.mv В.mgh Г. kx²/2 2. Каково наименование единицы кинетической энергии, выраженное через основные единицы Международной системы? А.1кг·м Б.1 кг·м/с В.1кг·м²/с Г.1кг·м²/с² 3. Чему равна кинетическая энергия тела массой 3 кг, движущегося со скоростью 4 м/с?
Читать также: Почему стиральная машинка сильно вибрирует при отжиме
А. 6 Дж. Б. 12 Дж. В.24Дж. Г.48Дж.
4. Как изменится потенциальная энергия упруго деформированного тела при увеличении его деформации в три раза?
À. Не изменится. Б. Увеличится в 3 раза. . Увеличится в 9 раз. Г. Увеличится в 27 раз.
Два автомобиля с одинаковыми массами m движутся со скоростями v и 3v относительно Земли в одном направлении. Чему равна кинетическая энергия второго автомобиля в системе отсчета, связанной с первым автомобилем?
А.mv² Б.2mv² В.3mv² Г.4mv² 6.Каково наименование единицы работы, выраженное через основные единицы Международной системы? А.1кг Б.1кг·м/с В.1кг·м/с² Г.1кг·м²/с² 7.По какой формуле следует рассчитывать работу силы F, если между направлением силы и перемещения S угол a ? А.(F/S)·cosα Б.F·S·sinα В.F·S·cosα Г.(F·S)·sinα
9. Тело массой 1 кг силой 30 Н поднимается на высоту 5 м. Чему равна работа этой силы?
А .0 Дж. Б. 50 Дж. В. 100 Дж. Г. 150 Дж.
Кинетическая энергия тела в момент бросания равна 200 Дж. Определите, до какой высоты от поверхности земли может подняться тело, если его масса равна 500 г.
Башенный кран поднимает бетонную плиту массой 2 т на высоту 15 м. Чему равна работа силы тяжести, действующей на плиту?
Вычисление работы силы упругости
Груз совершил известное перемещение, величину силы упругости мы также знаем, векторы перемещения и силы упругости параллельны. Казалось бы, все ясно – нужно умножить величину силы на величину перемещения и получить значение работы. Однако здесь не все так просто – разберемся почему.
О чем нам говорит формула, которая выражает величину силы упругости? О том, что сила упругости – величина не постоянная, она меняется по мере перемещения груза. И действительно, величина этой силы, как мы видим из формулы, зависит от координаты центра груза. Формула же для работы силы, которую мы применяли раньше, справедлива лишь в том случае, если сила не меняет свою величину по мере движения. Как же тогда быть? Один из вариантов выхода из данной ситуации мог бы состоять в том, что мы применим такой же метод, который применялся нами ранее в разделе кинематика при расчете перемещения тела, движущегося равноускоренно.
Можно всю траекторию движения груза разбить на очень маленькие участки (участки, в пределах которых силу упругости можно считать практически постоянной). Далее в пределах каждого такого участка мы можем рассчитать работу силы упругости ввиду ее практического постоянства. Затем работа на всей области движения груза будет складываться из всех этих маленьких работ на этих участках. Таким образом, мы сможем посчитать работу силы упругости на всей траектории движения груза. На рис. 4 приведены детали такого расчета.
Рис. 4. Зависимость силы упругости от координаты движения
Видно, что если отложить на графике зависимость модуля силы упругости от модуля координаты груза, затем проделать описанное выше разбиение на маленькие участки, то величина работы на каждом маленьком участке численно равна площади фигуры, ограниченной графиком: осью абсцисс и двумя перпендикулярами к этой оси (см. рис. 5).
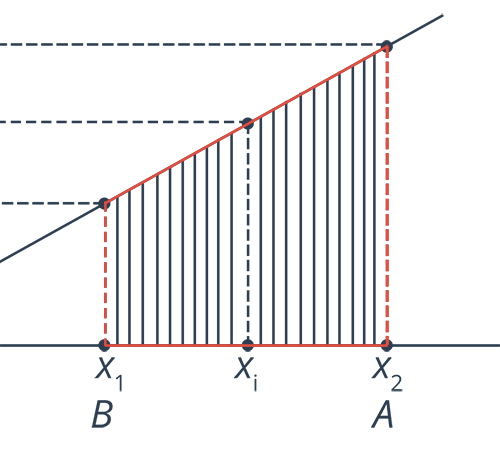
Рис. 5. Площадь фигуры
Если просуммировать значение работы на каждом участке (площадь маленьких фигур), то получим площадь большой фигуры, показанной на рис. 6.
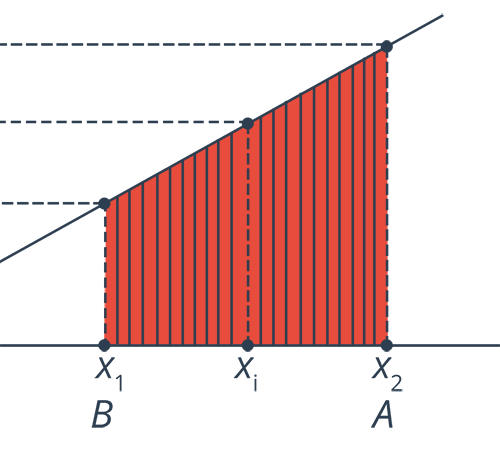
Рис. 6. Площадь большой фигуры
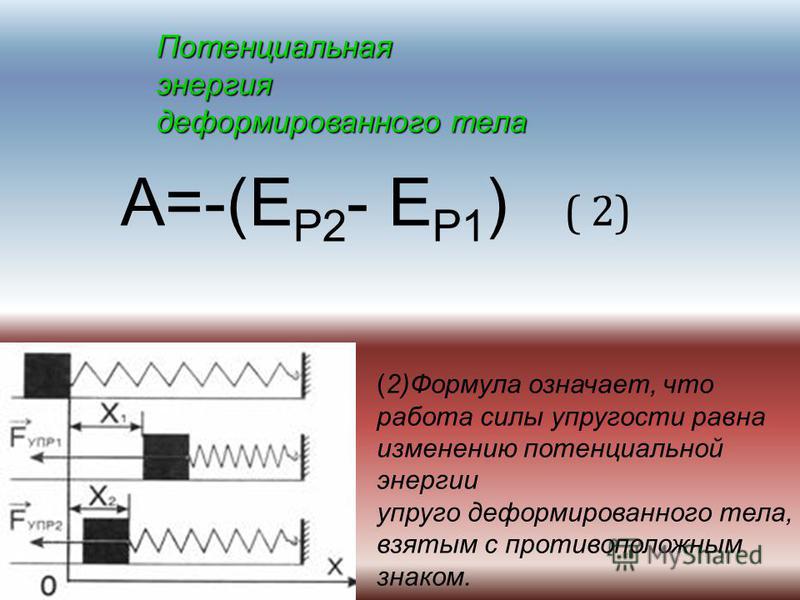
Поскольку данная фигура является прямоугольной трапецией, то мы можем воспользоваться формулой для расчета площади такой фигуры – это полусумма оснований, умноженная на высоту. В результате преобразований получим такую формулу – работа равна разности между величиной:
К этому результату можно прийти и несколько иным способом. Для вычисления работы силы упругости в этом способе необходимо просто взять среднее значение силы упругости и умножить его на перемещение тела. Это утверждение можно записать как:
,
где среднее значение силы упругости, которое равно полусумме начального и конечного ее значений. Если данное выражение подставить в формулу для работы, то при помощи простых алгебраических преобразований мы получим то же самое выражение, что получали ранее:
Как видно из этой формулы, работа зависит лишь от начальной и конечной координаты центра груза, и еще одно замечание: как видно из последней формулы, работа силы упругости никоим образом не зависит от массы груза. Это обусловлено тем, что и сама сила упругости не зависит от этой массы.
Теперь внимательнее посмотрим на последнюю формулу – если вынести -1 за скобки, то получим, что работа есть взятая со знаком минус разность между значениями некоторой величины, равной половине произведения жесткости пружины на квадрат ее удлинения в конечный и начальный моменты времени.
Вспомним, как мы поступили при расчете работы силы тяжести на прошлом уроке. В тот раз мы столкнулись с новой для нас физической величиной, разность между значениями которой в конечной и начальной моменты времени равнялась взятой со знаком « — » работе силы тяжести. Это величина, равная произведению массы тела на ускорение свободного падения и высоту, на которую было поднято тело над некоторым уровнем, мы назвали потенциальной энергией тела, поднятого над землей.
Максимальная кинетическая энергия груза
Для простого пружинного маятника полную энергию груза в любой момент времени можно выразить как
- $E_p$ — потенциальная энергия,
- $E_k$ — кинетическая энергия,
- $m$ — масса,
- $v$ — моментальная скорость,
- $k$ — коэффициент упругости,
- $x$ — приращение длины пружины в данный момент.
Задай вопрос специалистам и получи ответ уже через 15 минут!
Максимальную кинетическую энергию можно вычислить как
где $v_ $ — максимальная скорость груза. Однако измерить ее на практике сложно. Проще, опираясь на постоянство суммы кинетической и потенциальной энергий, определить максимальную потенциальную (когда кинетическая равна нулю). Поскольку справедливо и обратное, можно записать:
где $x_ $ — максимальное приращение растяжения пружины. Его легко измерить, а коэффициент упругости посмотреть в справочнике.
Компактный груз, массой 0,5 кг прикреплен к движущейся горизонтально пружине. Ее коэффициент упругости равен 2000 $frac $. Каково было начальное приращение длины пружины, если его максимальная скорость во время колебаний составляет 1 $frac $?
Из условий задачи можно найти максимальную кинетическую энергию груза:
Выразив максимальную потенциальную энергию через приращение длины пружины, составим равенство:
Ответ: $approx 1,6 мм$.
Так и не нашли ответ на свой вопрос?
Просто напиши с чем тебе нужна помощь
Груз математического маятника массой 10 г совершает гармонические колебания. При этом скорость v груза изменяется с течением времени t по закону v = 2sin ( 0,5πt )
Чему равна максимальная кинетическая энергия груза при таких колебаниях?
помогите пожалуйста — вот я знаю Е кин = mv^2/2 но от куда я должна взять значения. что взять из этой формулы? ( v = 2sin ( 0,5πt )) 2 — это скорость, которую можно подставить в Е? 0,5 это w , с этим что то сделать?
оу. не я получила 0,02. Тааак. а в каких это единицах? это равно 2м дж?
При свободных механических колебаниях кинетическая и потенциальная энергии изменяются периодически. При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на горизонтально расположенной пружине потенциальная энергия – это энергия упругих деформаций пружины. Для математического маятника – это энергия в поле тяготения Земли.
Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д.
Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот .
Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной.
Задачи на тему «Законы сохранения в механике»
Задача №1. Закон сохранения энергии
Условие
На какую высоту поднимется тело, подброшенное вертикально вверх, с начальной скоростью 10 м/с? При решении задачи не учитывается сопротивление воздуха.
Решение
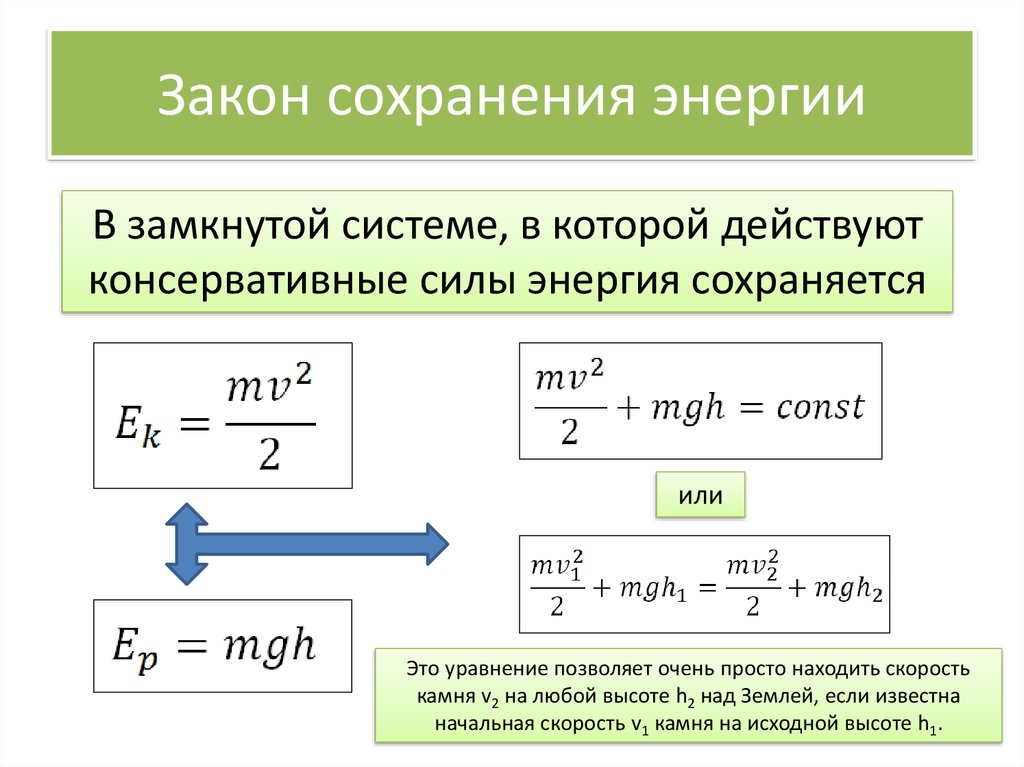
По закону сохранения энергии, начальная кинетическая энергия брошенного тела будет равна его потенциальной энергии в наивысшей точке подъема.
Ответ: 5,1м
Задача №2. Закон сохранения импульса
Условие
Определите скорости двух шаров массами m1 и m2 после центрального абсолютно упругого удара. Скорости шаров до удара v1 и v2 соответственно
Решение
В задаче применяется закон сохранения импульса. Запишем его в векторном виде и в проекции на горизонтальную ось в соответствии с рисунком:
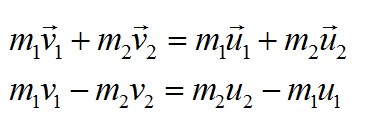
Теперь запишем закон сохранения энергии:
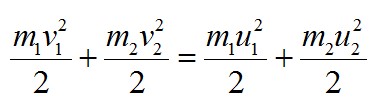
Преобразуем полученные выражения:
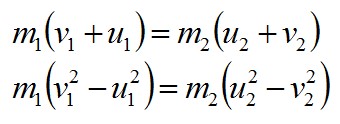
Воспользуемся формулами сокращенного умножения, разделим правые и левые части системы друг на друга и получим:
Подставим выраженное значение u2 в первое уравнение для закона сохранения импульса и получим:
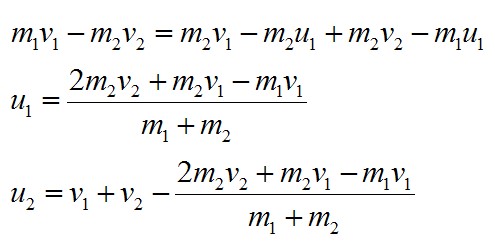
Ответ: см. решение
Задача №3. Закон сохранения энергии
Условие
Спусковую пружину игрушечного пистолета сжали на 5 см, при вылете шарик массой 20 г приобрел скорость 2 м/с. Необходимо рассчитать, какова жесткость пружины
Решение
Потенциальная энергия деформированной пружины переходит в кинетическую энергию шарика
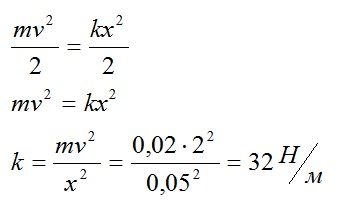
Ответ: 32 Н/м
Задача №4. Закон сохранения момента импульса
Условие
Платформа, имеющая форму сплошного однородного диска, может вращаться по инерции вокруг неподвижной вертикальной оси. На краю платформы стоит человек, масса которого в 3 раза меньше массы платформы. Определите, как и во сколько раз изменится угловая скорость вращения платформы, если человек перейдёт ближе к центру на расстояние, равное половине радиуса платформы.
Решение
Так как в системе человек–платформа сумма моментов сил тяжести и реакции опоры равна нулю, для решения задачи можно применить закон сохранения момента импульса
Запишем моменты инерции системы в начальном и конечном состояниях, затем подставим результат во второе выражение:
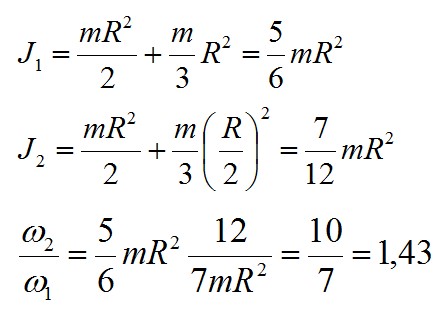
Ответ: угловая скорость увеличится в 1,43 раза.
Задача №5. Закон сохранения энергии
Условие
При растяжении пружины на 20 см она приобрела потенциальную энергию упругодеформированного тела 20 Дж. Какова жесткость пружины?
Решение
Потенциальная энергия пружины вычисляется по формуле
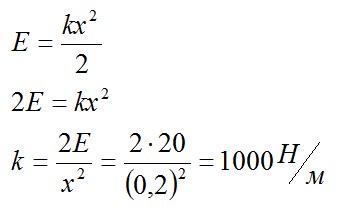
Ответ: 1000 Н/м
Кстати! Для наших читателей действует скидка 10% на любой вид работы
Закон сохранения энергии в тепловых процессах
Чтобы закон сохранения энергии для тепловых процессов был сформулирован, было сделано два важных шага. Сначала французский математик и физик Жан Батист Фурье установил один из основных законов теплопроводности. А потом Сади Карно определил, что тепловую энергию можно превратить в механическую.
Вот что сформулировал Фурье:
При переходе теплоты от более горячего тела к более холодному температуры тел постепенно выравниваются и становятся едиными для обоих тел — наступает состояние термодинамического равновесия. |
Таким образом, первым важным открытием было открытие того факта, что все протекающие без участия внешних сил тепловые процессы необратимы.
Дальше Карно установил, что тепловую энергию, которой обладает нагретое тело, непосредственно невозможно превратить в механическую энергию для производства работы. Это можно сделать, только если часть тепловой энергии тела с большей температурой передать другому телу с меньшей температурой и, следовательно, нагреть его до более высокой температуры.
Закон сохранения энергии в тепловых процессах При теплообмене двух или нескольких тел абсолютное количество теплоты, которое отдано более нагретым телом, равно количеству теплоты, которое получено менее нагретым телом. |
Математически его можно описать так:
Уравнение теплового баланса Q отд = Q пол Qотд — отданное системой количество теплоты Q пол — полученное системой количество теплоты |
Данное равенство называется уравнением теплового баланса. В реальных опытах обычно получается, что отданное более нагретым телом количество теплоты больше количества теплоты, полученного менее нагретым телом:
Это объясняется тем, что некоторое количество теплоты при теплообмене передаётся окружающему воздуху, а ещё часть — сосуду, в котором происходит теплообмен.
Задачка раз
Сколько граммов спирта нужно сжечь в спиртовке, чтобы нагреть на ней воду массой 580 г на 80 °С, если учесть, что на нагревание пошло 20% затраченной энергии.
Удельная теплота сгорания спирта 2,9·10^7Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг·°С).
Решение:
При нагревании тело получает количество теплоты
Q = cmΔt ,
где c — удельная теплоемкость вещества
При сгорании тела выделяется энергия
Qсгор = q*mсгор,
где q — удельная теплота сгорания топлива
По условию задачи нам известно, что на нагревание пошло 20% затраченной энергии.
То есть:
Q = 0,2 * Qсгор
cmΔt =0,2 * qmсгор
mсгор = cmΔt / 0,2 q
Ответ: масса сгоревшего топливаа равна 33,6 г.
Задачка два
Какое минимальное количество теплоты необходимо для превращения в воду 500 г льда, взятого при температуре −10 °С? Потерями энергии на нагревание окружающего воздуха пренебречь. Удельная теплоемкость льда равна 2100 Дж/кг*℃, удельная теплота плавления льда равна 3,3*10^5 Дж/кг.
Решение:
Для нагревания льда до температуры плавления необходимо:
Qнагрев = cmΔt
Qнагрев = 2100 * 0,5 * (10-0) = 10500 Дж
Для превращения льда в воду:
Qпл = λm
Qпл = 3,3 * 10^5 * 0,5 = 165000 Дж
Таким образом:
Q = Qнагрев + Qпл = 10500 + 165000 = 175500 Дж = 175,5 кДж
Ответ: чтобы превратить 0,5 кг льда в воду при заданных условиях необходимо 175,5 кДж тепла.
Основные понятия и законы динамики
Часть механики, изучающая причины, вызвавшие ускорение тел, называется динамикой
Первый закон Ньютона:
Cуществуют такие системы отсчёта, относительно которых тело сохраняет свою скорость постоянной или покоится, если на него не действуют другие тела или действие других тел скомпенсировано.
Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при уравновешенных внешних силах, действующих на него, называется инертностью. Явление сохранения скорости тела при уравновешенных внешних силах называют инерцией. Инерциальными системами отсчёта называют системы, в которых выполняется первый закон Ньютона.
Принцип относительности Галилея:во всех инерциальных системах отсчёта при одинаковых начальных условиях все механические явления протекают одинаково, т.е. подчиняются одинаковым законамМасса — это мера инертности телаСила — это количественная мера взаимодействия тел.
Второй закон Ньютона:Сила, действующая на тело, равна произведению массы тела на ускорение, сообщаемое этой силой:
$F{→} = m⋅a{→}$
Сложение сил заключается в нахождении равнодействующей нескольких сил, которая производит такое же действие, как и несколько одновременно действующих сил.
Третий закон Ньютона: Силы, с которыми два тела действуют друг на друга, расположены на одной прямой, равны по модулю и противоположны по направлению:
$F_1{→} = -F_2{→} $
III закон Ньютона подчёркивает, что действие тел друг на друга носит характер взаимодействия. Если тело A действует на тело B, то и тело B действует на тело
A (см. рис.).
Или короче, сила действия равна силе противодействия. Часто возникает вопрос: почему лошадь тянет сани, если эти тела взаимодействуют с равными силами? Это возможно только за счёт взаимодействия с третьим телом — Землёй. Сила, с которой копыта упираются в землю, должна быть больше, чем сила трения саней о землю. Иначе копыта будут проскальзывать, и лошадь не сдвинется с места.
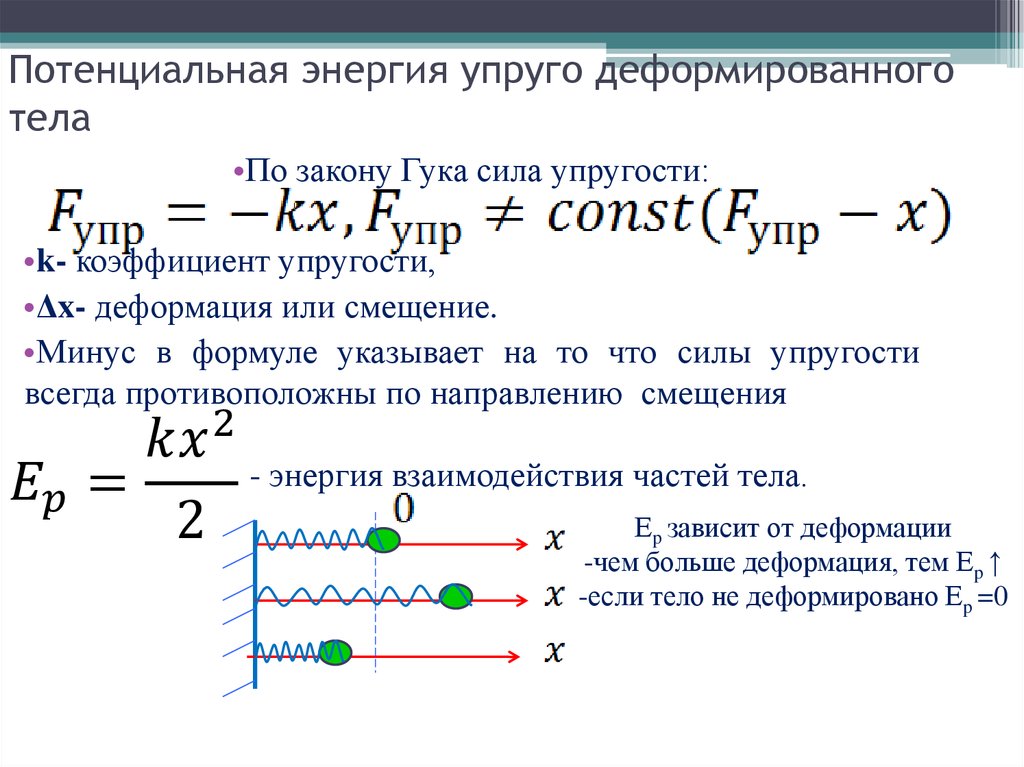
Если тело подвергнуть деформации, то возникают силы, препятствующие этой деформации. Такие силы называют силами упругости.
Закон Гука записывают в виде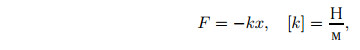
где k — жёсткость пружины, x — деформация тела. Знак «−» указывает, что сила и деформация направлены в разные стороны.
При движении тел друг относительно друга возникают силы, препятствующие движению. Эти силы называются силами трения. Различают трение покоя и трение скольжения. Сила трения скольжения подсчитывается по формуле
где N — сила реакции опоры, µ — коэффициент трения.
Эта сила не зависит от площади трущихся тел. Коэффициент трения зависит от материала, из которого сделаны тела, и качества обработки их поверхности.
Трение покоя возникает, если тела не перемещаются друг относительно друга. Сила трения покоя может меняться от нуля до некоторого максимального значенияГравитационными силами называют силы, с которыми любые два тела притягиваются друг к другу.
Закон всемирного тяготения:
Весом телаСила тяжести
НевесомостьюИскусственный спутник ЗемлиПервая космическая скорость
1.3. Основные понятия и законы статики и гидростатики
устойчивое, неустойчивое и безразличное.устойчивое равновесие.неустойчивое положениебезразличное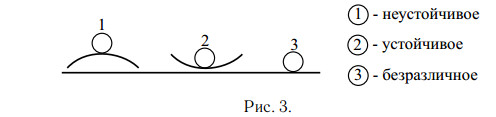
Плечом силыУсловие равновесия рычага:Давлениемзакон Паскаля:
Гидравлический пресс
A1 = A2.силой Архимедазакон Архимеда
жидкпогрУсловие плавания тела
1.4. Законы сохранения
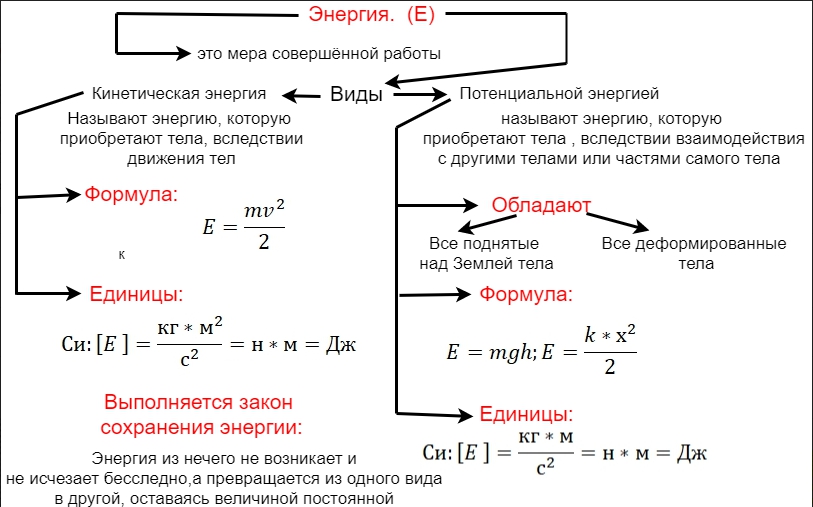
Импульсом тела
импульсом силы.закон сохранения импульсаМеханической работой
Мощность
энергией.кинетическую и потенциальную.кинетической энергией.
потенциальной энергией.
Энергия сжатой пружины:
механическую энергию.закон сохранения механической энергии
1.5. Механические колебания и волны
КолебаниямиГармоническими колебаниями
амплитудой колебанийПериодом TЧастотой периодических колебаний-1Математическим маятникомПериод колебаний математического маятника
Период колебаний груза на пружине
Распространение колебаний в упругих средах.поперечнойпродольнойДлиной волны
Звуковыми волнами
Сила упругости в пружинном маятнике
Следует учитывать тот момент, что до деформирования пружины она находится в положении равновесия. Приложенная сила может приводить к ее растягиванию и сжиманию. Сила упругости в пружинном маятнике рассчитывается в соответствии с тем, как воздействует закон сохранения энергии. Согласно принятым нормам возникающая упругость пропорциональна смещению тела. В этом случае кинетическая энергия рассчитывается по формуле: F=-kx. В данном случае применяется коэффициент жесткости пружины.
Выделяют довольно большое количество особенностей воздействия силы упругости в пружинном маятнике. Среди особенностей отметим:
- Максимальная сила упругости возникает на момент, когда тело находится на максимальном расстоянии от положения равновесия. При этом в подобном положении отмечается максимальное значение ускорение тела. Не следует забывать о том, что может проводится растягивание и сжатие пружины, оба варианта несколько отличается. При сжатии минимальная длина изделия ограничивается. Как правило, она имеет длину, равную диаметру витка умноженное на количество. Слишком большое усилие может стать причиной смещения витков, а также деформации проволоки. При растяжении есть момент удлинения, после которого происходит деформация. Сильное удлинение приводит к тому, что возникающей силы упругости недостаточно для возврата изделия в первоначальное состояние.
- При сближении тела к месту равновесия происходит существенное уменьшение длины пружины. За счет этого наблюдается постоянное снижение показателя ускорения. Все это происходит за счет воздействия усилия упругости, которая связано с типом применяемого материала при изготовлении пружины и ее особенностями. Длина уменьшается за счет того, что расстояние между витками снижается. Особенностью можно назвать равномерное распределение витков, лишь только в случае дефектов есть вероятность нарушения подобного правила.
- На момент достижения точки равновесия сила упругости снижается до нуля. Однако, скорость не снижается, так как тело движется по инерции. Точка равновесия характеризуется тем, что длина изделия в ней сохраняется на протяжении длительного периода при условии отсутствия внешнего деформирующего усилия. Точка равновесия определяется в случае построения схемы.
- После достижения точки равновесия возникающая упругость начинает снижать скорость перемещения тела. Она действует в противоположном направлении. При этом возникает усилие, которое направлено в обратную сторону.
- Дойдя крайней точки тело начинает двигаться в противоположную сторону. В зависимости от жесткости установленной пружины подобное действие будет повторятся неоднократно. Протяженность этого цикла зависит от самых различных моментов. Примером можно назвать массу тела, а также максимальное приложенное усилие для возникновения деформации. В некоторых случаях колебательные движения практически незаметны, но они все же возникают.
Приведенная выше информация указывает на то, что колебательные движения совершаются за счет воздействия упругости. Деформация происходит за счет приложенного усилия, которое может варьировать в достаточно большом диапазоне, все зависит от конкретного случая.
