Зубчатое колесо

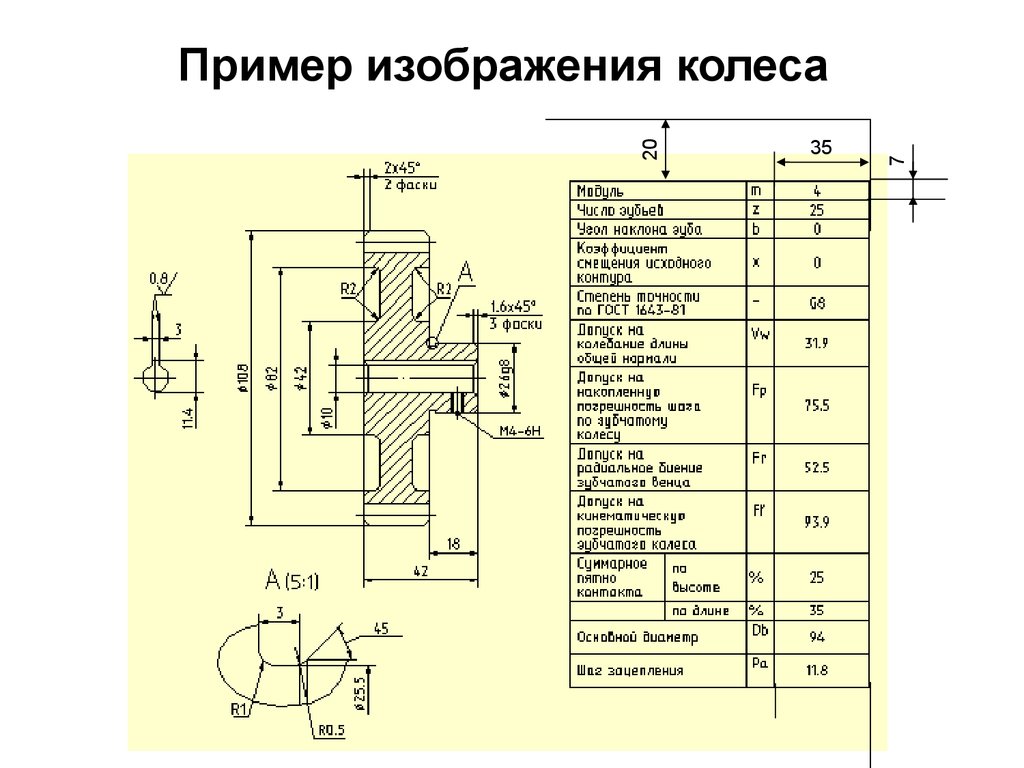
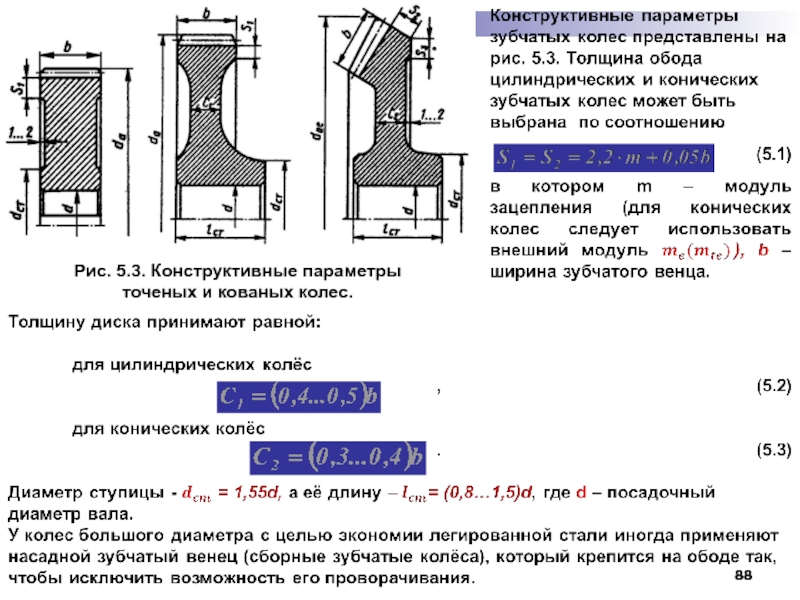
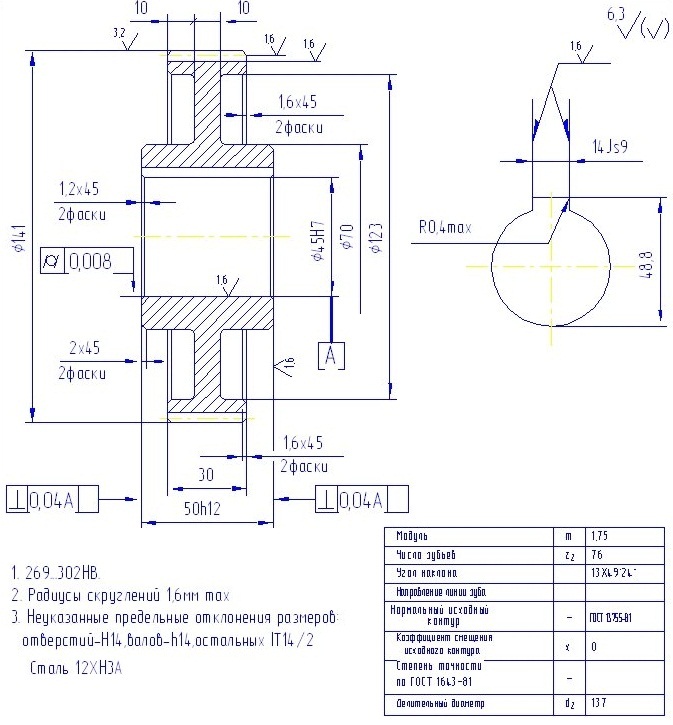
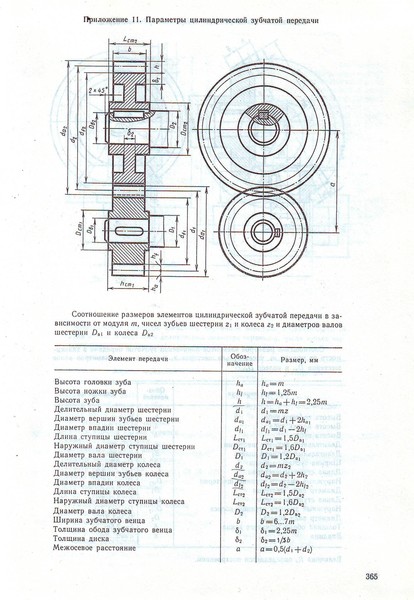
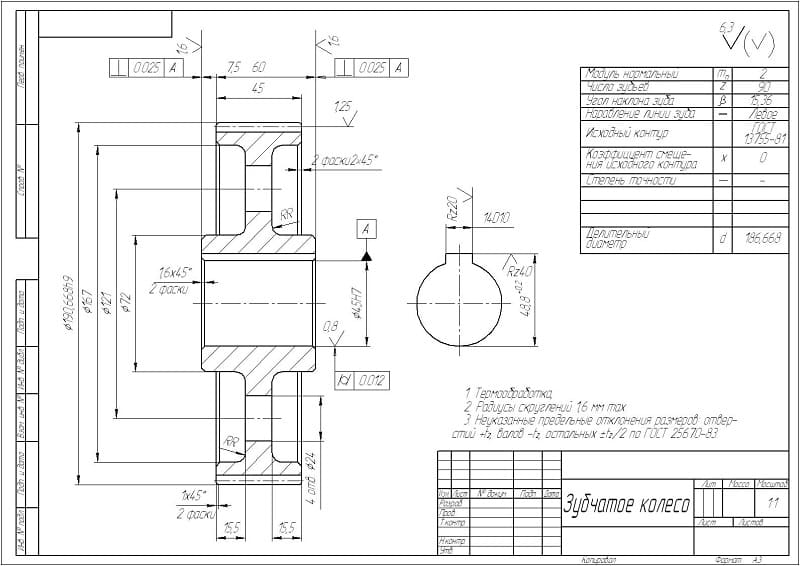
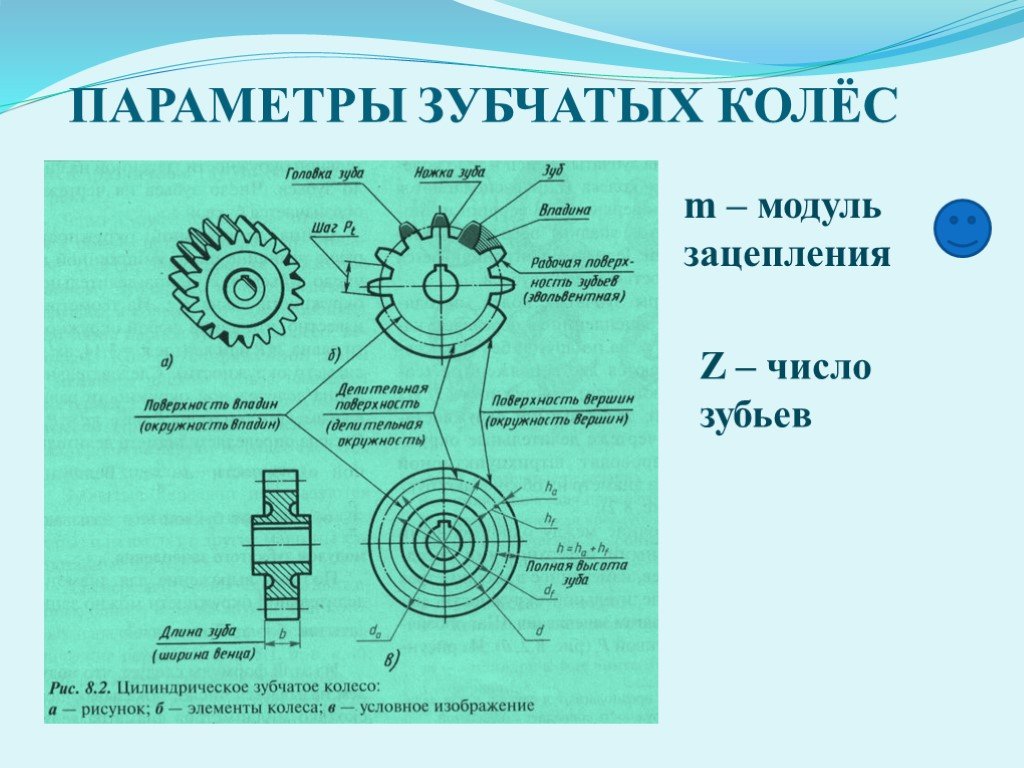
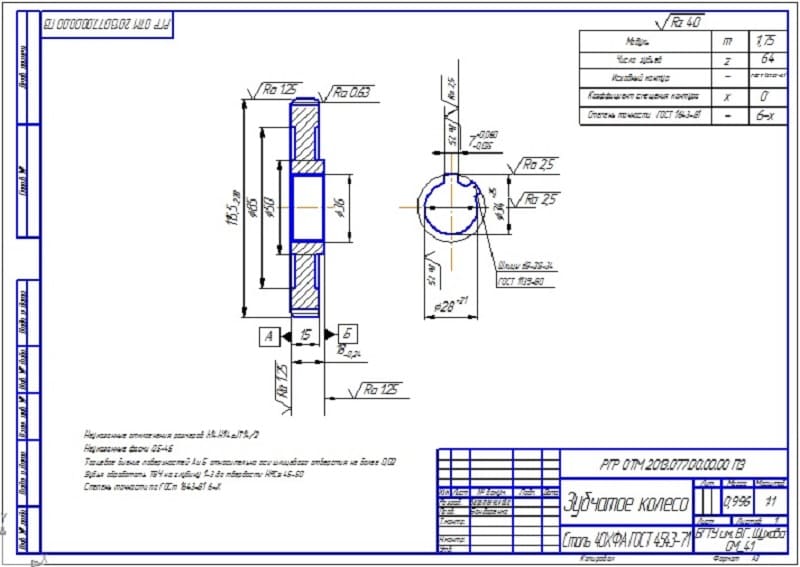
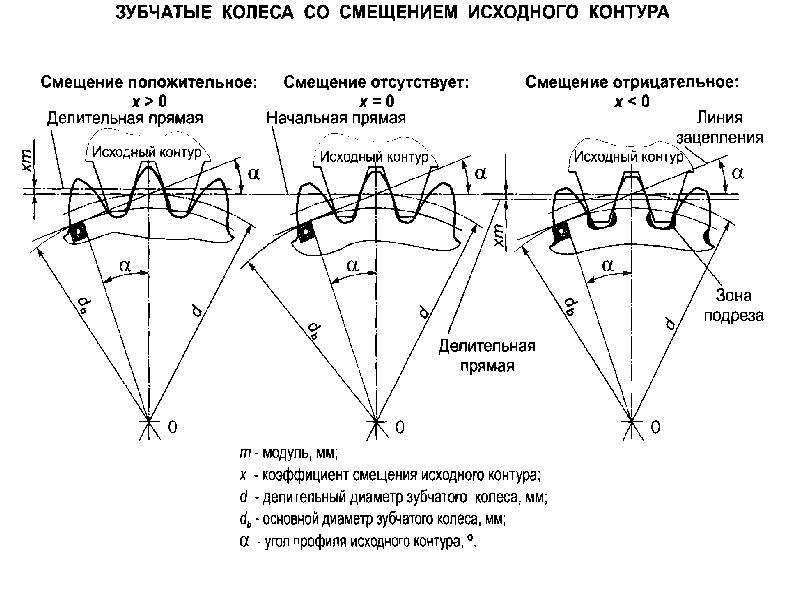
Чем отличается зубчатое колесо от шестерни

Еще один момент, на который следует обратить внимание. Конечно, в разговорной речи эти понятия идентичны, но с технической точки зрения шестерня отличается от зубчатого колеса

И различие в основном связано не с особенностями конструкции, а функцией, выполняемой в механизме.

Согласно перечню основных терминов, приведенных в ГОСТ 16530-83, шестерня — зубчатое колесо с меньшим числом зубьев для редукторов и большим числом для мультипликаторов. Если в механизм входят детали с одинаковым количеством зубьев, то шестерней считается ведущая деталь, а зубчатым колесом — ведомая. Отметим, что на практике применяется еще одна разновидность — вал-шестерня, которая представляет собой вал с нарезанными непосредственно на нем зубьями. Все перечисленные детали являются основными элементами механических зубчатых передач.

Исходные данные и замеры

На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.

Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.

Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.

Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.

Результаты расчетов

Для более крупных потребуются измерения и вычисления.

Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:

m=De/(z+2)

Последовательность действий следующая:

• измерить диаметр штангенциркулем;
• сосчитать зубцы;
• разделить диаметр на z+2;
• округлить результат до ближайшего целого числа.

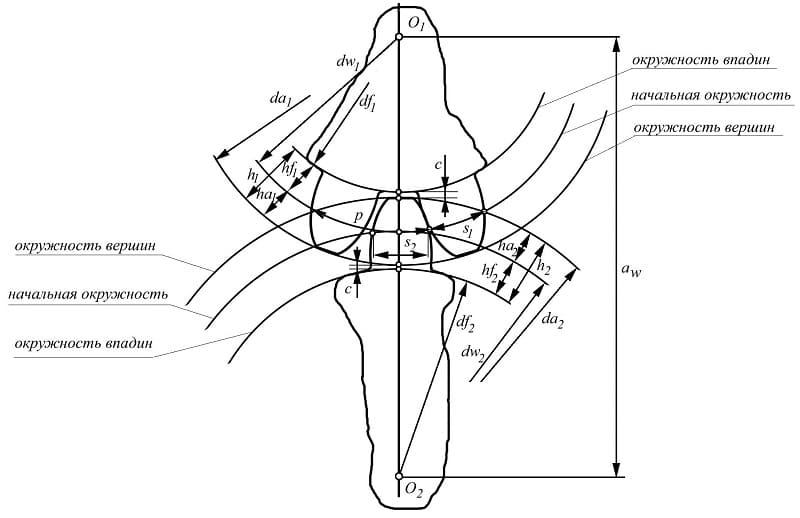
Зубец колеса и его параметры

Данный метод подходит как для прямозубых колес, так и для косозубых.

Достоинства и недостатки зубчатых передач

Прежде всего, среди достоинств зубчатой передачи можно выделить:

• высокую надежность с учетом расширенного диапазона нагрузок и скоростей;
• компактность, большой ресурс и высокий КПД;
• относительно небольшие нагрузки на валы и подшипники;
• постоянное передаточное число (отношение);
• простота изготовления и обслуживания;

Также выделяют и недостатки зубчатой передачи:

• повышенные требования к качеству изготовления и точности установки;
• при высокой скорости вращения возникает шум по причине возможных неточностей при изготовлении шага и профиля зубьев;
• повышенная жесткость не позволяет эффективно компенсировать динамические нагрузки, в результате чего возникает разрушение и пробуксовки, появляются дефекты;

Напоследок отметим, что во время обслуживания механизм нужно осматривать, производя проверку состояния зубчатых колес, шестерен и зубьев на предмет повреждений, трещин, сколов  и т.д.

Также проверяется само зацепление и его качество (часто используется краска, которая наносится на зубья). Нанесение краски позволяет изучить величину пятна контакта, а также расположение относительно высоты зуба. Для регулировки зацепления применяются прокладки, которые ставятся в подшипниковые узлы.

Форма зуба

Зацепления различаются по профилю и типу зубьев. По форме зуба различают эвольвентные, круговые и циклоидальные зацепления. Наиболее часто используемыми являются эвольвентные зацепления. Они имеют технологическое превосходство. Нарезка зубьев может производиться простым реечным инструментом. Эти зацепления характеризуются постоянным передаточным отношением, не зависящим от смещения межцентрового расстояния. Но при больших мощностях проявляются недостатки, связанные с небольшим пятном контакта в двух выпуклых поверхностях зубьев. Это может приводить к поверхностным разрушениям и выкрашиванию материала поверхностей.

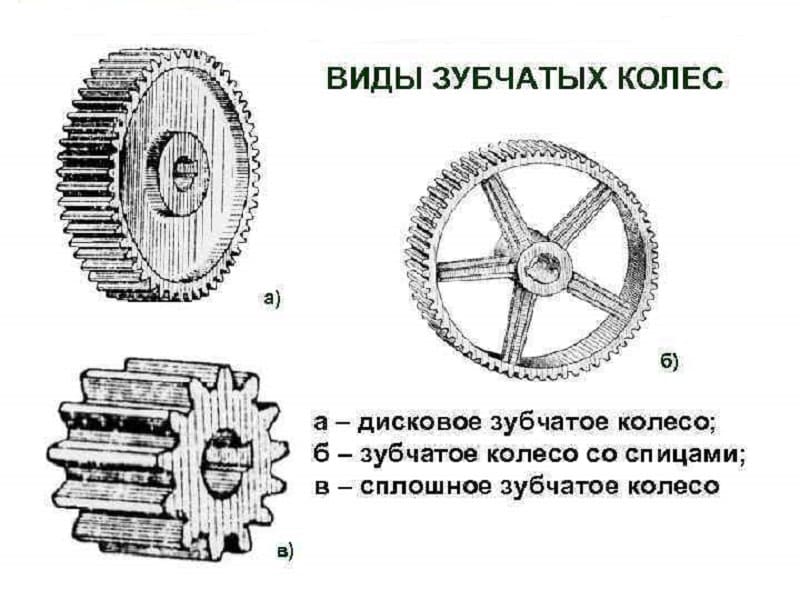
В круговых зацеплениях выпуклые зубья шестерни сцепляются с вогнутыми колесами и пятно контакта значительно увеличивается. Недостатком этих передач является то, что появляется трение в колёсных парах. Виды зубчатых колёс:

1. Прямозубые. Это наиболее часто используемый вид колёсных пар. Контактная линия у них параллельна оси вала. Прямозубые колёса сравнительно дешевы, но максимальный передаваемый момент у них меньше, чем у косозубых и шевронных колёс.
2. Косозубые. Рекомендуется применять при больших частотах вращения, они обеспечивают более плавный ход и уменьшение шума. Недостатком является повышенная нагрузка на подшипники из-за возникновения осевых усилий.
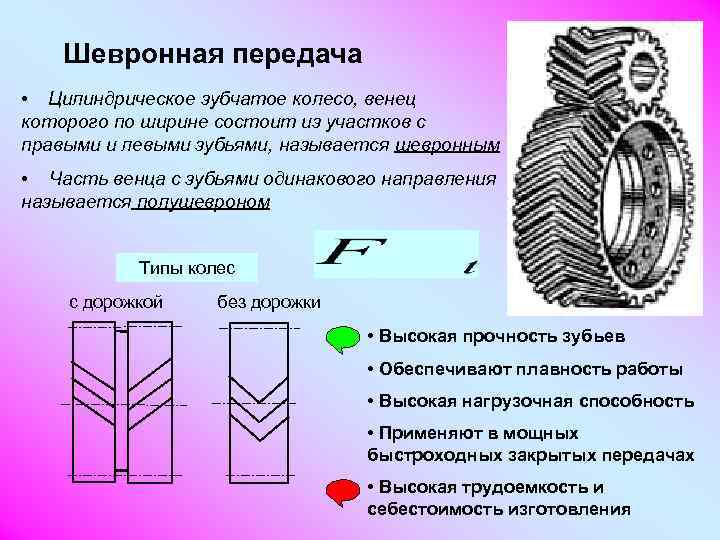
3. Шевронные. Обладают преимуществами косозубых колёсных пар и не нагружают подшипники осевыми силами, так как силы направлены в разные стороны.
4. Криволинейные. Применяются при больших передаточных отношениях. Менее шумные и лучше работают на изгиб.

Прямозубые колёсные пары имеют наибольшее распространение. Их легко проектировать, изготавливать и эксплуатировать.

Как рассчитать передаточное число

Шестерня и колесо имеют разное количество зубов с одинаковым модулем и пропорциональный размер диаметров. Передаточное число показывает, сколько оборотов совершит ведущая деталь, чтобы провернуть ведомую на полный круг. Зубчатые передачи имеют жесткое соединение. Передающееся количество оборотов в них не меняется. Это негативно сказывается на работе узла в условиях перегрузок и запыленности. Зубец не может проскользнуть, как ремень по шкиву и ломается.

Расчет без учета сопротивления

В расчете передаточного числа шестерен используют количество зубьев на каждой детали или их радиусы.

Где u12 – передаточное число шестерни и колеса;

Z2 и Z1 – соответственно количество зубьев ведомого колеса и ведущей шестерни.

Как обозначается точность изготовления зубчатых колес

При изготовлении любые их виды имеют ряд погрешностей, среди которых выделяют четыре основные:

• кинематическую погрешность, связанную в основном с радиальным биением зубчатых венцов;
• погрешность плавности работы, вызываемую отклонениями шага и профиля зубьев;
• погрешность контакта зубьев в передаче, которая характеризует полноту прилегания их поверхностей в зацеплении;
• боковой зазор между неработающими поверхностями зубьев.

Для контроля первых трех погрешностей стандартами установлены специальные показатели – степени точности от 1 до 12, причем точность изготовления увеличивается с уменьшением показателя. Для контроля четвертой погрешности изготовления имеются два показателя:

• вид сопряжения зубчатых колес – обозначается литерами A, B, C, D, E, H;
• допуск на боковой зазор – обозначается литерами x, y, z, a, b, c, d, e, h.

Для обоих показателей бокового зазора обозначения даны в порядке убывания его величины и допуска на него.

Условно точность зубчатых колес обозначается двумя способами. Если степень точности по первым трем погрешностям одинакова, то ставится один общий для них численный показатель степени точности, за которыми стоят литеры обозначения вида сопряжения и допуска на боковой зазор. Например:

8-Ас ГОСТ 1643 – 81.

Если точности по первым трем погрешностям разные, то в обозначении ставятся три численных показателя последовательно. Например:

5-4-3-Са ГОСТ 1643 – 81.

Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

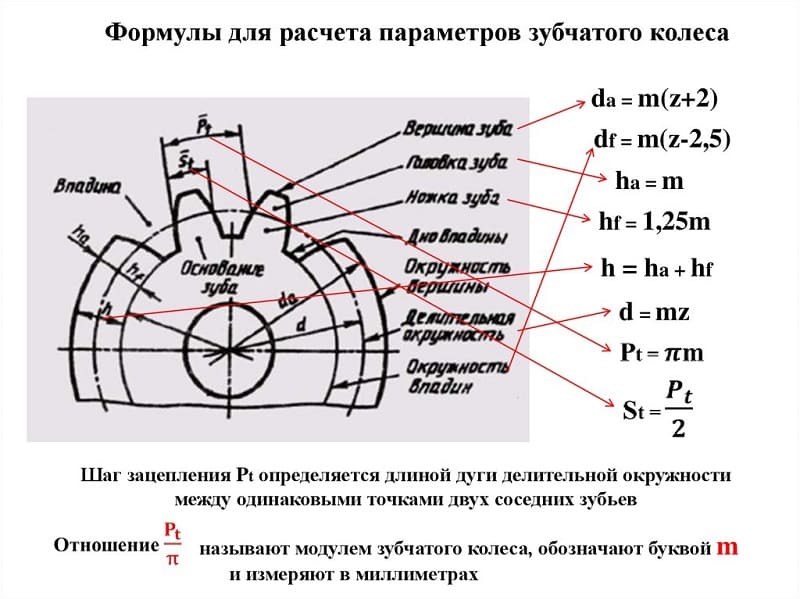
Расчет модуля зубчатого колеса

Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

π×D=t×z,

проведя преобразование, получим:

D=(t /π)×z

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

t/π=m,

размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:

В=m×z;

выполнив преобразование, находим:

m=D / z.

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов D_e получается равным

De=d+2× h’,

где h’- высота головки.

Высоту головки приравнивают к m:

 h’=m.

Проведя математические преобразования с подстановкой, получим:

De=m×z+2m = m(z+2),

откуда вытекает:

m=De/(z+2).

Диаметр окружности впадин D_i соответствует D_e за вычетом двух высот основания зубца:

D_i=D-2h“,

где h“- высота ножки зубца.

Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

h’ = 1,25m.

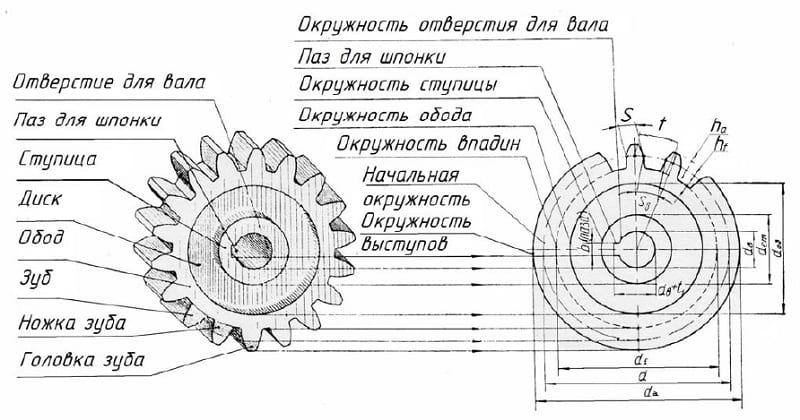
Устройство зубчатого колеса

Выполнив подстановку в правой части равенства, имеем:

D_i = m×z-2×1,25m = m×z-2,5m;

что соответствует формуле:

D_i = m(z-2,5m).

Полная высота:

h = h’+h“,

и если выполнить подстановку, то получим:

h = 1m+1,25m=2,25m.

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.

Следующий важный размер, толщину зубца s принимают приблизительно равной:

• для отлитых зубцов: 1,53m:
• для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины s_в, получаем формулы для ширины впадины

• для отлитых зубцов: s_в=πm-1,53m=1,61m:
• для выполненных путем фрезерования- s_в= πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

• усилия, прикладываемые к детали при эксплуатации;
• конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

Что представляет собой шестерня

Шестерня – это небольшое колесико с зубьями, которое крепится к специальной вращающейся оси. Поверхность у шестеренки в данном случае может быть как конической, так и цилиндрической.

Шестеренчатые передачи также имеют свою классификацию:

1. Прямозубые. Наиболее распространенный вид шестеренок, у которых зубья зачастую располагаются в радиальных плоскостях.
2. Скошенные. По-другому этот тип называется еще косозубым, а его использование в ходу у бензо- и электрических инструментов. По отношению к вращающейся оси они находятся под определенным углом.
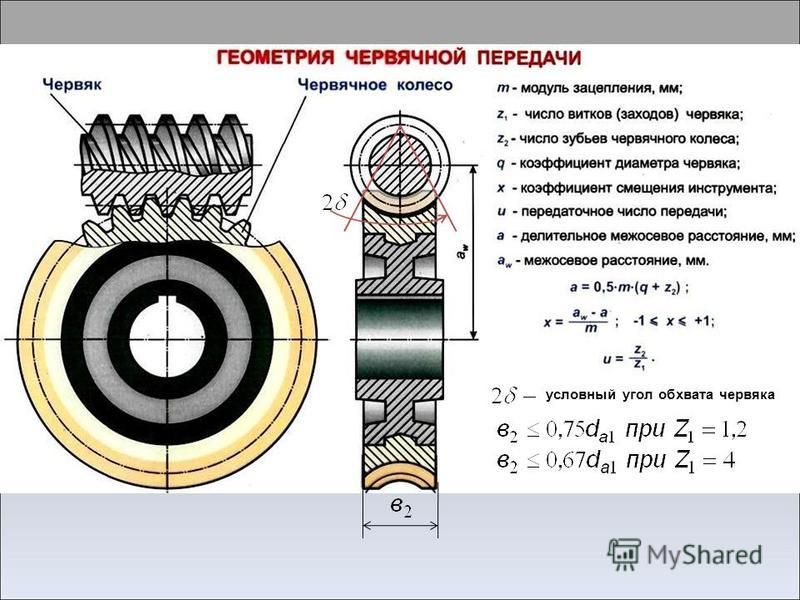
3. Червячные. Их еще называют спиральными шестернями, которые используются преимущественно для рулевого управления автомобилем.
4. Винтовые. Они имеют зачастую форму цилиндра, а также расположены по всей линии винта. Располагаются такие шестеренки на валах, которые расположены перпендикулярно к вращающейся оси.

Данные разновидности являются наиболее распространенными, однако далеко не единственными, поэтому используемый вид напрямую соотносится с тем, какую функцию он должен будет выполнять.

При этом каждая шестеренка имеет определенное количество зубьев, что определяется ее назначением. Разница между количеством используемых зубьев необходима, поскольку благодаря этому фактору появляется возможность регулировать обороты вала и крутящийся момент. Шестеренки также разделяются на ведущие и ведомые. Ведущей называется та шестерня, к которой вращательный момент подводится снаружи, а ведомой – та, с которой она снимается.

Почему шестеренку называют так?

Технически это понятно. Изначально «шестерёнка» — самое маленькое колесо в зубчатой передаче. Меньше шести зубьев там не бывает даже в теории, захват не обепечивается. … В машиностроении ведомое колесо зубчатой передачи редуктора называется колесом».

Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

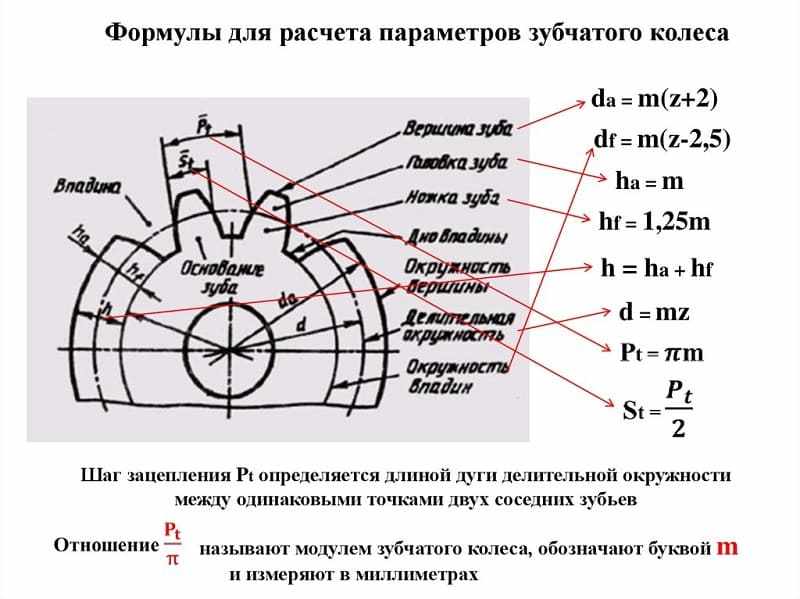
Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

π×D=t× z,

проведя преобразование, получим:

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:

выполнив преобразование, находим:

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов D e получается равным

где h’- высота головки.

Высоту головки приравнивают к m:

Проведя математические преобразования с подстановкой, получим:

De=m×z+2m = m(z+2),

откуда вытекает:

Диаметр окружности впадин D i соответствует D e за вычетом двух высот основания зубца:

где h“- высота ножки зубца.

Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

Выполнив подстановку в правой части равенства, имеем:

D i = m×z-2×1,25m = m×z-2,5m;

что соответствует формуле:

D i = m(z-2,5m).

Полная высота:

и если выполнить подстановку, то получим:

h = 1m+1,25m=2,25m.

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.

Следующий важный размер, толщину зубца s принимают приблизительно равной:

• для отлитых зубцов: 1,53m:
• для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины s в, получаем формулы для ширины впадины

• для отлитых зубцов: s в =πm-1,53m=1,61m:
• для выполненных путем фрезерования- s в = πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

• усилия, прикладываемые к детали при эксплуатации;
• конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

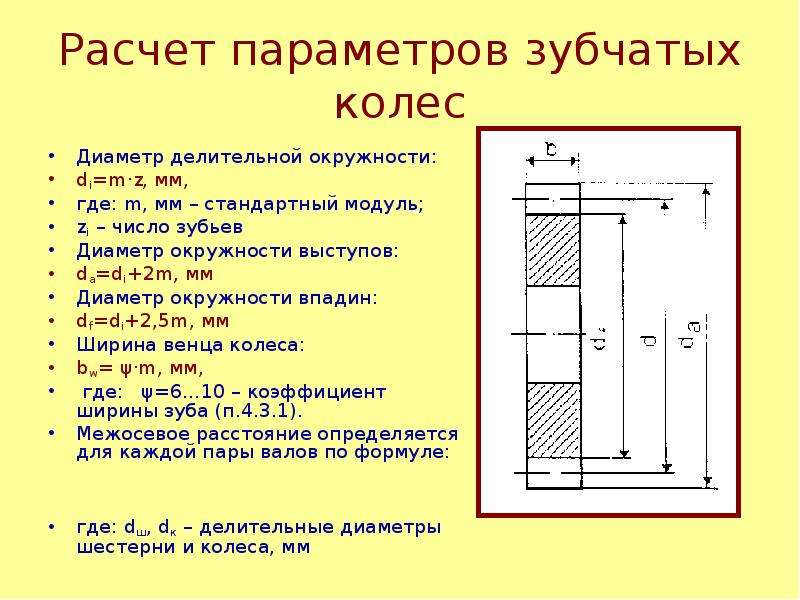
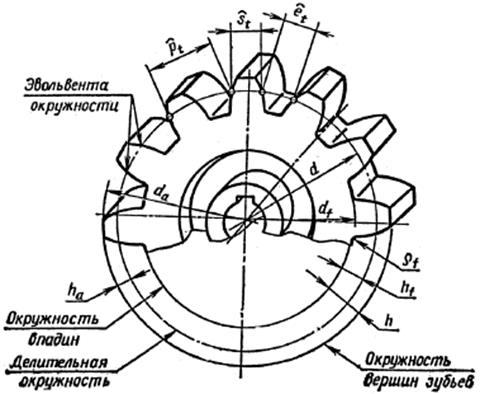
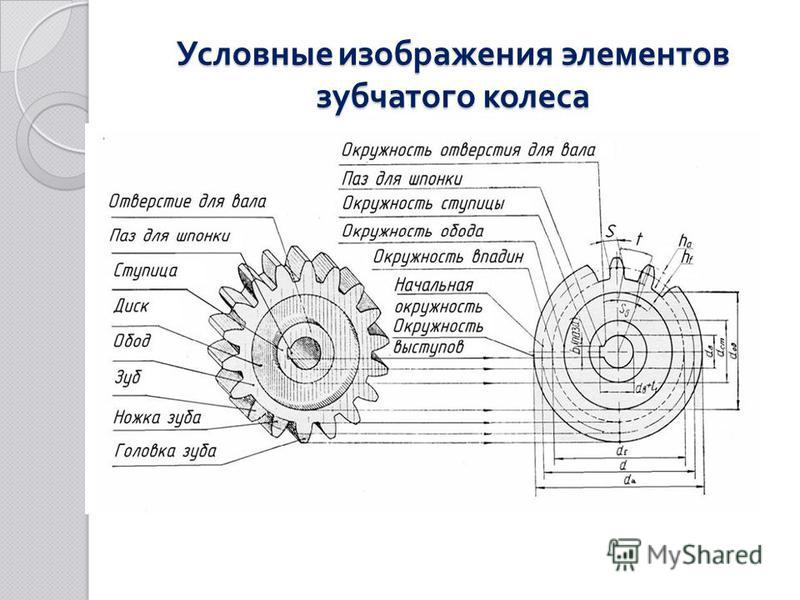
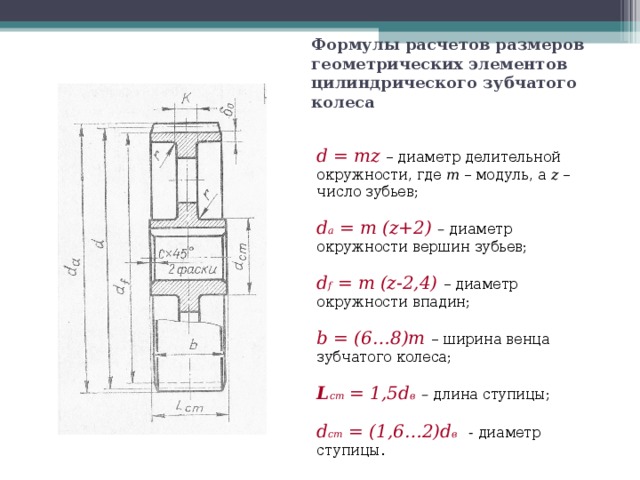
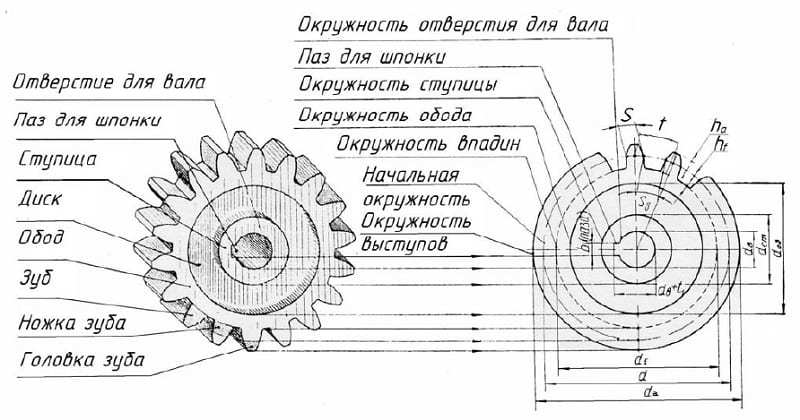
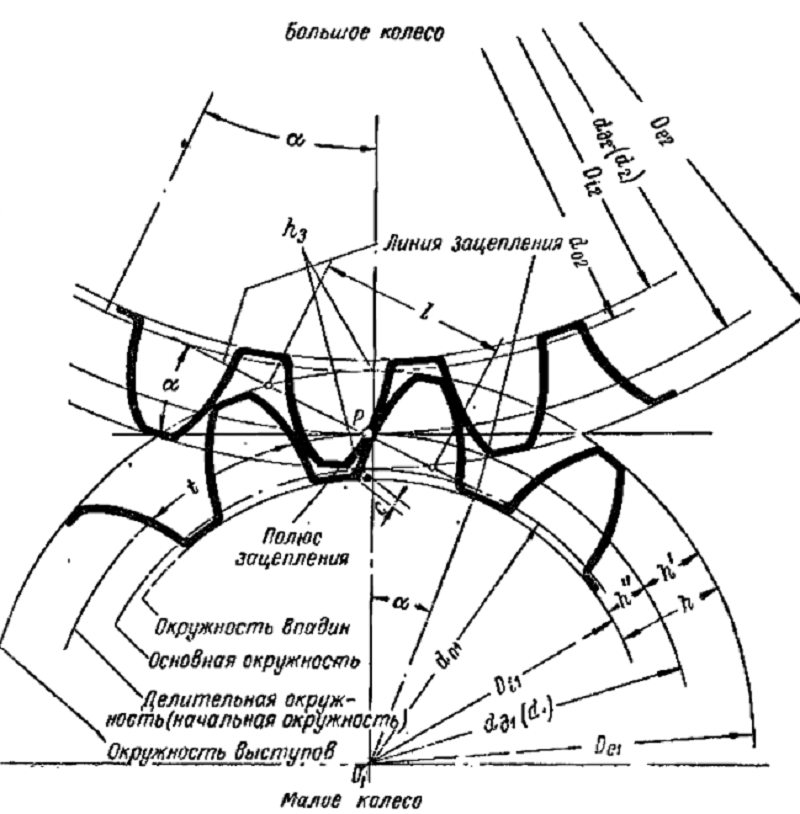
Диаметры окружностей

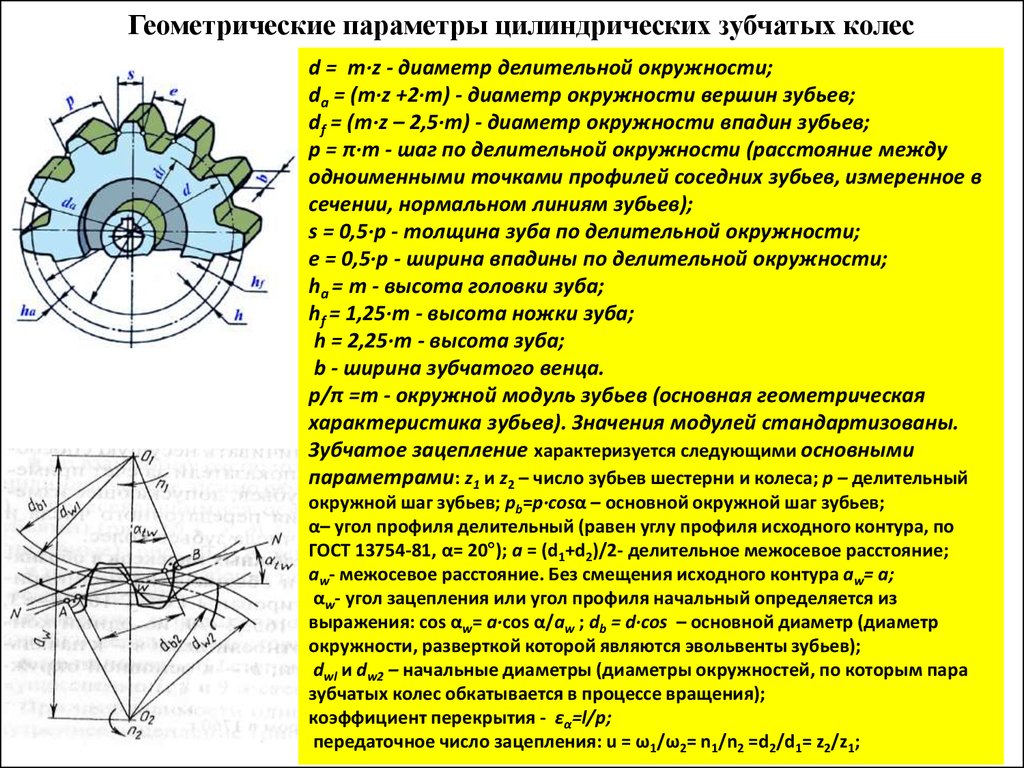
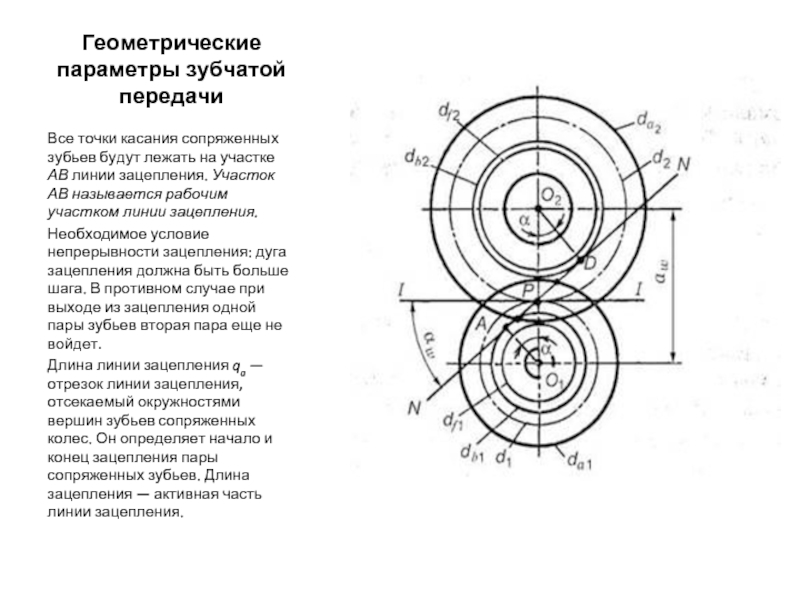
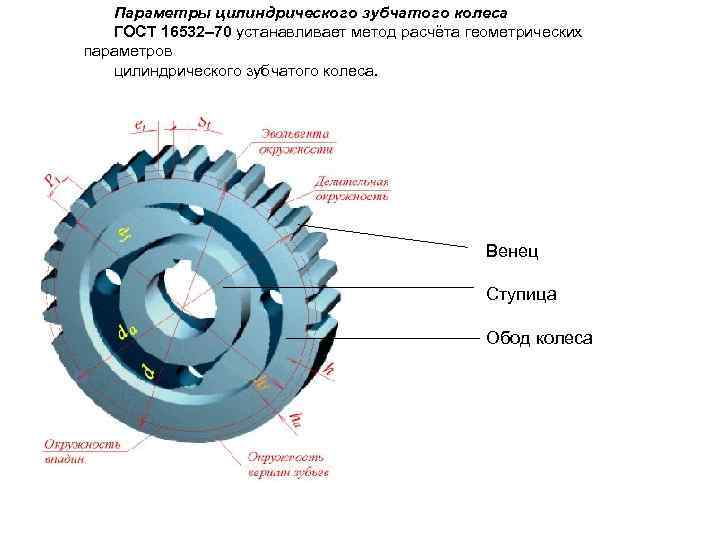
Рассмотрение геометрии зубчатых пар невозможно без определения диаметров. На каждой детали их выделяется несколько. Широкое распространение имеет диаметр окружности по выступам, иногда называемый диаметром вершин. Он определяет максимальные габариты диска колеса. Его противоположностью считается диаметр окружности впадин. Разность этих величин, поделенная пополам, дает полную длину зуба. Но этот параметр в чистом виде не используется. При расчетах принято выделять высоту головки и ножки зуба. Граница, отделяющая два этих понятия, называется делительной окружностью зубчатого колеса. Диаметр данной окружности выполняет функцию опорного параметра при выполнении расчетов геометрии, так как именно по ней определяется окружной шаг и модуль зацепления. Еще один диаметральный параметр, называемый основной окружностью, описывает теоретическую кривую, которая является базой при построении эвольвенты. Диаметр основной окружности используется для построения конкретного профиля зуба.

Особенности зубчатых колес и шестерен

И зубчатое колесо, и шестерня имеют вид диска с зубьями, расположенными на конической или цилиндрической поверхности. Эти детали используются в механизмах для преобразования и передачи крутящего момента. Изготовление шестерен и зубчатых колес возможно несколькими способами: методом обката, копированием, горячим и холодным накатыванием. Традиционно зубчатые колеса и шестерни используются парами, в зацеплении одна деталь становится ведущей, а вторая – ведомой. И вот здесь кроется главное различие элементов: ведущую деталь часто называют шестерней, а ведомую – зубчатым колесом. То есть разница основывается на роли элемента в работе механизма, но конструктивно шестерни и зубчатые колеса остаются одинаковыми деталями.

Также при парном зацеплении двух зубчатых колес шестерней называют ту деталь, которая имеет большее число зубьев. То, что зубчатые колеса и шестерни – понятия синонимичные, подтверждает и ГОСТ 16530-83: в определении шестерни указано, что она является ведущим зубчатым колесом передачи (при равном количестве зубьев на обеих деталях) или же колесом с меньшим числом зубьев.

Несмотря на это, некоторые специалисты (особенно работающие в специфических областях) считают необходимым строго разделять понятия шестерни и зубчатого колеса. Для них производство зубчатых колес и изготовление шестерен – принципиально разные процессы, а сами детали имеют свои сходства и различия.

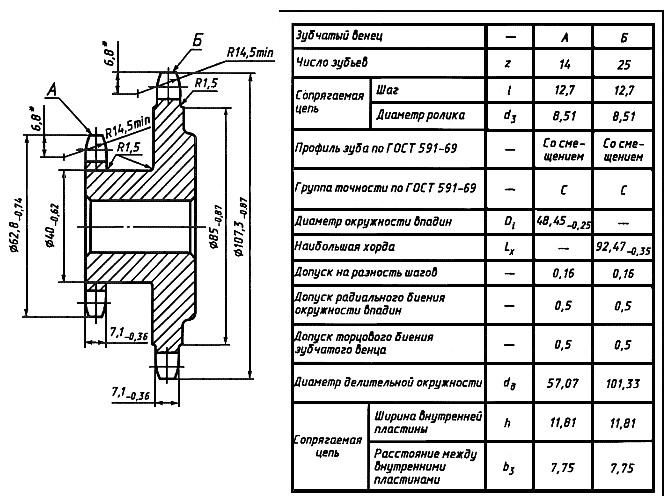
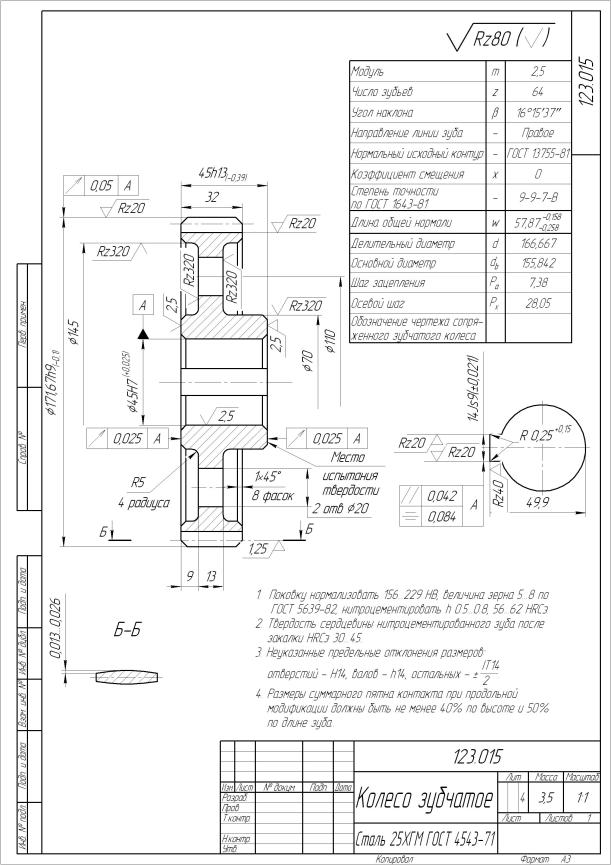
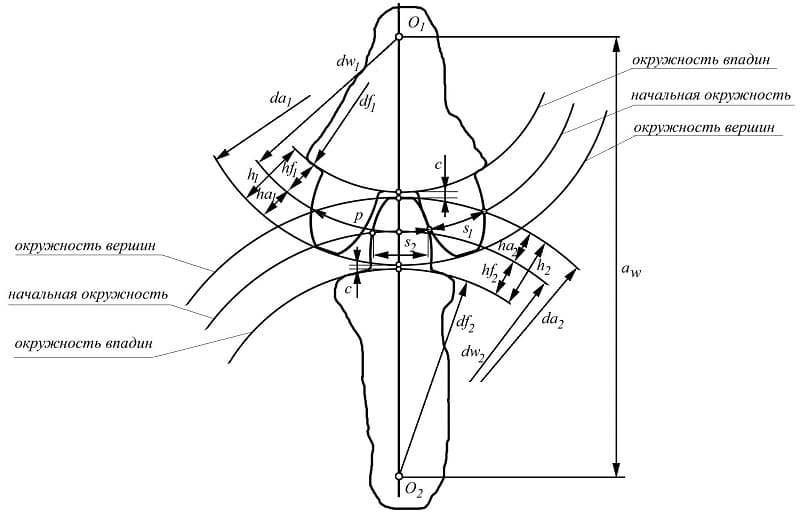
Основные параметры

Для обеспечения подвижности и работоспособности, конструкция отдельных деталей механической передачи должна быть согласована по размерам и геометрии. Для этого при описании подобных устройств принято использовать систему специальных параметров. В их число входят геометрические, массогабаритные и прочностные величины, закрепленные стандартами. Применение стандартных параметров позволяет сравнительно просто производить расчет унифицированных зубчатых передач и обеспечивает гарантированное сопряжение всех изделий между собой. Естественно, что для разных видов, параметры будут несколько отличаться. Далее рассматриваются термины, связанные с конструкцией эвольвентного цилиндрического колеса. Эти параметры, в своем большинстве, описывают основные характеристики и других вариантов колес.

В основе сечения зуба большинства шестерен лежит эвольвентный профиль, который  получается на основе одноименной кривой. Его применение легко стандартизируется,  характеризуется высокой технологичностью изготовления и низкими требованиями к качеству сборки механизма. Основными параметры эвольвентного зубчатого колеса  считаются модуль зацепления и количество зубьев зубчатого колеса. При одном и том же наружном диаметре деталей значения этих величин могут существенно отличаться в разных вариантах конструкции.

Число зубьев определяет коэффициент передачи и геометрические размеры зубьев. На ведущем колесе редуктора оно выполняется меньшим, чем на ведомом. В итоге один нормальный оборот ведущей шестерни приводит к повороту ведомого колеса только на определенный угол. Отношение числа зубьев двух колес  дает значение передаточного коэффициента. Размеры зубьев определяются как отношение их количества к длине окружности колеса. С целью упрощения расчетов и гарантированного обеспечения зацепления между разными колесами, предусмотрен дополнительный параметр, называемый модулем зацепления. Любые шестерни с одинаковым модулем обеспечивают взаимодействие между собой и могут использоваться для построения механизмов, без дополнительной обработки.

Сумма ширины зуба и впадины совместно дают шаг зубчатого колеса. Учитывая неравномерность профиля по радиусу и зависимость длины дуги от диаметра, в каждом колесе можно определить бесконечное число значений этого параметра. С целью стандартизации принято рассматривать шаг по делительной окружности, называемый так же окружным шагом. Отношение этого шага к числу пи дает модуль зацепления. В некоторых случаях для описания шестерен используют угловой шаг,  измеряемый в градусах. Стандартами предусмотрены и несколько других угловых величин. Например, для упрощения настройки оборудования при изготовлении колес рассматривают угловую ширину зуба и угловую ширину впадины. Определяются они также на основе делительной окружности.

Применение

Высокие свойства зубчатых передач нашли отражение в широком спектре применений. Во многих промышленных механизмах используются редукторы, призванные понизить  число оборотов вращения вала двигателя, для передачи на технологическое оборудование. Помимо изменения скорости, такое устройство также увеличивает механический момент. В итоге маломощный двигатель с большой скоростью вращения, способен приводить в движение медленный и тяжелый механизм.

С целью уменьшения габаритов редуктора его часто выполняют многоступенчатым. Большое количество зубчатых колес входят в последовательное зацепление между собой, обеспечивая высокое передаточное число. Классическим примером подобного устройства являются обычные механические часы. Благодаря множеству специально подобранных передач, скорости движения секундной, минутной и часовой стрелок отличаются друг от друга ровно в 60 раз.

Меняя один комплект на другой, можно получить разные скорости выходного вала. Этот принцип действия лег в основу коробок переключения передач, широко используемых в автомобилестроении, станкостроении и других отраслях.

Обычное зубчатое колесо допускает применение и для повышения скорости выходного вала относительно входного. В общем случае для этого достаточно развернуть редуктор или поменять местами точки подключения двигателя и конечного механизма.  Называется подобное устройство мультипликатор. Из особенностей его применения необходимо учитывать запас по мощности двигателя, сопоставимый с передаточным числом механизма.

Зубчатые колеса используются также  для изменения направления движения. Две цилиндрические шестерни с одинаковым числом зубьев реализуют функцию смены направления вращения вала. Передачи конической или корончатой конструкции используются в случае необходимости смены положения оси в пространстве. Ведущая и ведомая шестерни в таких механизмах развернуты друг относительно друга на какой-либо угол, значение которого может достигать 90 градусов. При этом передаточное отношение часто равно единице, что обеспечивает одинаковые скорости валов.

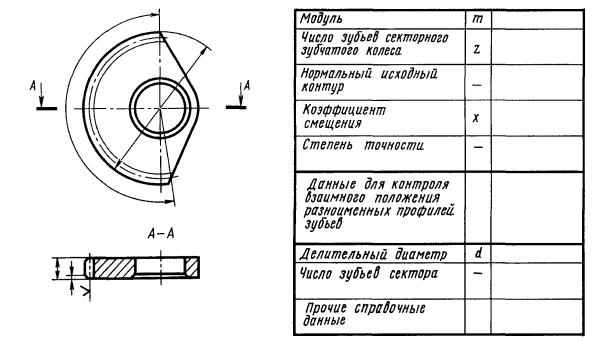
Наряду с простыми вариантами передач, содержащих зубчатые колеса, разработаны несколько специальных моделей. С целью снижения материалоемкости, в механизмах с ограниченным углом поворота, используют только часть зубчатого колеса. Такой сектор, обладая всеми основными свойствами зубчатого зацепления, отличается более низкой  массой и стоимостью.

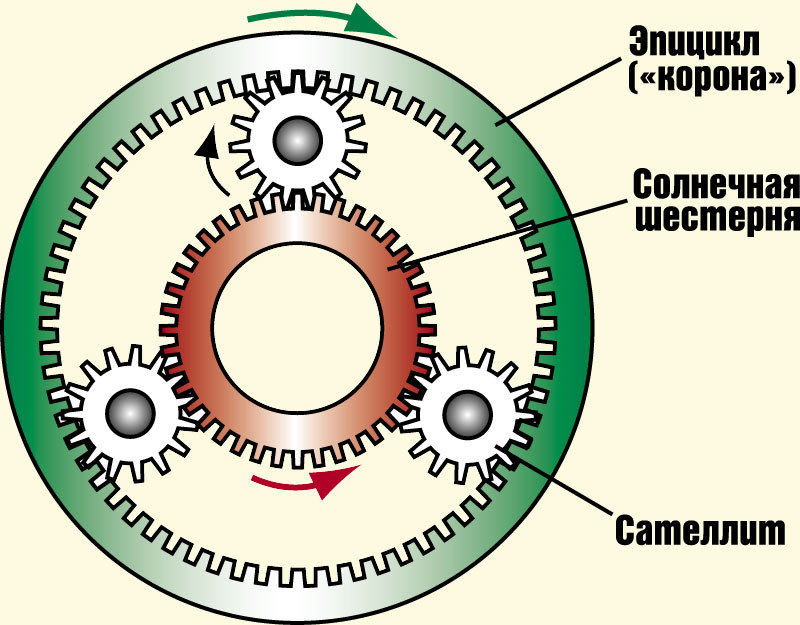
Еще один вариант, называемый планетарной передачей, также характеризуется малым весом и габаритами. При этом устройство обеспечивает высокое значение передаточного числа и пониженный уровень шума в процессе работы. Конструктивно такая передача состоит из нескольких шестерен, имеющих разную степень свободы. За счет этого механизм может не только передавать вращение, но и складывать или выделять угловые скорости разных валов, находящихся на одной оси. Сегодня разработано большое число вариантов планетарных передач,  отличающихся типом и взаимным расположением зубчатых колес. Планетарные передачи широко применяются в автомобильной и авиационной технике, тяжелом металлорежущем оборудовании. Среди недостатков, сдерживающих распространение передач данного типа, следует отметить низкий КПД и высокие конструктивные требования к точности изготовления отдельных деталей.

Исходные данные и замеры

На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.

Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.

Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.

Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.

Результаты расчетов

Для более крупных потребуются измерения и вычисления.

Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:

m=De/(z+2)

Последовательность действий следующая:

• измерить диаметр штангенциркулем;
• сосчитать зубцы;
• разделить диаметр на z+2;
• округлить результат до ближайшего целого числа.

Зубец колеса и его параметры

Данный метод подходит как для прямозубых колес, так и для косозубых.

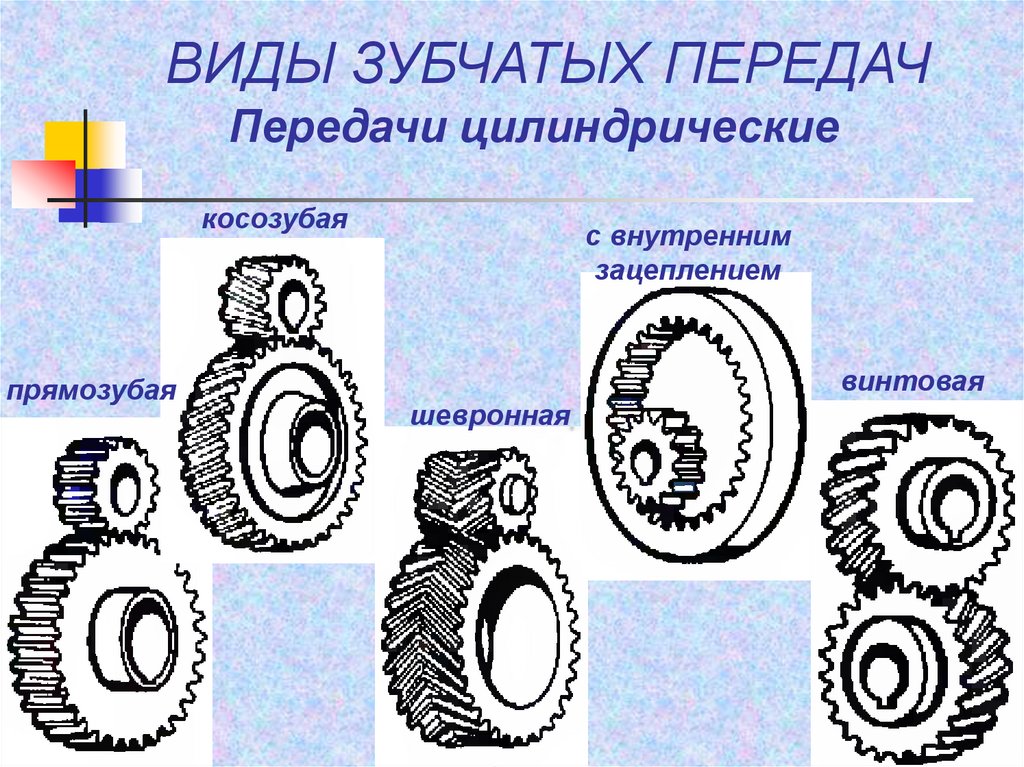
Цилиндрические зубчатые колеса (шестерни):

Цилиндрические зубчатые колеса используются в передачах, где оси валов располагаются параллельно относительно друг друга. При этом они могут располагаться как горизонтально, так и вертикально.

В зависимости от формы продольной линии зуба зубчатые колеса бывают: прямозубые, косозубые и шевронные.

Рис. 1. Цилиндрические зубчатые колеса: прямозубые, косозубые и шевронные

Прямозубое колесо. Этот вид шестерен ввиду своей простой конструкции является наиболее внедряемым в различных системах. В таком виде зубья шестерен располагаются в плоскости, которая перпендикулярна оси вращения. В отличии от косозубых и шевронных колес у данного вида предельный крутящий момент ниже.

Косозубое колесо. Зубья для данного вида колес выполняются под определенным углом к оси вращения шестерен, а по форме образуют часть винтовой линии. По сравнению с прямозубым колесом при работе зубьев данного вида зацепление зубьев происходит плавнее, а за счет увеличенной площади контакта предельный крутящий момент выше. Но для работы колес с косым зубом приходится применять упорные подшипники, так как возникает механическая сила, направленная вдоль оси. В основном косозубые колёса используются там, где нужны передачи большого крутящего момента на высоких скоростях.

Шевронное колесо. Этот вид имеет зубья, которые выполнены в форме буквы V на плоскости вращения колеса. Главной особенностью шевронных колес является то, что силы на осях обеих половин компенсируются, вследствие чего отпадает необходимость в использовании упорных подшипников. Различают шевронное и многошевронное цилиндрическое зубчатое колесо, состоящее соответственно из двух и более полушевронов, а также шевронное цилиндрическое зубчатое колесо со сплошным венцом и разделенными полушевронами.

В отдельные виды выделяются: цилиндрическое колесо с круговыми зубьями, цилиндрическое колесо со смещением (без смещения), циклоидальное, эвольвентное и цевочное цилиндрическое колеса.

Колесо с круговыми зубьями. Передачу с такими колесами называют передачей Новикова. При такой передаче контакт поверхностей зубьев происходит в одной точке на линии зацепления, расположенной параллельно осям колёс. Зубья данного вида колеса выполнены в виде полукруга, радиус которого подбирается под нужные требования. Колеса с круговыми зубьями в сравнении с косозубыми обладают более высокой нагрузочной способностью зацепления, высокой плавностью и бесшумностью работы, но при тех же условиях работы у них снижен КПД и ресурс работы, что не позволяет их применять широко.

Колесо со смещением либо без смещения. Это зубчатое колесо, зубья которого образованы при номинальном положении исходной производящей рейки, характеризуемом отсутствием касания (касанием) делительных поверхностей исходной производящей рейки и обрабатываемого зубчатого колеса.

Циклоидальное колесо. В данном виде профили зубьев шестерни выполнены по циклоидальной кривой. Однако при таком способе зацепления шестерен имеется большой недобор чувствительности из-за изменения расстояния между осями. Циклоидальное колесо  применяется в основном в приборостроении. Колесо сложно в изготовлении, поскольку при его создании требуется использование очень многих специальных зуборезных инструментов.

Цевочное колесо. В данном случае зубья одного из колес имеют вид пальцев в форме цилиндра. Такой вид шестерен образовался на базе циклоидального колеса и получил более широкое применение как в машиностроении, так и в приборостроении.

Применение механизма

Область применения подобных передач целесообразно рассматривать по трём наименованиям: скоростные, силовые, приборные. Все они получили широкое распространение в различных отраслях промышленности. Зубчатые колёса хорошо зарекомендовали себя при создании самых сложных кинематических схем.

Скоростные передачи предназначены для повышения скорости передаваемого вращения. Они успешно применяются в редукторах турбомашин, коробках перемены передач автомобилей (механических и автоматических).

От силовых передач требуется значительное повышение мощности передаваемого вращения. Они эксплуатируются в крановых установках, прокатных станах, тяговых механизмах различного назначения. Такие конструкции работают на малых скоростях. Благодаря этому удаётся передавать большие крутящие моменты. Главным требованием, которое предъявляют к элементам таких систем – плотный контакт между зубьями входящими в зацепление.

На практике распространение получил класс гипоидных агрегатов. Их устанавливают в механизмы и оборудование которые, используются в общем машиностроении. Например, грузовых и легковых автомобилях (в качестве элементов трансмиссии). Особое место такие системы занимают в вертолётостроении. Их применяют на летательных аппаратах практически всех конструкций. Этого удалось добиться благодаря применению зубчатых колёс оснащённых круговыми зубьями. Увеличением угла наклона зуба позволяет передаче работать более плавно. В этом случае удаётся избавиться от рывков и проскальзываний. Наиболее эффективным считается угол т равный 35°. Такие колеса обладают повышенной несущей способностью, надёжностью и долговечностью. Данные передачи работают плавно и практически бесшумно. Они надёжно выполняют свои функции, даже на высоких скоростях. Эта способность реализована благодаря многопарному зацеплению. Такой механизм позволяет снизить динамические нагрузки и предотвратить проскальзывание. Конструкции подобного вида активно применяются в приводе несущих винтов вертолетов различных аэродинамических схем.

Приборные или отсчетные устройства применяют в механизмах научно — исследовательских приборов, счетно-решающих устройствах, бытовой технике. Ведущие и ведомые элементы в этих устройствах могут изготавливаться из цветных металлов или синтетических и полимерных материалов.

В ней должны быть хорошо согласованы углы наклона ведущего и ведомого колеса, точно выверен угол поворота.

История

Сама по себе идея механической передачи восходит к идее колеса. Применяя систему из двух колёс разного диаметра, можно не только передавать, но и преобразовывать движение. Если ведомым будет большее колесо, то на выходе мы потеряем в скорости, но зато крутящий момент этой передачи увеличится. Эта передача удобна там, где требуется «усилить движение», например, при подъеме тяжестей. Но сцепление между передаточными колесами с гладким ободом недостаточно жесткое, колёса проскальзывают. Поэтому вместо гладких колес начали использовать зубчатые.

В Древнем Египте для орошения земель уже использовались приводимые в действие быками устройства, состоявшие из деревянной зубчатой передачи и колеса с большим числом ковшей.

Вместо зубьев первоначально использовали деревянные цилиндрические или прямоугольные пальцы, которые устанавливали по краю деревянных ободьев.

Изготовленный в I веке до н.э. Антикитерский механизм состоял из десятков металлических зубчатых колес .

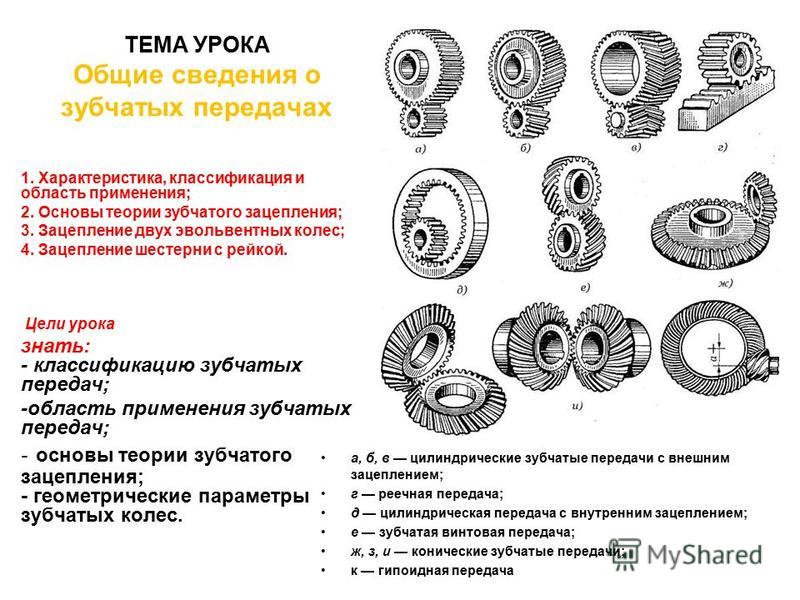
Типы зубчатых передач

Любое зубчатое колесо, независимо от его типа, делается и работает по одним и тем же вышеприведенным принципам. Однако различные их типы позволяют выполнить разные задачи. Некоторые виды передач обладают или высоким КПД, или высоким передаточным отношением, или же работают с непараллельными осями вращения шестерен, к примеру. Ниже приведены основные общие типы. Это не полный список. Также возможно и сочетание нижеприведенных типов.

Примечание: Приведены только типичные КПД передач. Из-за многих других возможных факторов приводимые КПД должны использоваться только в качестве справочных величин. Часто производители приводят ожидаемые КПД в паспортах для своих передач. Помните, что износ и смазка будут также существенно влиять на эффективность передач.

Сходства и различия шестерен и зубчатых колес

Придерживаясь вышеописанного мнения о разделении шестерен и зубчатых колес на два самостоятельных вида деталей, специалисты все же сходятся во мнении, что у этих элементов есть некоторые сходства:

• и шестерня, и зубчатое колесо могут выполнять функции как ведомого, так и ведущего элемента передачи (что противоречит терминологии межгосударственного стандарта);
• и та, и другая деталь может иметь коническую, либо цилиндрическую поверхность;
• оба элемента одинаково эффективны при эксплуатации в бензо- и электроинструменте;
• шестерни и зубчатые колеса можно использовать для запуска вращательных осей;
• эти виды деталей взаимозаменяемы, они схожи внешне и функционально.

Подобные сходства несколько противоречивы, но все же они встречаются в профессиональной среде. То же самое касается и различий, согласно которым:

• зубчатые колеса применяются только в сложных механизмах, в то время как шестерни являются универсальными элементами;
• шестерни используют исключительно парами, тогда как зубчатое колесо может работать без парного элемента;
• для зубчатых колес характерен больший диаметр, за счет чего эти детали чаще применяются в мощных системах.

Даже исходя из такой точки зрения можно сделать вывод, что шестерни и зубчатые колеса одинаковы по функционалу и в большинстве сфер не имеют формальной разницы.