Деформация кручения

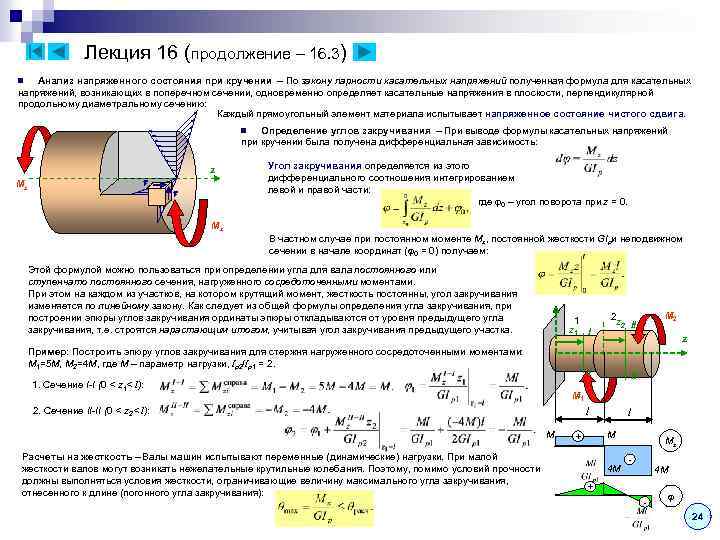
Измерение деформации

При проектировании и эксплуатации различных механизмов, технических объектов, зданий, мостов и других инженерных сооружений очень важно знать величину деформации материалов. Так как упругие деформации имеют маленькую величину, то измерения должны проводиться с очень высокой точностью

Для этого используют приборы, называемые тензометрами

Так как упругие деформации имеют маленькую величину, то измерения должны проводиться с очень высокой точностью. Для этого используют приборы, называемые тензометрами.

Тензометр состоит из тензометрического датчика и индикаторов. В него также может быть включено регистрирующее устройство.

В зависимости от принципа действия тензометры бывают оптические, пневматические, акустические, электрические и рентгеновские.

В основу оптических тензометров положено измерение деформации нити из оптоволокна, приклеенной к объекту исследования. Пневматические тензометры фиксируют изменение давления при деформации. В акустических тензометрах с помощью пьезоэлектрических датчиков проводятся измерения величин, на которые изменяются скорость звука и акустическое затухание при деформации. Электрические тензометры вычисляют деформацию на основе изменений электрического сопротивления. Рентгеновские определяют изменение межатомных расстояний в кристаллической решётке исследуемых металлов.

Вплоть до 80-х годов ХХ века сигналы датчиков регистрировались самописцами на обыкновенной бумажной ленте. Но когда появились компьютеры и начали бурно развиваться современные технологии, стало возможным наблюдать деформации на экранах мониторов и даже подавать управляющие сигналы, позволяющие изменить режим работы тестируемых объектов.

Чистый и поперечный изгиб балки

Если единственным внешним воздействием является сила, вызывающая изгибающий момент, такой изгиб называется чистым. Собственным весом изделия можно пренебречь.

При изгибе балки вводят следующие допущения:

• Во всех сечениях присутствуют только нормальные напряжения.
• Их разбивают на два слоя. Один называются растянутым, другой сжатым. Границей этих зон является линия сечения. Величина нормальных напряжений нейтрального слоя равны нулю.
• Продольный элемент детали подвержен осевому напряжению. Оно вызывает растяжение или сжатие. Соседние слои не вступают во взаимодействие друг с другом.
• При сохранении геометрической формы верхнего слоя все внутренние слои сохраняют прежнюю форму. Воздействие внешней силы остаётся перпендикулярным к поверхности детали.

Если на поверхность детали производится воздействие под углом к поверхности — такой изгиб называется поперечным. При поперечном изгибе в слоях детали (например, балки) возникают два вида напряжений. Одни называются нормальными, другие касательными. В этом случае все сечения не будут плоскими, но искривлёнными. На определённых уровнях искривления при изгибе не достаточно большие. Это позволяет при расчёте применять все формулы, справедливые для чистого изгиба.

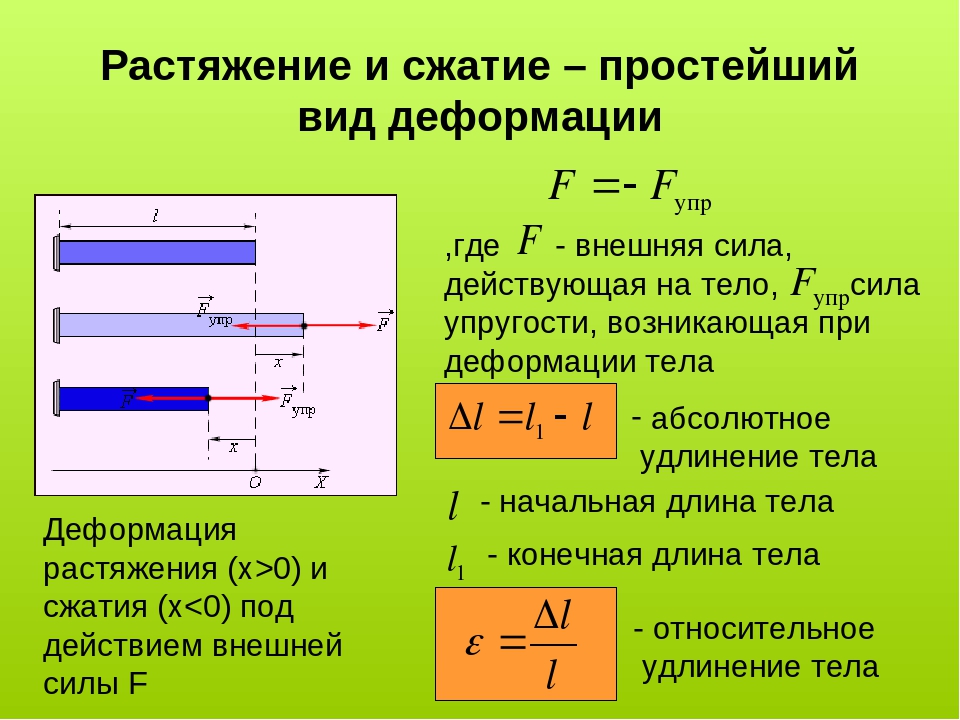
Закон Гука

Рассмотрим однородный стержень, имеющий длину l и площадь сечения S. К концам стержня приложены две силы равные по величине F, направленные по оси стержня, но в противоположные стороны. При этом длина стержня изменилась на величину .

Английским ученым Р. Гуком эмпирически было установлено, что для небольших деформаций относительное удлинение () прямо пропорционально напряжению ():

где E – модуль Юнга; – сила, которая действует на единичную площадь поперечного сечения проводника. Иначе закон Гука записывают как:

где k – коэффициент упругости. Для силы упругости, возникающей в стержне закон Гука имеет вид:

Линейная зависимость между и выполняется в узких пределах, при небольших нагрузках. При увеличении нагрузки зависимость становится нелинейной, а далее упругая деформация переходит в пластическую деформацию.

Это интересно: Деформация кручения — напряжение, определение, примеры, формула,

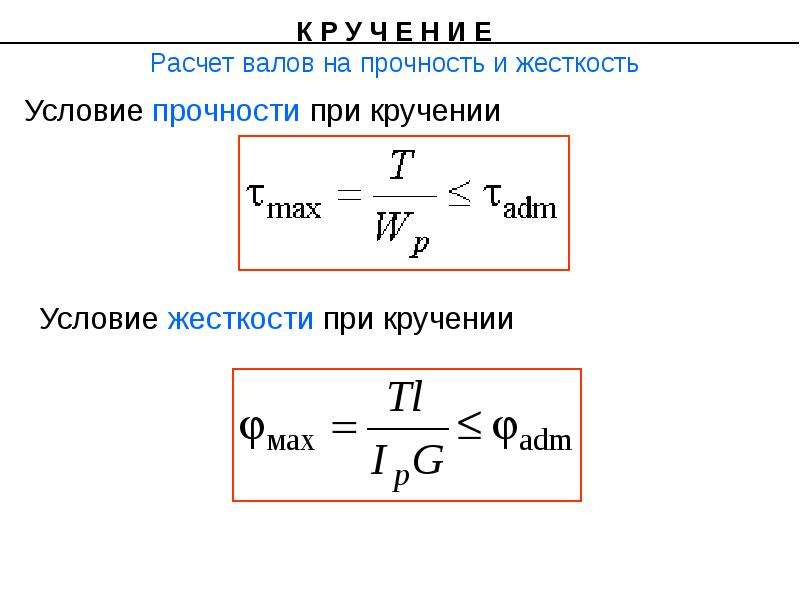
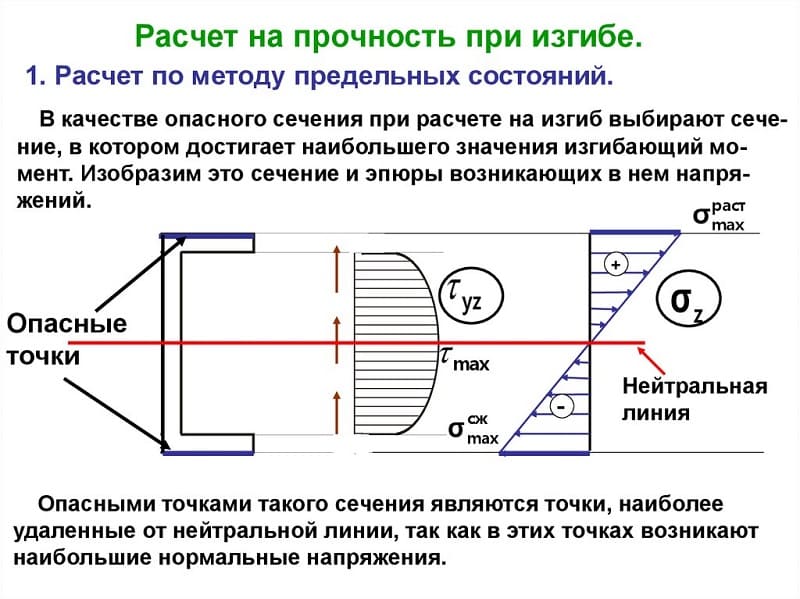
Расчёты на прочность при изгибе

Особую важность при проектировании конструкций и их отдельных элементов играют предварительные расчёты на прочность при возникающих изгибах. По результатам проведенных расчётов устанавливают фактические (реальные) и допустимые напряжения, которые способны выдержать элементы и вся конструкция в целом

Это позволит определить реальный срок службы разработать рекомендации по правильной эксплуатации разработанного объекта.

Условие прочности выводится в результате сравнения двух показателей. Наибольшего напряжения, которое возникает в поперечном сечении при эксплуатации и допустимого напряжения для конкретного элемента. Прочность зависит от применённого материала, размера детали, способа обработки и его физико-механических и химических свойств.

Для решения поставленной задачи применяются методы и математический аппарат, разработанный в дисциплинах техническая механика, материаловедение и сопротивление материалов. В этом случае применяются:

• дифференциальные зависимости Журавского (семейство дифференциальных уравнений связывающие основные параметры при деформации и их производные);
• способы определения перемещения (наиболее эффективными считаются метод Мора и правило Верещагина);
• семейство принятых гипотез;
• разработанные правила построения графических изображений (построение эпюр).

Расчёт параметров производится в три этапа:

• при проверочном расчёте (вычисляют величину максимального напряжения);
• на этапе проектирования (производится выбор толщины и параметров сечения бруса);
• во время вычисления допустимой нагрузки.

Полученные знаки величин напряжений определяются на основании оценки протекающих физических процессов и направления проекций векторов сил и моментов.

Наиболее наглядными результатами расчёта являются построенные эпюры на поверхности разрабатываемого изделия. Они отражают влияние всех силовых факторов на различные слои деталей. При чистом изгибе эпюры имеют следующие особенности:

• на участке исследуемой балки с отсутствием нагрузки, которая носит распределённый характер, эпюра изображается прямой линией;
• на участке приложения так называемых сосредоточенных сил на эпюре наблюдается изменение направления в форме скачка в том месте к которому приложен вектор силы;
• в точке появления приложенного момента, скачок равен величине этого параметра;
• на участке с распределённой нагрузкой интенсивность воздействия изменяется по линейному закону, а поперечные нагрузки носят степенной характер изменения (чаще всего по параболической кривой, с направлением выпуклости в сторону приложенной нагрузке);
• в границах исследуемого участка функция изгибающего момента приобретает экстремум (на основании методов исследования функций с помощью дифференциального исчисления можно установить характер экстремума – максимум или минимум).

На практике решение систем дифференциальных уравнений может вызвать определённые трудности. Поэтому при расчётах допускаются некоторые прощения, которые не влияют на точность определяемых параметров. К этим упрощениям относятся:

• расчёт производят с учётом нормальных напряжений;
• в качестве основного предположения принимают гипотезу о плоских сечениях;
• продольные волокна не производят дополнительного давления между собой (это позволяет считать, что процессы изгиба носят линейный характер);
• деформация волокон не зависит от их ширины (значения нормальных напряжений постоянные по всей ширине);
• для расчётной балки задают одну плоскость симметрии (все внешние силы лежат в этой плоскости);
• физико-механические характеристики материала подчиняются закону Гука (модуль упругости имеет постоянную величину);
• процессы в балке подчиняются законам плоского изгиба (это допущение вытекает из соотношений геометрических размеров изделия).

Современные методы исследования воздействия внешних сил, внутренних напряжений и моментов позволяют с высокой степенью точности рассчитать прочность каждой детали и всей конструкции в целом. Применение компьютерных методов расчёта, фрактальной геометрии и 3D графики позволяет получить подробную картину происходящих процессов.

Пластическая и упругая деформация

В процессе деформации важное значение имеет величина межатомных связей, приложение нагрузки достаточной для их разыва приводит к необратимым последствиям (необратимая или пластическая деформация). Если нагрузка не превысила допустимых значений, то тело может вернуться в исходное состояние (упругая деформация). Простейший пример поведения предметов, подверженных пластической и упругой деформацией, можно проследить на падении с высоты резинового мяча и куска пластилина

Резиновый мяч обладает упругостью, поэтому при падении он сожмется, а после превращения энергии движения в тепловую и потенциальную, снова примет первоначальную форму. Пластилин обладает большой пластичностью, поэтому при ударе о поверхность оно необратимо утратит свою первоначальную форму

Простейший пример поведения предметов, подверженных пластической и упругой деформацией, можно проследить на падении с высоты резинового мяча и куска пластилина. Резиновый мяч обладает упругостью, поэтому при падении он сожмется, а после превращения энергии движения в тепловую и потенциальную, снова примет первоначальную форму. Пластилин обладает большой пластичностью, поэтому при ударе о поверхность оно необратимо утратит свою первоначальную форму.

За счет наличия деформационных способностей все известные материалы обладают набором полезных свойств – пластичностью, хрупкостью, упругостью, прочностью и другими. Исследование этих свойств достаточно важная задача, позволяющая выбрать или изготовить необходимый материал. Кроме того, само по себе наличие деформации и его детектирование часто бывает необходимо для задач приборостроения, для этого применяются специальные датчики называемые экстензометрами или по другому тензометрами.

Виды деформации твердых тел

Деформация растяжения

Деформация растяжения — вид деформации, при которой нагрузка прикладывается продольно от тела, то есть соосно или параллельно точкам крепления тела. Проще всего растяжение рассмотреть на буксировочном тросе для автомобилей. Трос имеет две точки крепления к буксиру и буксируемому объекту, по мере начала движения трос выпрямляется и начинает тянуть буксируемый объект. В натянутом состоянии трос подвергается деформации растяжения, если нагрузка меньше предельных значений, которые может он выдержать, то после снятия нагрузки трос восстановит свою форму.

Схема растяжения образца

Посмотрите прибор измеряющий деформацию растяжения →

Деформация растяжения является одним из основных лабораторных исследований физических свойств материалов. В ходе приложения растягивающих напряжений определяются величины, при которых материал способен:

1. воспринимать нагрузки с дальнейшим восстановлением первоначального состояния (упругая деформация)
2. воспринимать нагрузки без восстановления первоначального состояния (пластическая деформация)
3. разрушаться на пределе прочности

Данные испытания являются главными для всех тросов и веревок, которые используются для строповки, крепления грузов, альпинизма. Растяжение имеет значение также при строительстве сложных подвесных систем со свободными рабочими элементами.

Деформация сжатия

Деформация сжатия — вид деформации, аналогичный растяжению, с одним отличием в способе приложения нагрузки, ее прикладывают соосно, но по направлению к телу. Сдавливание объекта с двух сторон приводит к уменьшению его длины и одновременному упрочнению, приложение больших нагрузок образовывает в теле материала утолщения типа «бочка».

Схема сжатия образца

В качестве примера можно привести тот же прибор что и в деформации растяжения немного выше.

Деформация сжатия широко используется в металлургических процессах ковки металла, в ходе процесса металл получает повышенную прочность и заваривает дефекты структуры

Сжатие также важно при строительстве зданий, все элементы конструкции фундамента, свай и стен испытывают давящие нагрузки. Правильный расчет несущих конструкций здания позволяет сократить расход материалов без потери прочности

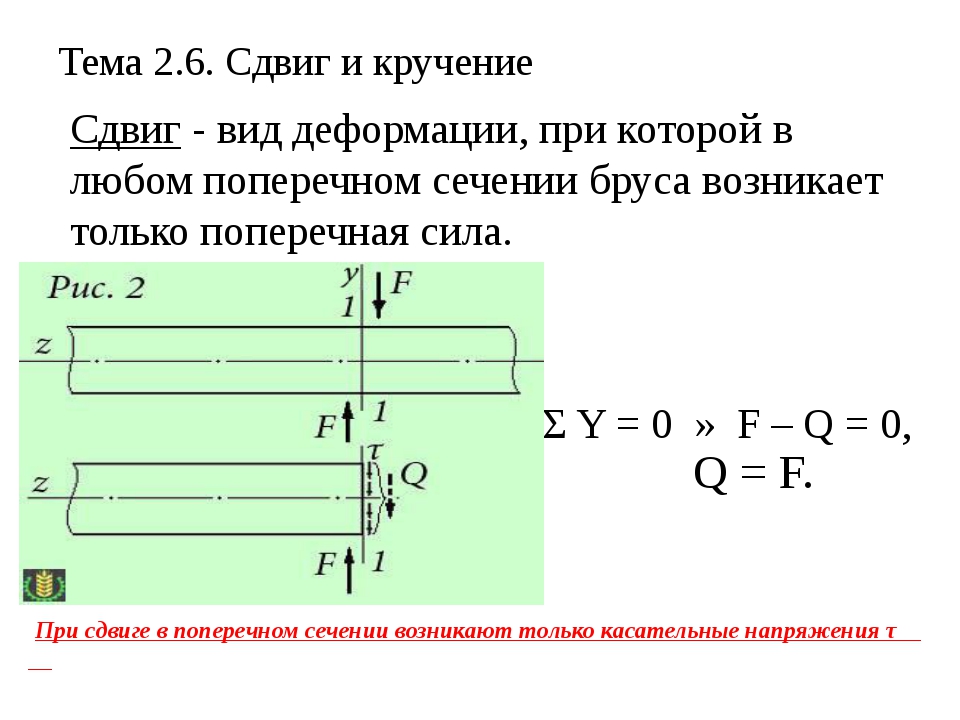
Деформация сдвига

Деформация сдвига — вид деформации, при котором нагрузка прикладывается параллельно основанию тела. В ходе деформации сдвига одна плоскость тела смещается в пространстве относительно другой. На предельные нагрузки сдвига испытываются все крепежные элементы — болты, шурупы, гвозди. Простейший пример деформации сдвига – расшатанный стул, где за основание можно принять пол, а за плоскость приложения нагрузки – сидение.

Схема сдвига образца

Посмотрите прибор измеряющий деформацию сдвига →

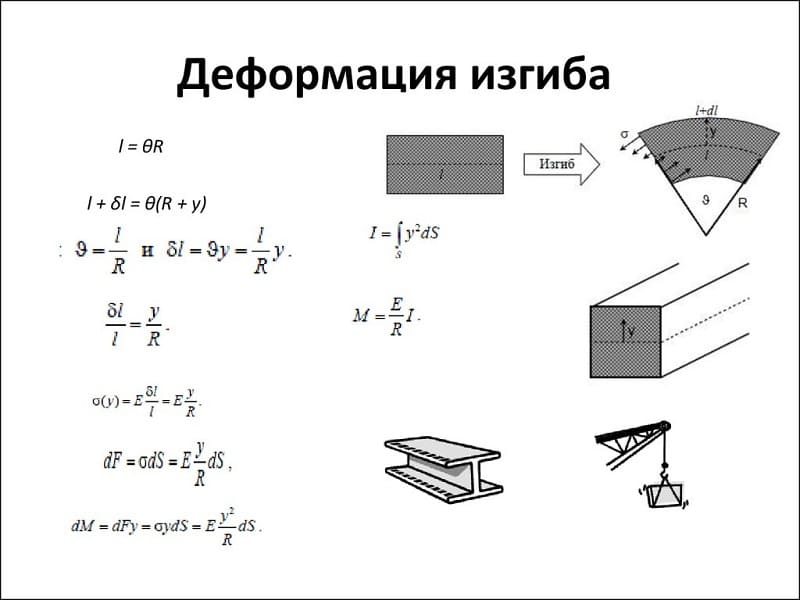
Деформация изгиба

Деформация изгиба — вид деформации, при котором нарушается прямолинейность главной оси тела. Деформации изгиба испытывают все тела подвешенные на одной или нескольких опорах. Каждый материал способен воспринимать определенный уровень нагрузки, твердые тела в большинстве случаев способны выдерживать не только свой вес, но и заданную нагрузку. В зависимости от способа приложения нагрузки при изгибе различают чистый и косой изгиб.

Схема изгиба образца

Посмотрите прибор измеряющий деформацию изгиба →

Значение деформации изгиба важно для проектирования упругих тел, таких, как мост с опорами, гимнастический брус, турник, ось автомобиля и другие

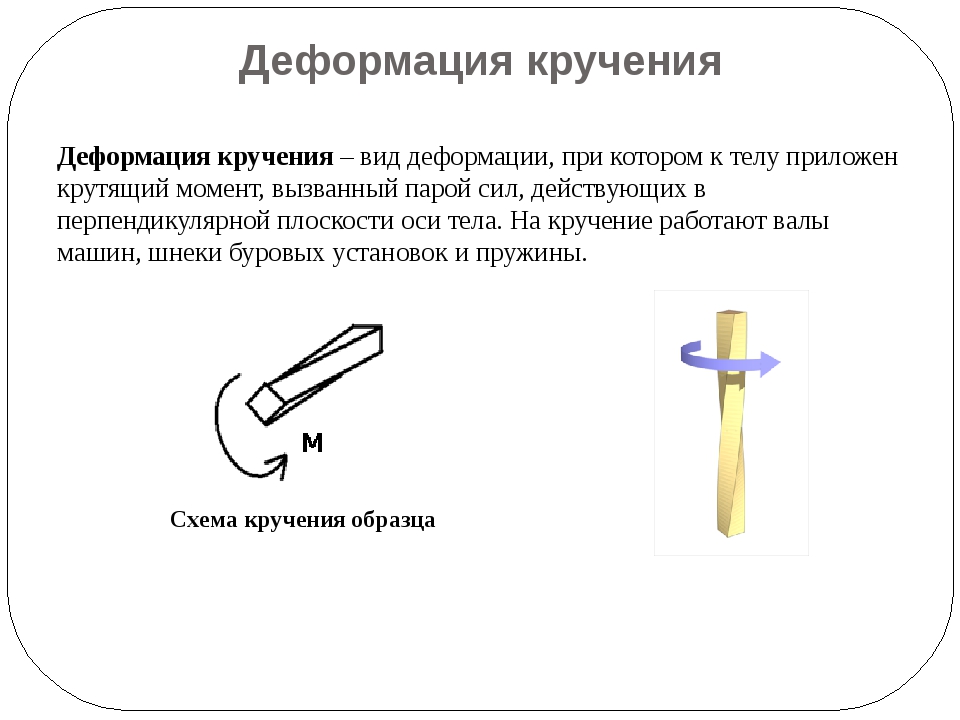
Деформация кручения

Деформация кручения – вид деформации, при котором к телу приложен крутящий момент, вызванный парой сил, действующих в перпендикулярной плоскости оси тела. На кручение работают валы машин, шнеки буровых установок и пружины.

Схема кручения образца

Посмотрите прибор измеряющий деформацию кручения →

Основные понятия

Под изгибом детали понимают естественное или искусственное изменение формы. Этот процесс разделяется на две категории – плоский или косой. В первом случае ось детали сохраняет своё первоначальное положение, во втором происходит её изменение в горизонтальной или вертикальной плоскости.

Основным теоретическим положением, определяющим физические процессы, протекающие в результате изгиба, является закон Гука. Согласно ему величина деформации (изгиба), пропорциональна приложенной к этому телу силе. Для каждого из видов деформации разработан индивидуальный расчёт действующих характеристик.

Оценка степени влияния действующих факторов на деформацию осуществляется с помощью следующих показателей:

• площади поверхности подверженной деформации;
• длины детали;
• силы, воздействующие на конструкцию;
• модуль упругости (его абсолютный показатель);
• величина и характер изменения модуля длины в результате упругой деформации.

Одним из важных параметров считается потенциальная энергия деформации при изгибе. На основании этих параметров производят определение модуля Юнга. С его помощью рассчитывают скорость распространения продольной волны. Величина механического напряжения, при которой деформация тела всё ещё будет упругой, а сам объект способен восстановить первоначальную форму после снятия нагрузки, называется пределом упругости. При превышении допустимого значения этого параметра тело начнёт разрушаться. Этот предел называется прочностью. При оценке прочностных показателей применяют следующие предположения:

1. О постоянстве нормальных напряжений. Она определяет постоянство расстояний при возникновении напряжений изгиба.
2. Плоскости сечений. Оно называется гипотезой Бернулли. Сечения детали в спокойном положении находятся в плоском состоянии. После деформации они сохраняют первоначальную форму, но разворачиваются относительно некоторой линии. Она называется нейтральной осью.
3. Отсутствие давлений на боковые поверхности. Считается, что соседние волокна не оказывают давления друг на друга.

Перечисленные гипотезы позволяют оценить деформации сдвига и характер изгиба каждого слоя исследуемой детали. Это происходит в результате воздействия различных сил. Нагрузки вызывают деформацию изгиба в различных плоскостях. Они подразделяются на две категории:

• характеру воздействия (статические или динамические);
• степени воздействия (массовые или объёмные);
• поверхности (сосредоточенные, воздействуют на отдельные элементы поверхности и распределёнными – на всю поверхность).

К статическим относятся нагрузки, у которых место приложения и направления сил не меняется или изменяются медленно в течение определённого промежутка времени. К таким нагрузкам относится сила тяжести. В этом случае можно принять утверждение, что элементы физического объекта находятся в состоянии равновесия. У динамических нагрузок эти параметры меняются достаточно быстро или носят импульсивный характер. К ним относятся ударные нагрузки при забивании свай, обработке металла ковкой, воздействие неровностей дороги на колесо.

При сосредоточенной статической нагрузке на отдельный участок поверхности бруса происходит его деформация в сторону по направлению сил взаимодействия. Для расчёта параметров характеризующих основные показатели состояния деформированного тела применяют дифференциальные уравнения, которые позволяют выявить существующие функциональные связи. По деформации изгиба с помощью модуля Юнга можно вычислить прочность исследуемого элемента конструкции (балки, бруса, подвесной опоры и т. д.). На основании полученных областей решения можно построить графическое изображение силы упругости, которое наглядно показывает, что происходит с различными участками деформированной детали. Для каждой детали в зависимости от её геометрических размеров, материала изготовления и величины приложенных сил выведена своя формула.

Для наглядности восприятия характера протекающих процессов использует метод нанесения эпюр на поверхность объекта. Эта операция называется топология. Основной идеей является проецирование линий нагрузки на соответствующую плоскость (горизонтальную, фронтальную или профильную). В современных методах топологии применяют фрактальную геометрию.

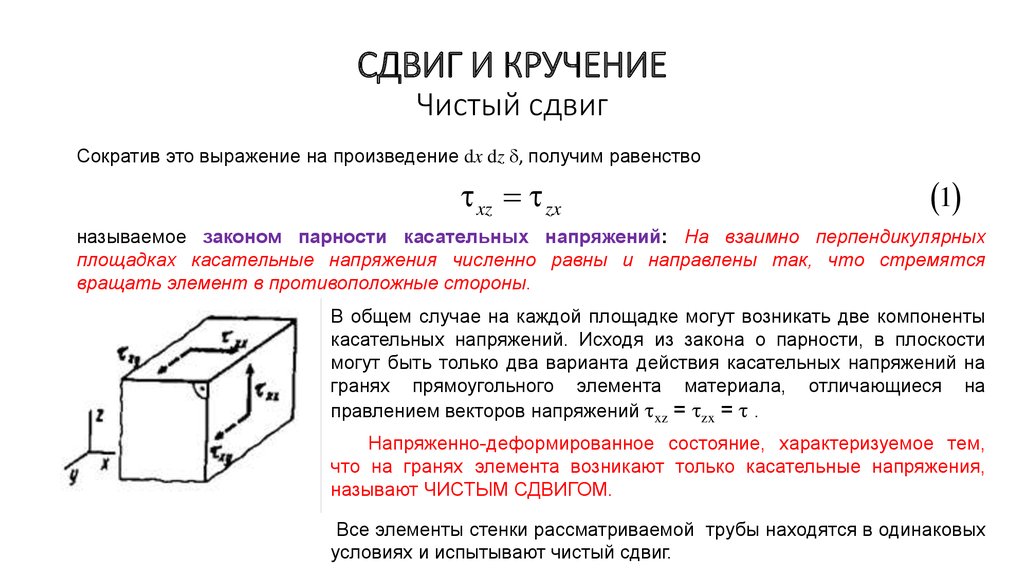
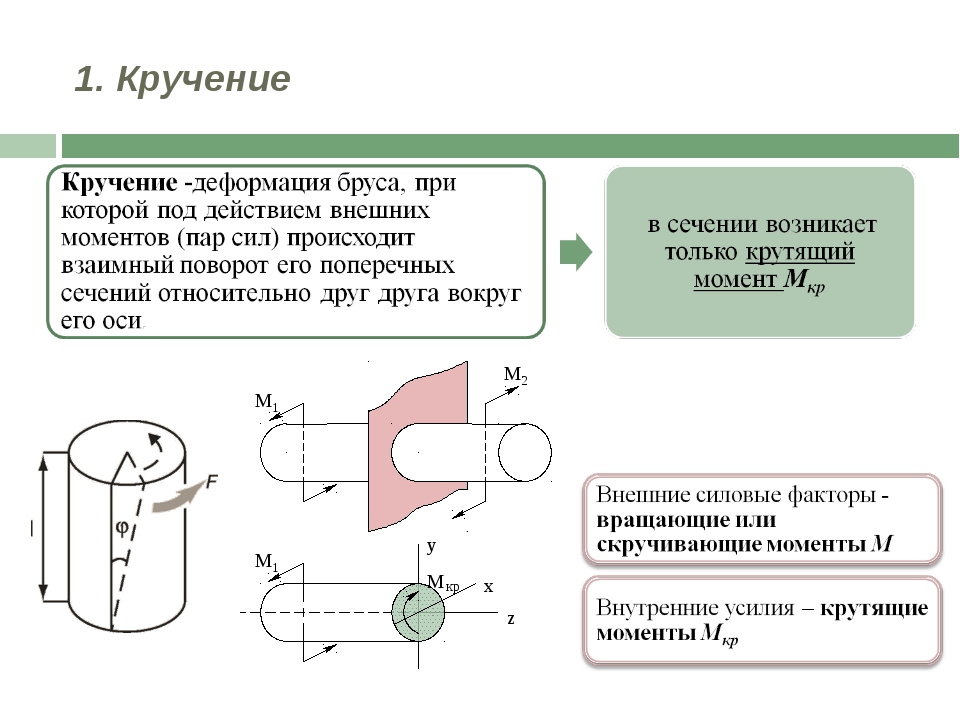
Кручение

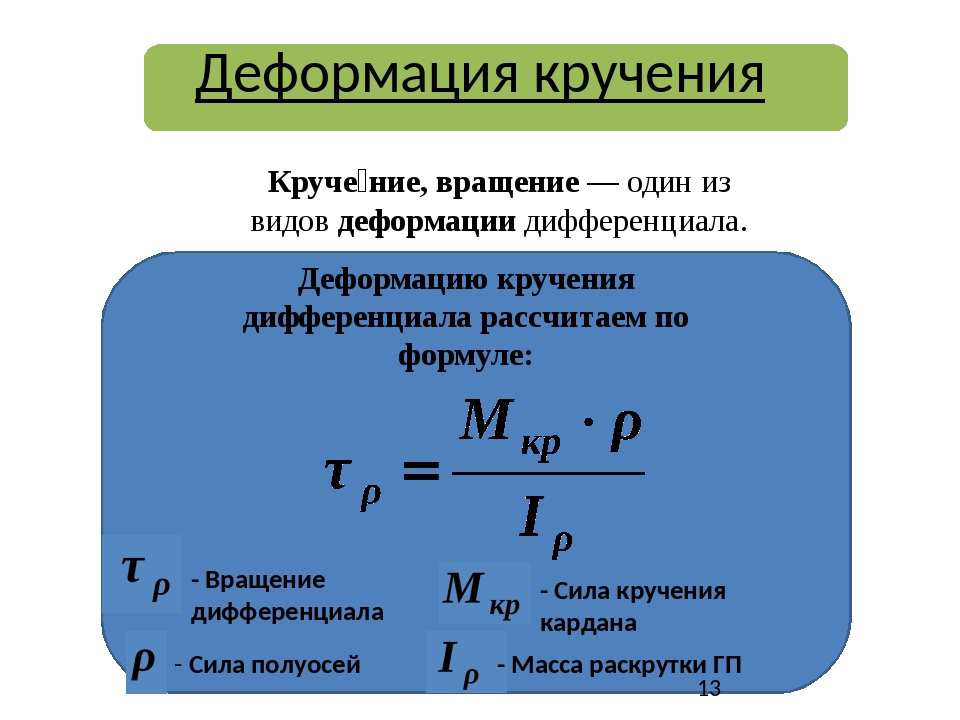
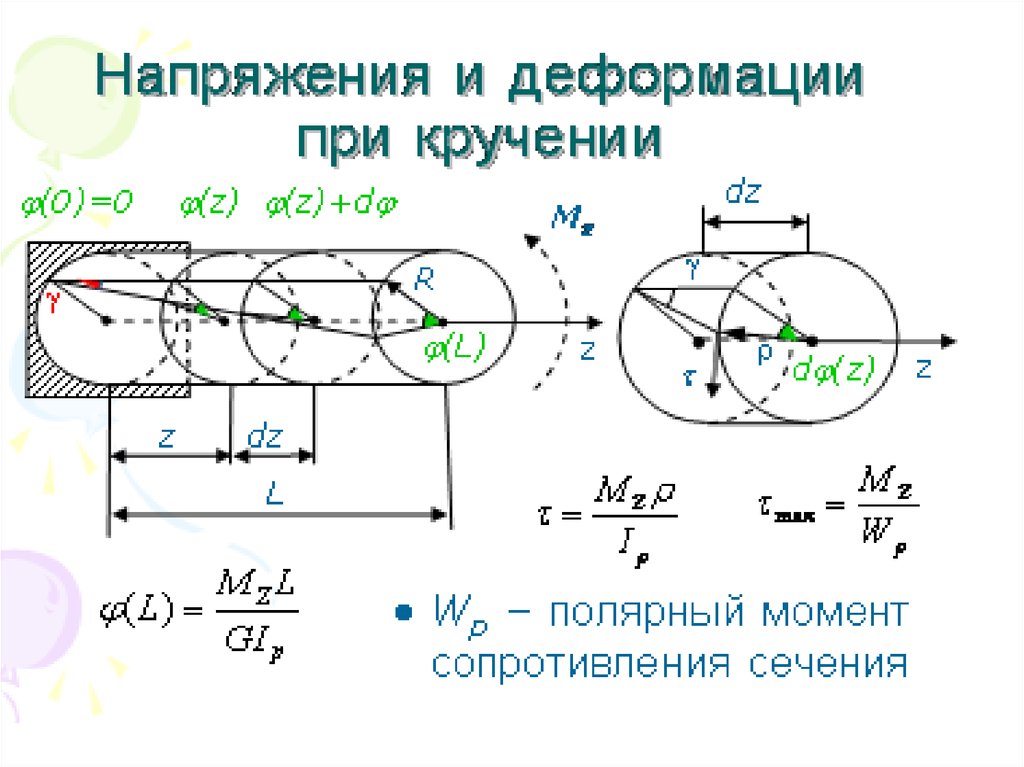
Кручение — один из видов деформации тела. Возникает в том случае, если нагрузка прикладывается к телу в виде пары сил (момента) в его поперечной плоскости. При этом в поперечных сечениях тела возникает только один внутренний силовой фактор — крутящий момент. На кручение работают пружины растяжения-сжатия и валы. При деформации кручения смещение каждой точки тела перпендикулярно к её расстоянию от оси приложенных сил и пропорционально этому расстоянию.

Деформацию кручения можно наблюдать, если на стержень, один конец которого закреплен, действует пара сил, лежащих в плоскости, перпендикулярной оси стержня. При кручении отдельные слои тела остаются параллельными, но поворачиваются друг относительно друга на некоторый угол. Деформация кручения представляет собой неравномерный сдвиг. Деформации кручения возникают при завинчивании гаек, при работе валов машин.

Пример деформации кручения цилиндрического стержня

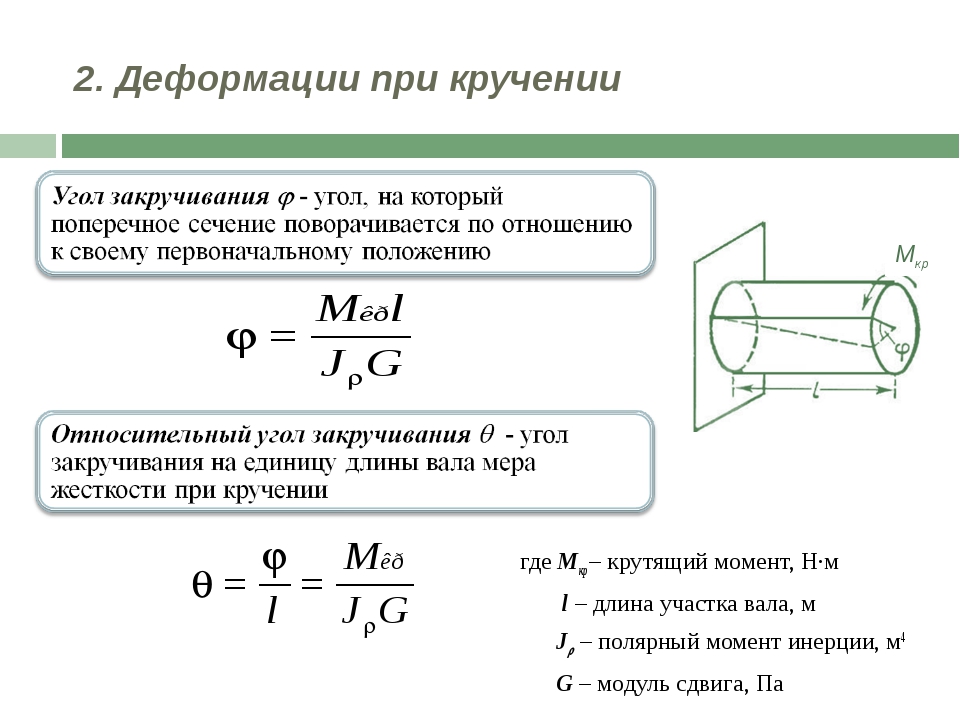
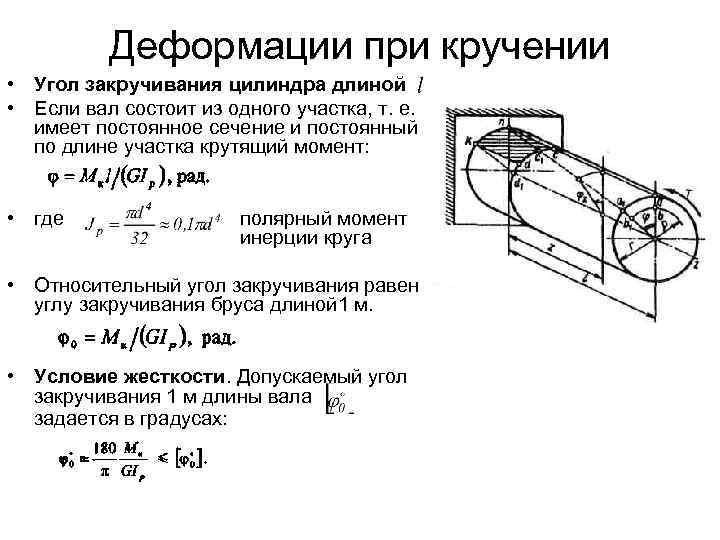
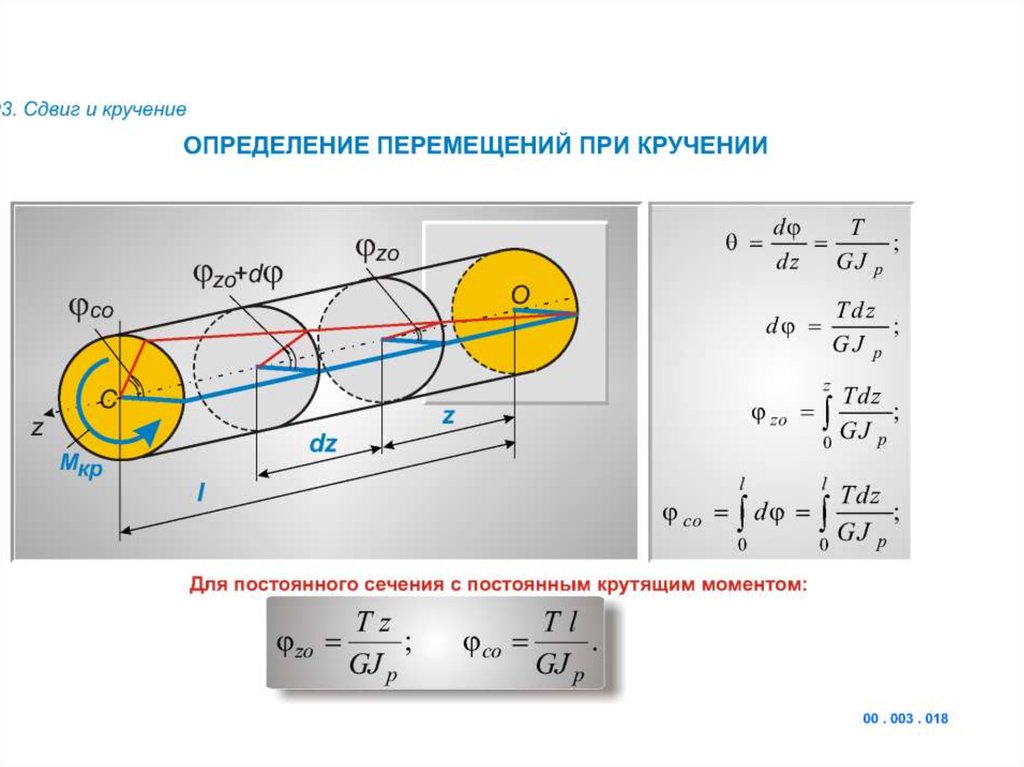
Если проволоку или стержень, закрепленные с одного конца, закручивать, прилагая к другому концу пару сил F с моментом, равным М, то стержень (проволока) претерпевает деформацию кручения, при которой одно его основание поворачивается по отношению к другому, фиксированному, на некоторый угол φ – угол кручения (рис. 1; 2).

Рис. 1.

Отношение угла закручивания φ к длине называют относительным углом закручивания

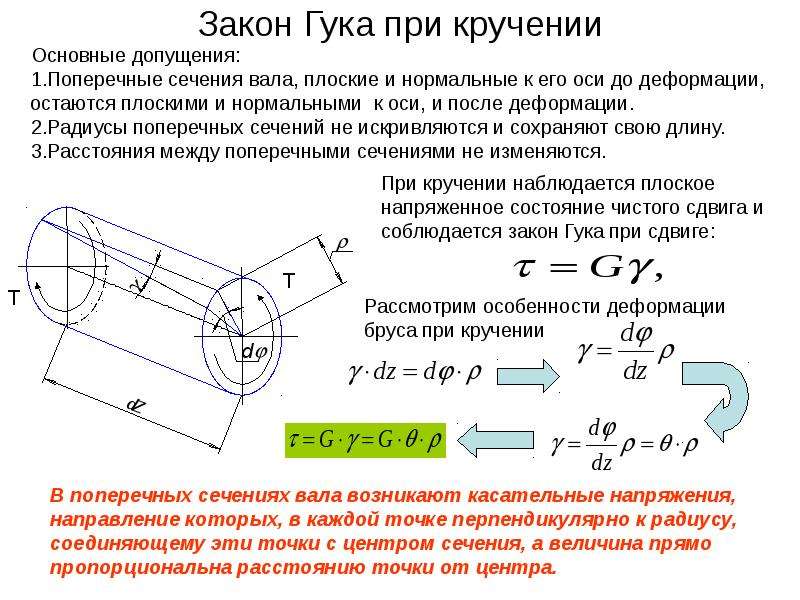
Закон Гука для малых деформаций кручения выражается формулой

M = Gкр.j

где Gкр.– модуль кручения.

Модуль кручения , помимо материала, зависит также от формы и размеров тела.

Представьте, перед вами цилиндр (или проволока). Если вы начнёте его (её) верхний конец поворачивать вдоль оси, закрепив нижний конец, то при повороте верхней грани на один радиан вы прикладываете вращающий момент, в точности равный модулю кручения (рис.1; 2). Это и есть его определение.

Модуль кручения Gкр показывает, какой момент силы нужно приложить, чтобы закрутить проволоку на угол в 1 рад.

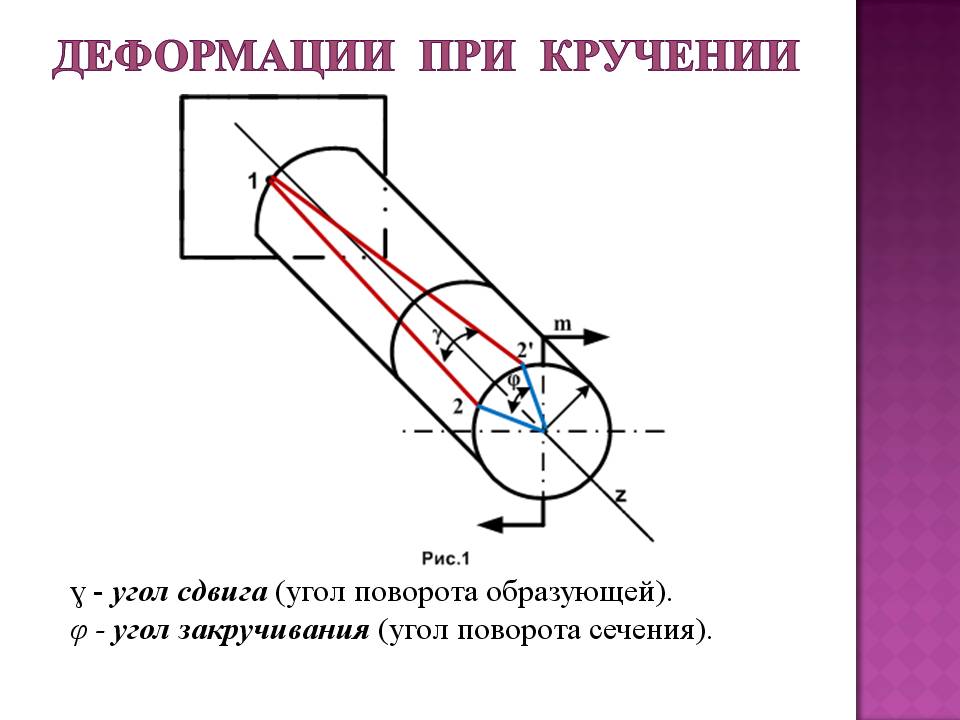
Рис. 2.

Деформация кручения является частным случаем деформации сдвига.

Сдвиг

Сдвигом называют такую деформацию твердого тела, при которой все его плоские слои, параллельные некоторой плоскости сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу (рис. 3).

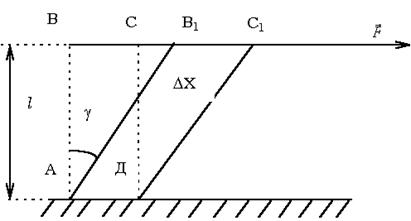
Рис. 3.

Деформация сдвига возникает под действием сил, приложенных к двум противоположным граням тела так, как показано на рисунках 3; 4. Эти силы вызывают смещение слоев тела, параллельных направлению сил. Расстояние между слоями не изменяется. Любой прямоугольный параллелепипед, мысленно выделенный в теле, превращается в наклонный.

Рис. 4.

Мерой деформации сдвига является угол сдвига γ — угол наклона вертикальных граней (рис. 5).

Рис. 5.

Сдвиг происходит под действием касательной силы F, приложенной к грани ВС, параллельной плоскости сдвига. Грань АД, параллельная ВС, закреплена неподвижно.

Так как угол мал, формулу можно записать в виде:

где СС1 = D X — абсолютный сдвиг, γ — угол сдвига, называемый также относительным сдвигом, выражается в радианах.

По закону Гука относительный сдвиг γ пропорционален касательному напряжению τ = F/S, где S — площадь поверхности грани ВС, т.е.

τ = F / S = Gg

где G — модуль сдвига.

Закон Гука для малой деформации сдвига выражается формулой:

Коэффициент G, зависящий от материала тела, называется модулем сдвига и характеризует упругие свойства тела при деформации сдвига. Например, для стального образца G = 76 ГПа.

Модуль сдвига равен касательному напряжению, которое возникло бы в образце при относительном сдвиге, равном 1 (при условии, что закон Гука выполняется).

Деформацию сдвига испытывают, например, заклепки и болты, соединяющие металлические конструкции. Сдвиг при больших углах приводит к разрушению тела — срезу. Срез происходит при работе ножниц, пилы и др.

Обратите внимание на принципиальное отличие модуля кручения от модуля сдвига, который зависит только от материала. Модуль кручения зависит не только от материала, но ещё и от диаметра и от длины цилиндра

Измерения

1. Прежде всего установите диапазон амплитуд, в котором выполняется условие (8). Для этого укрепите грузы на некотором расстоянии от проволоки и возбудите в системе крутильные колебания. Измеряя время нескольких (не менее 10-ти) полных колебаний, найдите период Т1

   . уменьшая амплитуду вдвое, тем же способом найдите соответствующий периодТ2 . еслиТ1= Т2 , то для проведения измерений можно выбрать любую амплитуду не больше первой. Если же окажется, что , то амплитуду необходимо уменьшить до такого значения , начиная с которого для всех < будет справедливо равенствоТ1= Т2 .

2. Проверьте справедливость неравенства (7).
3. Установив грузы так, чтобы их центры масс находились на некотором расстоянии L1

   от оси системы, измерьте период, как описано выше. ЕслиJ – момент инерции без грузов, аJ1 – момент инерции грузов, то, очевидно:

. (9)

Изменив расстояние грузов до величины L2

, аналогично получим:

. (10)

Из (9) и (10) следует:

,

где 2т

– масса двух грузов. Масса одного груза 550 г.

Определение величины ƒ

проведите для нескольких (не менее 5-ти) пар значенийL1 иL2 . величинуƒ можно также найти из наклона прямой в графике, по осям которого отложеныL2 иТ2 . разработка этого вопроса предоставляется читателю.

1. Зная ƒ

   , найдите значение модуля сдвигаG по формуле (2) и оцените допущенную при этом погрешность.

Деформация твёрдого тела: её виды, измерение

Подробности Молекулярно-кинетическая теория Опубликовано 17.11.2014 18:20 10272

Под воздействием внешних сил твёрдые тела меняют свою форму и объем, т.е. деформируются.

В результате действия приложенных к телу сил частицы, из которых оно состоит, перемещаются. Изменяются расстояния между атомами, их взаимное расположение. Это явление называют деформацией.

Если после прекращения действия силы тело возвращает свою первоначальную форму и объём, то такая деформация называется упругой, или обратимой. В этом случае атомы снова занимают положение, в котором они находились до того, как на тело начала действовать сила.

Если мы сожмём резиновый мячик, он изменит форму. Но тут же восстановит её, как только мы его отпустим. Это пример упругой деформации.

Если же в результате действия силы атомы смещаются от положений равновесия на такие расстояния, что межатомные связи на них уже не действуют, они не могут вернуться в первоначальное состояние и занимают новые положения равновесия. В этом случае в физическом теле происходят необратимые изменения.

Сдавим кусочек пластилина. Свою первоначальную форму он не сможет вернуть, когда мы прекратим воздействовать на него. Он деформировался необратимо. Такую деформацию называют пластичной, или необратимой.

Необратимые деформации могут также происходить постепенно с течением времени, если на тело воздействует постоянная нагрузка, или под влиянием различных факторов в нём возникает механическое напряжение. Такие деформации называются деформациями ползучести.

Например, когда детали и узлы каких-то агрегатов во время работы испытывают серьёзные механические нагрузки, а также подвергаются значительному нагреву, в них со временем наблюдается деформация ползучести.

Под воздействием одной и той же силы тело может испытывать упругую деформацию, если сила приложена к нему на короткое время. Но если эта же сила будет воздействовать на это же тело длительно, то деформация может стать необратимой.

Величина механического напряжения, при которой деформация тела всё ещё будет упругой, а само тело восстановит свою форму после снятия нагрузки, называется пределом упругости. При значениях выше этого предела тело начнёт разрушаться. Но разрушить твёрдое тело не так-то просто. Оно сопротивляется. И это его свойство называется прочностью.

Когда два автомобиля, соединённые буксировочным тросом, начинают движение, трос подвергается деформации. Он натягивается, а его длина увеличивается. А когда они останавливаются, натяжение ослабевает, и длина троса восстанавливается. Но если трос недостаточно прочный, он просто разорвётся.

Это интересно: Чем склеить оргстекло намертво в домашних условиях

Деформация кручения

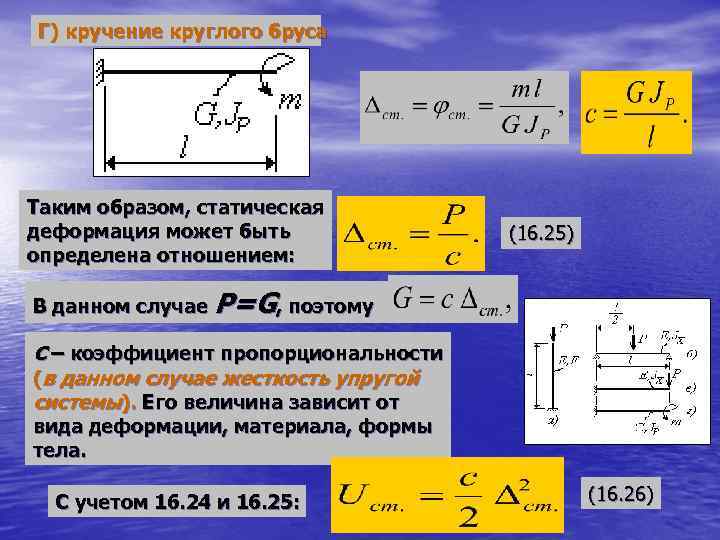
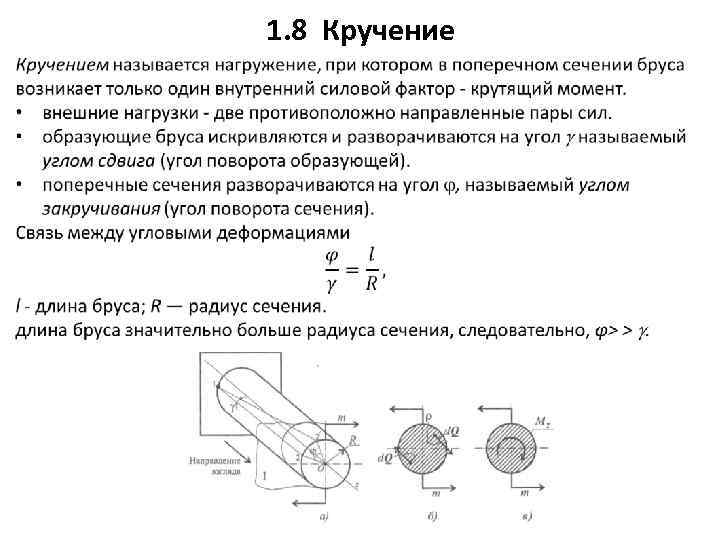
Основные понятия о кручении. Кручение круглого бруса.

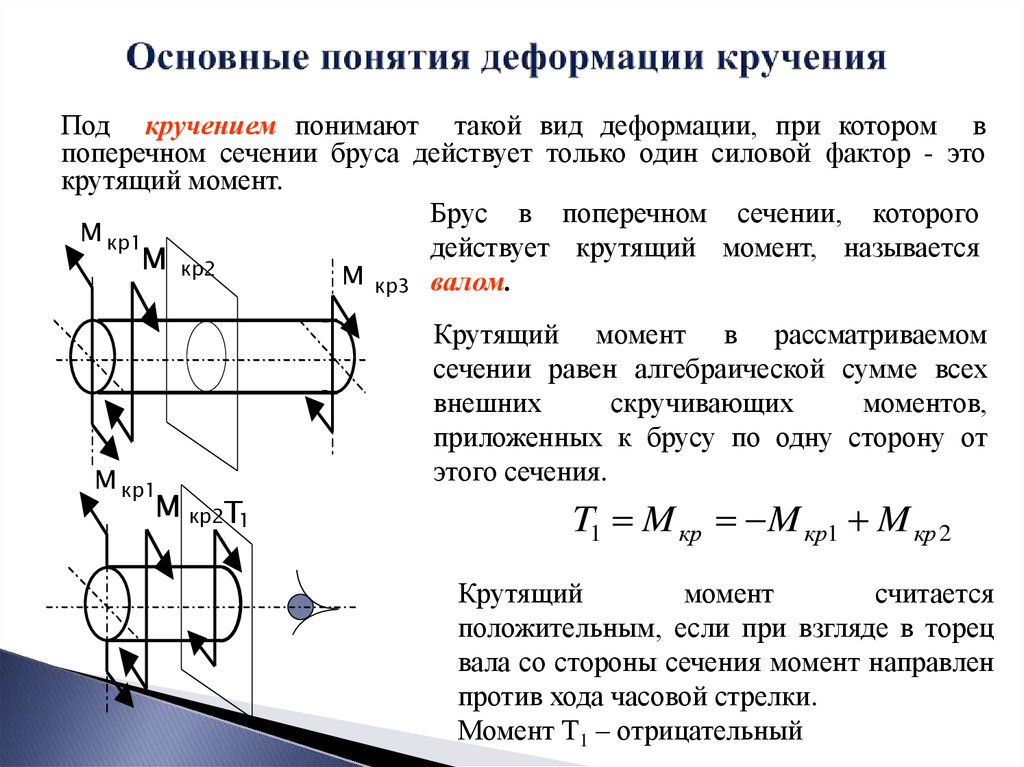
Кручением называют такой вид деформации, при котором в любом поперечном сечении бруса возникает только крутящий момент, т. е. силовой фактор, вызывающий круговое перемещение сечения относительно оси, перпендикулярной этому сечению, либо препятствующий такому перемещению. Другими словами – деформации кручения возникают, если к прямому брусу в плоскостях, перпендикулярных его оси приложить пару или пары сил.
Моменты этих пар сил называют скручивающими или вращающими. Вращающий момент обозначают Т.
Такое определение условно разделяет силовые факторы деформации кручения на внешние (скручивающие, вращающие моменты Т) и внутренние (крутящие моменты М_кр).

В машинах и механизмах кручению наиболее часто подвергаются круглые или трубчатые валы, поэтому расчеты на прочность и жесткость чаще всего производят для таких узлов и деталей.

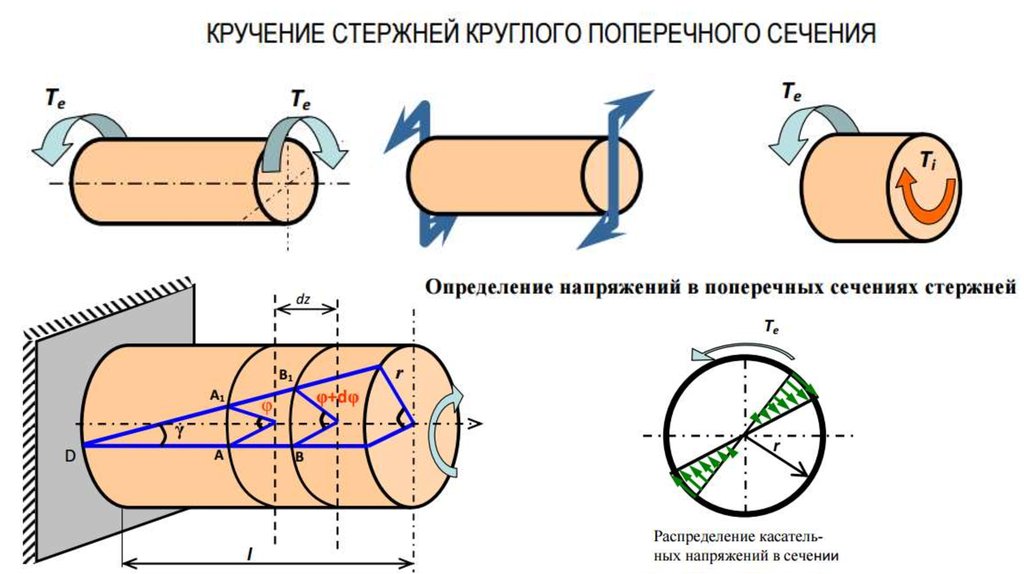
Рассмотрим кручение круглого цилиндрического вала.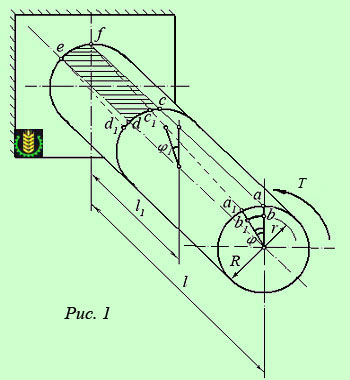
Представьте резиновый цилиндрический вал у которого жестко закреплен один из концов, а на поверхности нанесена сетка из продольных линий и поперечных окружностей. К свободному концу вала приложим пару сил, перпендикулярно оси этого вала, т. е. закрутим его вдоль оси. Если внимательно рассмотреть линии сетки на поверхности вала, то можно заметить, что:
– ось вала, которую называют осью кручения, останется прямолинейной;
– диаметры окружностей останутся такими же, а расстояние между соседними окружностями не изменится;
– продольные линии на валу обратятся в винтовые линии.

Из этого можно заключить, что при кручении круглого цилиндрического бруса (вала) справедлива гипотеза плоских сечений, а также предположить, что радиусы окружностей остаются при деформации прямыми (поскольку их диаметры не изменились). А поскольку в сечениях вала отсутствуют продольные силы, то расстояние между ними сохраняется.

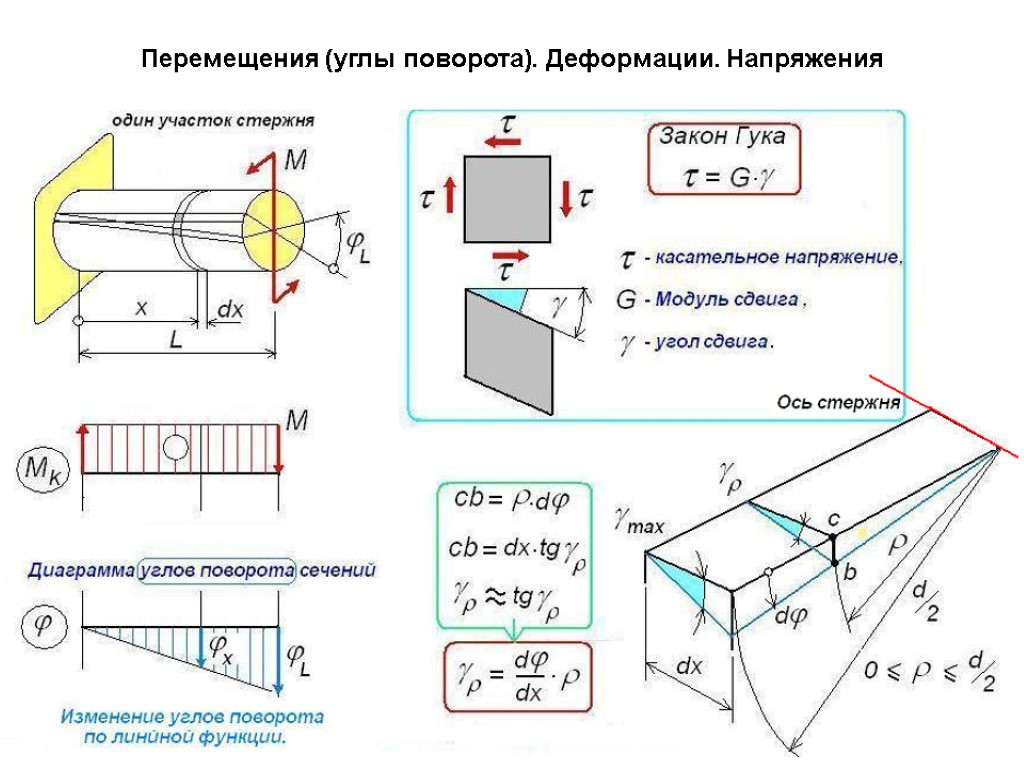
Следовательно, деформация кручения круглого вала заключается в повороте поперечных сечений относительно друг друга вокруг оси кручения, причем углы поворота их прямо пропорциональны расстояниям от закрепленного сечения – чем дальше от закрепленного конца вала находится какое-либо сечение, тем на больший угол относительно оси вала оно закручивается.
Для каждого сечения вала угол поворота равен углу закручивания части вала, заключенного между этим сечением и заделкой (закрепленным концом).



рис. 1φφ₁ l₁lφ = φ₁ / l₁ = φ / l = const

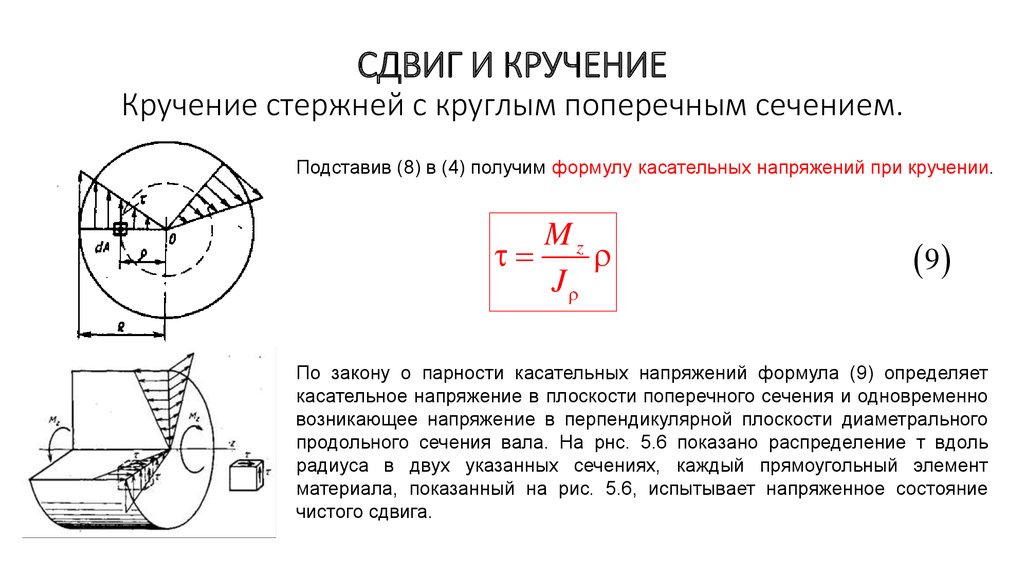
Если мы рассмотрим тонкий слой на поверхности вышеупомянутого резинового цилиндрического бруса (рис. 1), ограниченный ячейкой сетки cdef, то заметим, что эта ячейка при деформации перекашивается, и ее сторона, удаленная от закрепленного сечения, смещается в сторону закручивания бруса, занимая положение c₁d₁ef.

Следует отметить, что аналогичная картина наблюдается при деформации сдвига, только в этом случае поверхность деформируется из-за поступательного перемещения сечений друг относительно друга, а не из-за вращательного перемещения, как при деформации кручения. На основании этого можно сделать вывод, что при кручении в поперечных сечениях возникают только касательные внутренние силы (напряжения), образующие крутящий момент.

Итак, крутящий момент есть результирующий момент относительно оси бруса внутренних касательных сил, действующих в поперечном сечении.

***

Материалы раздела “Деформация кручения”:

• Понятие о кручении цилиндрического бруса (вала)
• Построение эпюр крутящих моментов
• Деформации и напряжения, возникающие при кручении
• Расчеты на прочность и жесткость при кручении
• Расчет цилиндрических винтовых пружин

Учебные дисциплины

• Инженерная графика
• МДК.01.01. «Устройство автомобилей»
•    Карта раздела
•       Общее устройство автомобиля
•       Автомобильный двигатель
•       Трансмиссия автомобиля
•       Рулевое управление
•       Тормозная система
•       Подвеска
•       Колеса
•       Кузов
•       Электрооборудование автомобиля
•       Основы теории автомобиля
•       Основы технической диагностики
• Основы гидравлики и теплотехники
• Метрология и стандартизация
• Сельскохозяйственные машины
• Основы агрономии
• Перевозка опасных грузов
• Материаловедение
• Менеджмент
• Техническая механика
• Советы дипломнику

Олимпиады и тесты

• «Инженерная графика»
• «Техническая механика»
• «Двигатель и его системы»
• «Шасси автомобиля»
• «Электрооборудование автомобиля»

Контрольные вопросы

1. Выведите формулу (2).
2. При определении модуля сдвига статическим способом зависимость рекомендуется снять как при возрастающих, так и при убывающих значениях М

   . Почему? Совпадут ли оба полученные таким образом результаты, если трение в осях блоковБ будет значительным?

3. При определении модуля сдвига динамическим способом указывалось, что период колебаний не зависит от амплитуды только при сравнительно небольших значениях последней. Объясните качественно, как будет меняться период при возрастании амплитуды?
4. Какому методу определения G

   вы отдадите предпочтение на практике, статическому или динамическому?

5. Как при динамическом определении G

   измерить величиныL1 иL2 ? Имеет ли смысл выбирать их малыми?

6. Как оценить ошибку измерений по графику зависимости Т2

   отL2 ?