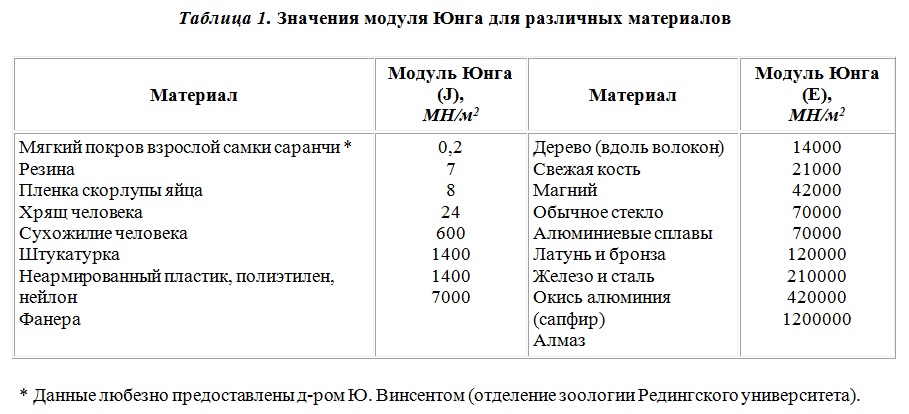
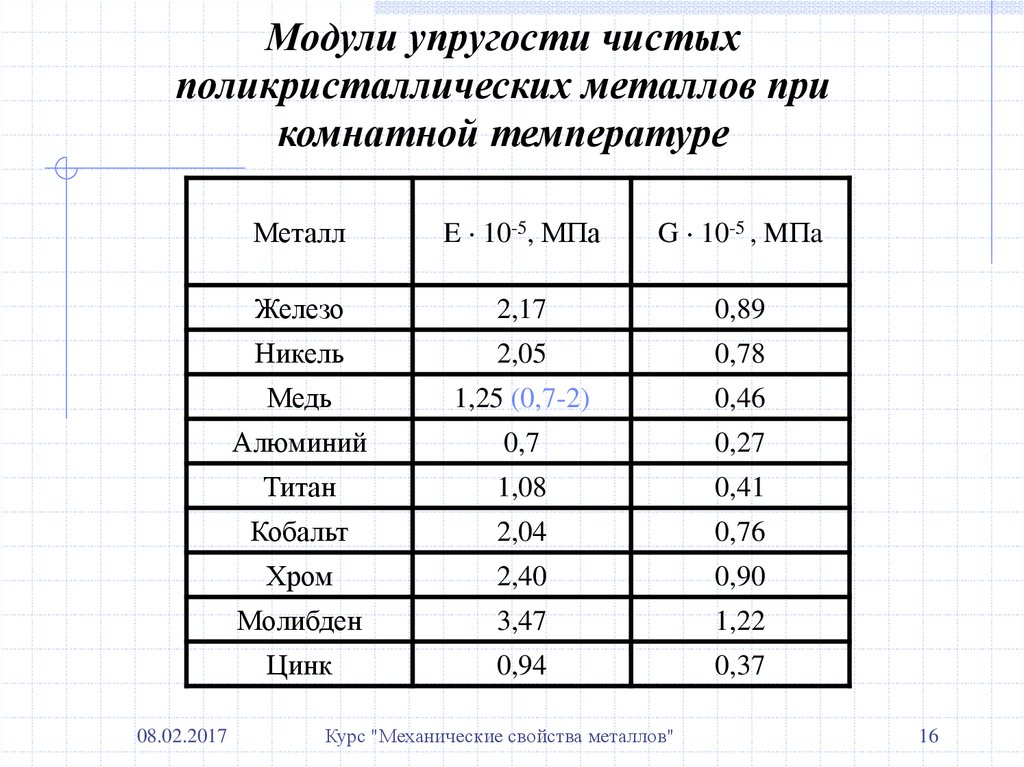
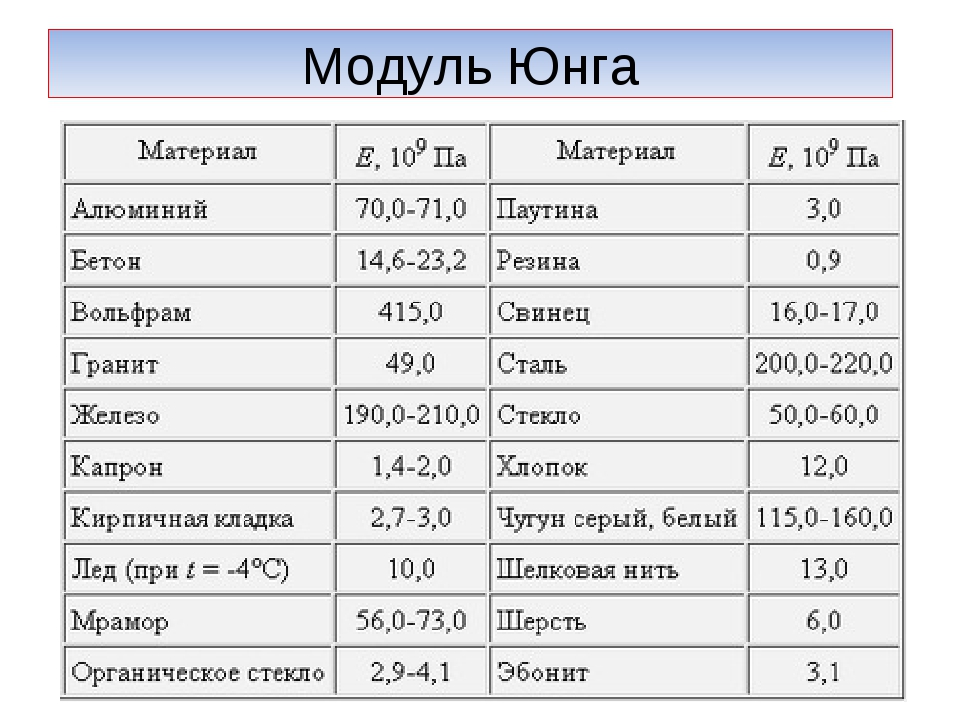
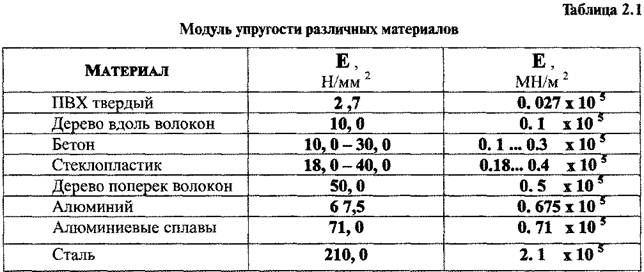
Предел прочности
Твердые тела способны выдерживать ограниченные нагрузки, превышение предела приводит к разрушению структуры металла, формированию заметных сколов или микротрещин. Возникновение дефектов сопряжено со снижением эксплуатационных свойств или полным разрушением. Прочность сплавов и готовых изделий проверяют на испытательных стендах. Стандартами предусмотрен ряд испытаний:
- Продолжительное применение деформирующего усилия;
- Кратковременные и длительные ударные воздействия;
- Растяжение и сжатие;
- Гидравлическое давление и др.
В сложных механизмах и системах выход из строя одного элемента автоматически становится причиной повышения нагрузок на другие. Как правило, разрушения начинаются на тех участках, где напряжения максимальны. Запас прочности служит гарантией безопасности оборудования во внештатных ситуациях и продлевает срок его службы.
Оцените нашу статью
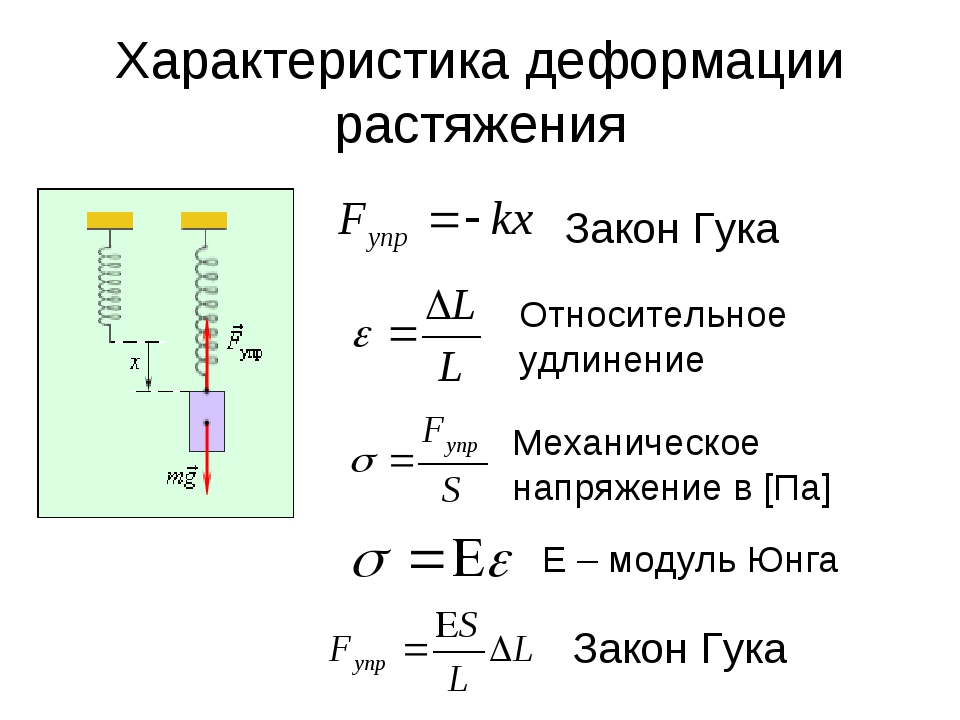
Диаграмма растяжения
Для исследования деформации растяжения стержень из исследуемого материала при помощи специальных устройств (например, с помощью гидравлического пресса) подвергают растяжению и измеряют удлинение образца и возникающее в нем напряжение. По результатам опытов вычерчивают график зависимости напряжения σ
от относительного удлиненияε . Этот график называют диаграммой растяжения (рис. 10).
Рис. 10
Многочисленные опыты показывают, что при малых деформациях напряжение σ
прямо пропорционально относительному удлинениюε (участокОА диаграммы) – выполняется закон Гука.
Эксперимент показывает, что малые деформации полностью исчезают после снятия нагрузки (наблюдается упругая деформация). При малых деформациях выполняется закон Гука. Максимальное напряжение, при котором еще выполняется закон Гука, называется пределом пропорциональности
σп . Он соответствует точки А диаграммы.
Если продолжать увеличивать нагрузку при растяжении и превзойти предел пропорциональности, то деформация становится нелинейной (линия ABCDEK
). Тем не менее при небольших нелинейных деформациях после снятия нагрузки форма и размеры тела практически восстанавливаются (участокАВ графика).Максимальное напряжение, при котором еще не возникают заметные остаточные деформации, называется пределом упругостиσуп . Он соответствует точке В диаграммы. Предел упругости превышает предел пропорциональности не более чем на 0,33%. В большинстве случаев их можно считать равными.
Если внешняя нагрузка такова, что в теле возникают напряжения, превышающие предел упругости, то характер деформации меняется (участок BCDEK
). После снятия нагрузки образец не принимает прежние размеры, а остается деформированным, хотя и с меньшим удлинением, чем при нагрузке (пластическая деформация).
За пределом упругости при некотором значении напряжения, соответствующем точке С
диаграммы, удлинение возрастает практически без увеличения нагрузки (участокCD диаграммы почти горизонтален). Это явление называетсятекучестью материала .
При дальнейшем увеличении нагрузки напряжение повышается (от точки D
), после чего в наименее прочной части образца появляется сужение («шейка»). Из-за уменьшения площади сечения (точкаЕ ) для дальнейшего удлинения нужно меньшее напряжение, но, в конце концов, наступает разрушение образца (точкаК ).Наибольшее напряжение, которое выдерживает образец без разрушения, называется пределом прочности . Обозначим егоσ пч (оно соответствует точкеЕ диаграммы). Его значение сильно зависит от природы материала и его обработки.
Чтобы свести к минимуму возможность разрушения сооружения, инженер должен при расчетах допускать в его элементах такие напряжения, которые будут составлять лишь часть предела прочности материала. Их называют допустимыми напряжениями. Число, показывающее, во сколько раз предел прочности больше допустимого напряжения, называют коэффициентом запаса прочности
. Обозначив запас прочности через n, получим: \(~n = \frac{\sigma_{np}}{\sigma}\) .
Запас прочности выбирается в зависимости от многих причин: качества материала, характера нагрузки (статическая или изменяющаяся со временем), степени опасности, возникающей при разрушении, и т.д. На практике запас прочности колеблется от 1,7 до 10. Выбрав правильно запас прочности, инженер может определить допустимое в конструкции напряжение.
Что это такое?
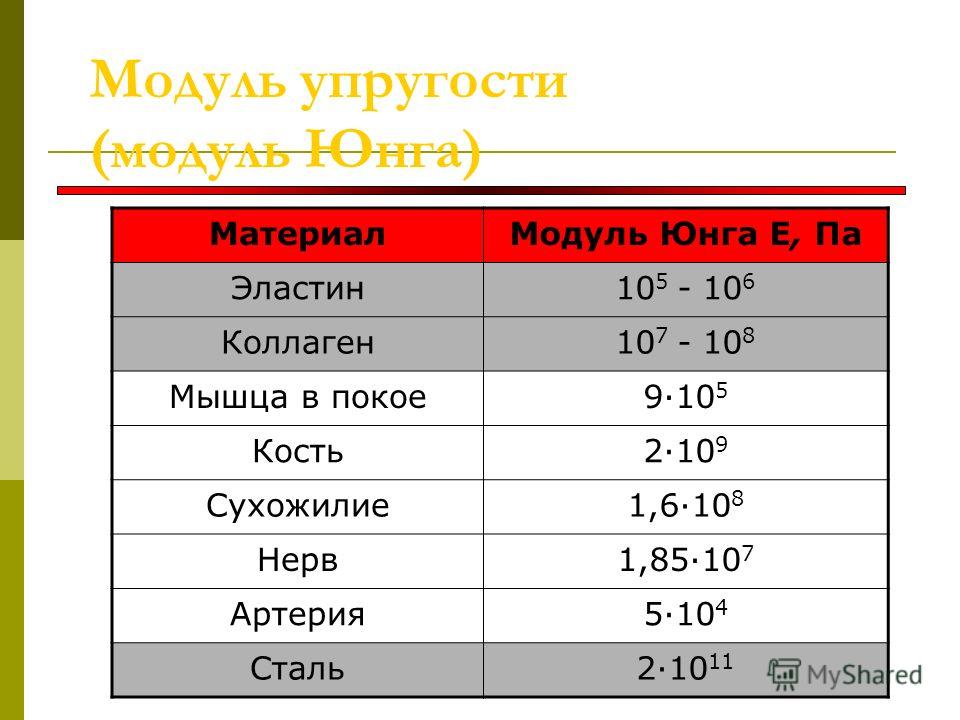
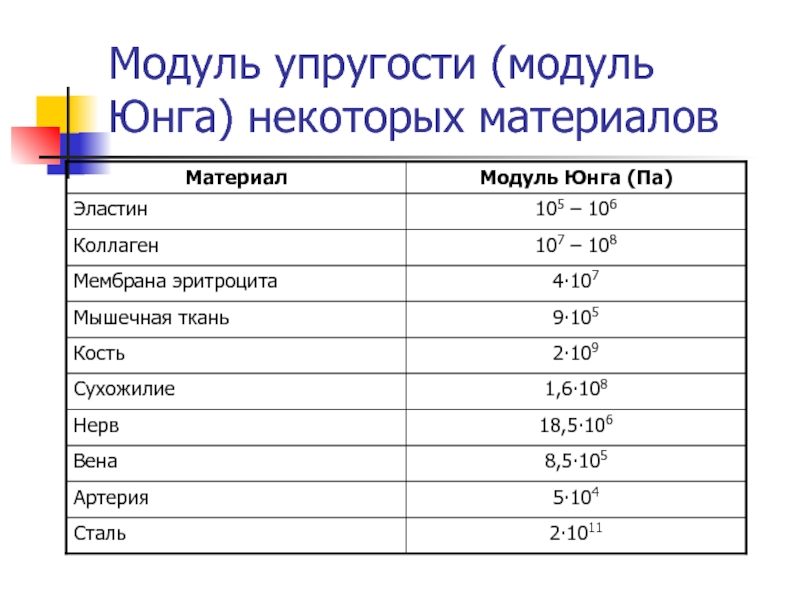
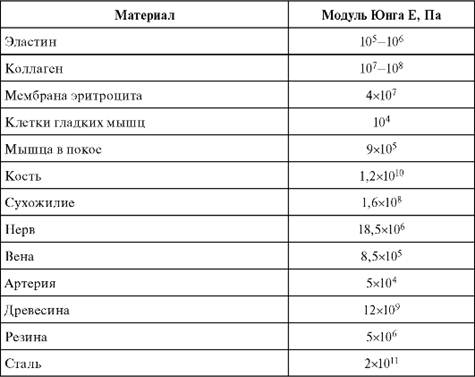
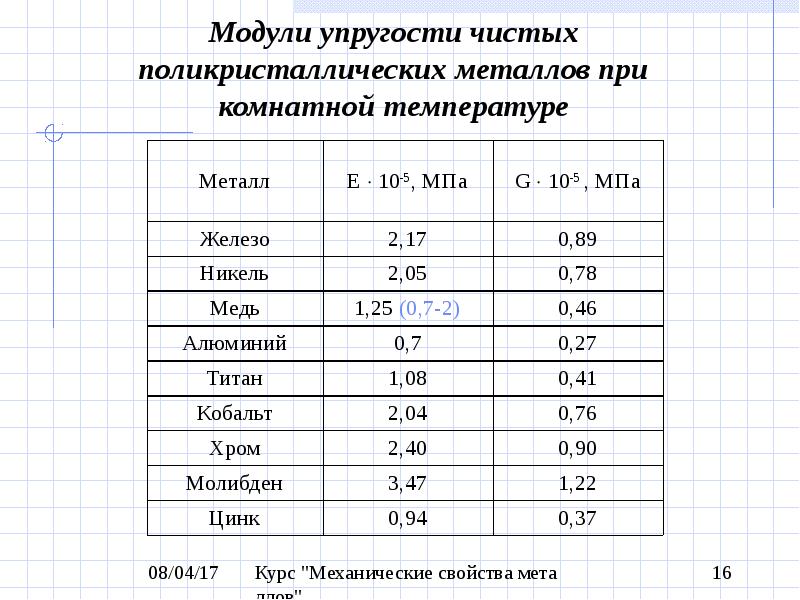
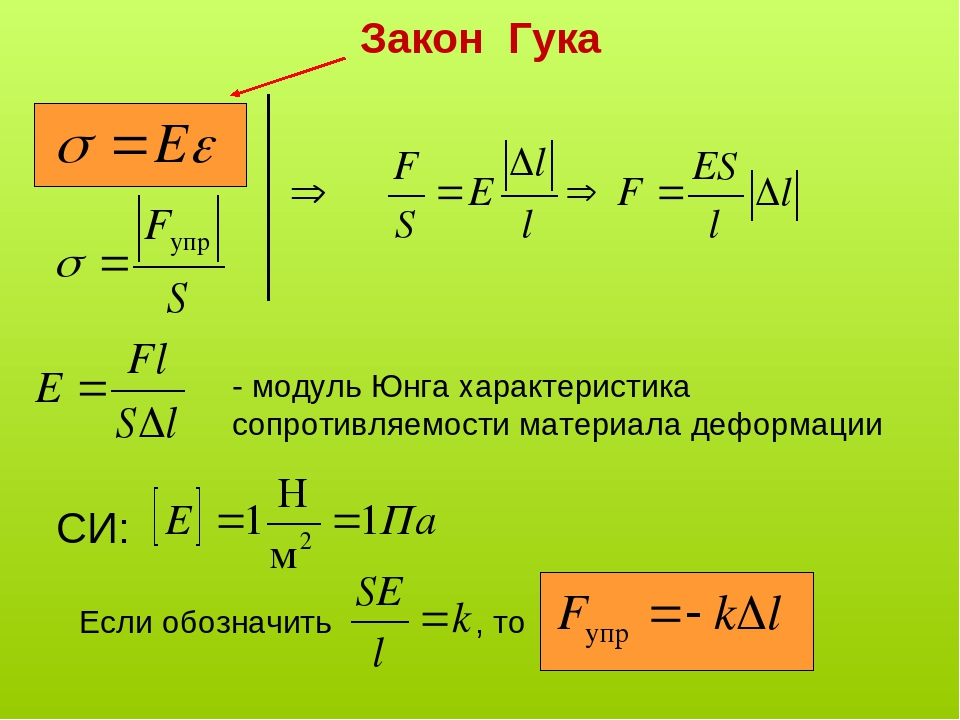
Модуль упругости (модуль Юнга) – показатель, определяющий механическую реакцию материала. При помощи данного параметра удается охарактеризовать поведение образца при растяжении. Если говорить более простым языком, то модуль упругости означает пластичные свойства стали, и чем выше показатель, тем меньше растяжение. В теории модуль Юнга обозначают буквой «Е». Это один из компонентов закона Гука, в котором рассматриваются возможные деформации упругих тел. Посредством данной величины удается связать возникающие в материале напряжения с деформацией, которую он испытывает. Единица измерения модуля упругости – паскали (Па) или мегапаскали (МПа). Однако часто инженеры при проведении расчетов отдают предпочтение кгс/см2. Показатель определяют путем исследований в лабораториях, фиксируя образцы на специальном оборудовании. В основе методики лежит разрыв образцов в форме гантелей на автоматизированных установках.
В ходе эксперимента автоматика отслеживает показатели изменения длины и натяжения заготовки, при которых она разрушается, а затем делит результаты. Полученное число и будет модулем Юнга или модулем упругости. Примечательно, что подобная методика определения показателя используется для определения Е:
- стали;
- меди;
- других упругих образцов.


В хрупких материалах параметр определяют путем сжатия до момента появления трещин. Стоит подробнее остановиться на разборе модуля Юнга с точки зрения физики. В процессе принудительного нагружения, которое приводит к изменению формы материала, внутри него возникают ответные усилия. Силы начинают оказывать сопротивление напряжениям извне и стремятся вернуть форму тела. Если образец совершенно не реагирует на нагрузку (точнее, полностью меняет форму и не восстанавливает ее при снятии усилий), его принято считать пластичным. В качестве примера стоит назвать пластилин, который наглядно отражает теорию на практике. Исследованием упругости материалов занимался ученый Р. Гук, которого интересовало, как будут меняться и удлиняться стержни разных материалов под воздействием гирь. Благодаря ранее проведенной серии опытов удалось доказать, что величины абсолютного удлинения и исходной длины прямо пропорциональны. В то же время абсолютное удлинение обратно пропорционально площади поперечного сечения исследуемого стержня.


Гук вывел целый закон, а также ввел параметр Е для характеристики свойств упругого материала. Таким образом, физический смысл модуля заключается в том, что параметр соответствует напряжению, вызываемому в стержне при растягивании на длину, которая в два раза выше при условии отсутствия видимых разрушений образца.
Посредством модуля Е удается предугадать, как будет вести себя материал при определенных нагружениях. Однако он не дает понимания того, что с ним произойдет при других способах нагружения. Поэтому для проведения эффективных расчетов необходимо введение дополнительных параметров.
- Жесткость. Показатель демонстрирует степень пластичности узла исследуемого образца. Единица измерения параметра – кгс.
- Относительное удлинение в продольном направлении. При расчете используются два показателя: величина абсолютного удлинения и общая длина образца. Показатель не имеет единицы измерения, однако для упрощенного понимания его умножают на 100%.
- Относительное удлинение в поперечном направлении. Высчитывается таким же образом, как и предыдущий параметр, только вместо длины используют диаметр стержня-образца. Как показали испытания, поперечное удлинение обычно меньше продольного.
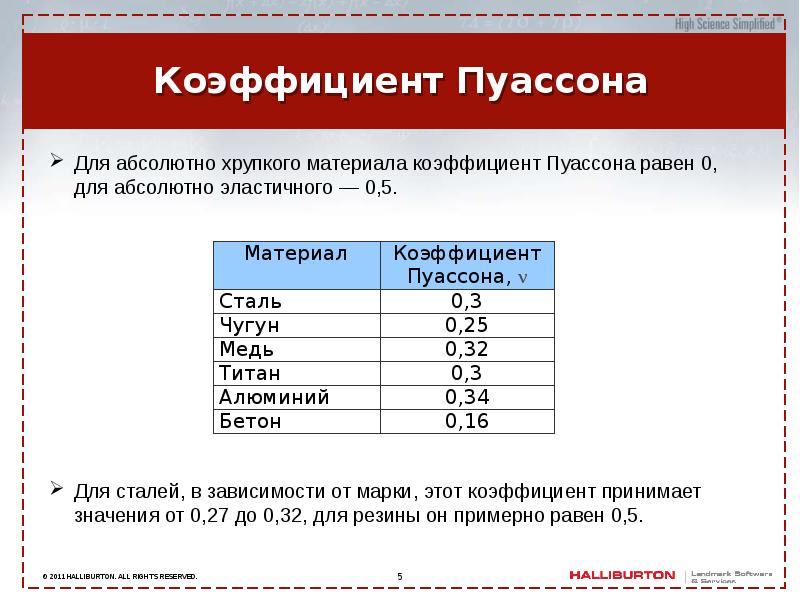
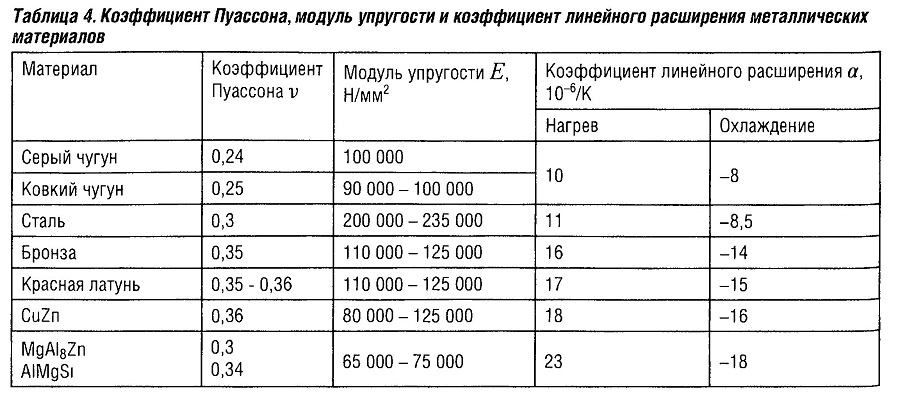
- Коэффициент Пуассона. Представляет собой соотношение двух последних показателей. Параметр делает возможным описание того, как материал будет менять свою форму, опираясь на величину нагрузки и место ее приложения.
- Модуль сдвига. С его помощью удается описать поведение материала с упругими свойствами при воздействии сил по касательной. Другими словами, помогает оценить работу конструкции при воздействии на нее ветра под углом в 90 градусов.


Допускаемое механическое напряжение в некоторых материалах при растяжении
Из жизненного опыта известно, что разные материалы по-разному сопротивляются изменению формы. Прочностные характеристики кристаллических и других твердых тел определяются силами межатомного взаимодействия. По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу. Эти силы достигают максимума при определенной величине напряжения, равной приблизительно одной десятой от модуля Юнга.
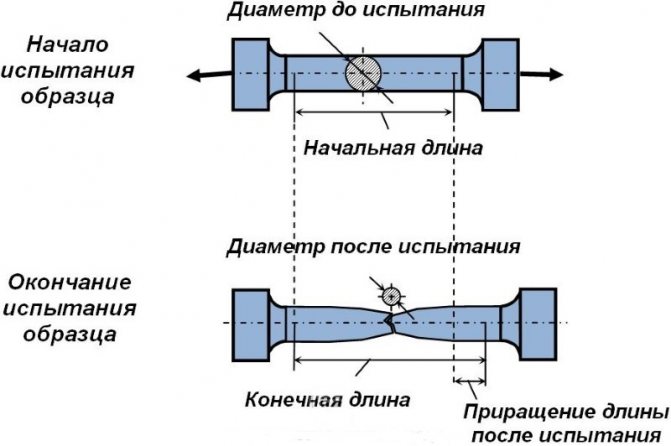
Испытание на растяжение
Эту величину называют теоретической прочностью, при ее превышении начинается разрушение материала. В реальности разрушение начинается при меньших значениях, поскольку строение реальных образцов неоднородно. Это вызывает неравномерное распределение напряжений, и разрушение начинается с тех участков, где напряжения максимальны.
Значения σраст в МПа:
| Материалы | σраст | |
| Бор | 5700 | 0,083 |
| Графит | 2390 | 0,023 |
| Сапфир | 1495 | 0,030 |
| Стальная проволока | 415 | 0,01 |
| Стекловолокно | 350 | 0,034 |
| Конструкционная сталь | 60 | 0,003 |
| Нейлон | 48 | 0,0025 |
Эти цифры учитываются конструкторами при выборе материала деталей будущего изделия. С их использованием также проводятся прочностные расчеты. Так, например, тросы, используемые для подъемно- транспортных работ, должны иметь десятикратный запас по прочности. Периодически их проверяют, подвешивая груз в десять раз больше, чем паспортная грузоподъемность троса.
Запасы прочности, закладываемые в ответственные конструкции, также многократны.
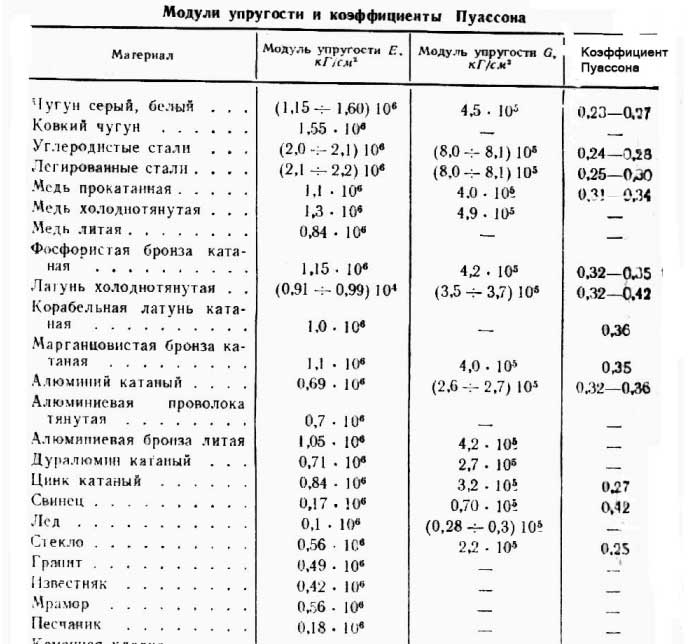
Модуль упругости Юнга и сдвига, коэффициент Пуассона значения (Таблица)
Упругие свойства тел
Ниже приводятся справочные таблицы общеупотребительных констант; если известны две их них, то этого вполне достаточно для определения упругих свойств однородного изотропного твердого тела.
Модуль Юнга или модуль продольной упругости в дин/см2.
Модуль сдвига или модуль кручения G в дин/см2.
Модуль всестороннего сжатия или модуль объемной упругости К в дин/см2.
Объем сжимаемости k=1/K/.
Коэффициент Пуассона µ равен отношению поперечного относительного сжатия к продольному относительному растяжению.
Для однородного изотропного твердого материала имеют место следующие соотношения между этими константами:
G = E / 2(1 + μ) — (α)
μ = (E / 2G) — 1 — (b)
K = E / 3(1 — 2μ) — (c)
Коэффициент Пуассона имеет положительный знак, и его значение обычно заключено в пределах от 0,25 до 0,5, но в некоторых случаях он может выходить за указанные пределы. Степень совпадения наблюдаемых значений µ и вычисленных по формуле (b) является показателем изотропности материала.
Таблицы значений Модуля упругости Юнга, Модуля сдвига и коэффициента Пуассона
Курсивом даны значения, вычисленные из соотношений (a), (b), (c).
| Материал при 18°С | Модуль Юнга E, 1011 дин/см2. | Модуль сдвига G, 1011 дин/см2. | Коэффициент Пуассона µ | Модуль объемной упругости К, 1011 дин/см2. |
| Алюминий | 7,05 | 2,62 | 0,345 | 7,58 |
| Висмут | 3,19 | 1,20 | 0,330 | 3,13 |
| Железо | 21,2 | 8,2 | 0,29 | 16,9 |
| Золото | 7,8 | 2,7 | 0,44 | 21,7 |
| Кадмий | 4,99 | 1,92 | 0,300 | 4,16 |
| Медь | 12,98 | 4,833 | 0,343 | 13,76 |
| Никель | 20,4 | 7,9 | 0,280 | 16,1 |
| Платина | 16,8 | 6,1 | 0,377 | 22,8 |
| Свинец | 1,62 | 0,562 | 0,441 | 4,6 |
| Серебро | 8,27 | 3,03 | 0,367 | 10,4 |
| Титан | 11,6 | 4,38 | 0,32 | 10,7 |
| Цинк | 9,0 | 3,6 | 0,25 | 6,0 |
| Сталь (1% С) 1) | 21,0 | 8,10 | 0,293 | 16,88 |
| (мягкая) | 21,0 | 8,12 | 0,291 | 16,78 |
| Константан 2) | 16,3 | 6,11 | 0,327 | 15,7 |
| Манганин | 12,4 | 4,65 | 0,334 | 12,4 |
| 1) Для стали, содержащий около 1% С, упругие константы, как известно , меняются при термообработке. 2) 60% Cu, 40% Ni. |
Экспериментальные результаты, приводимые ниже, относятся к обычным лабораторным материалам, главным образом проволокам.
| Вещество | Модуль Юнга E, 1011 дин/см2. | Модуль сдвига G, 1011 дин/см2. | Коэффициент Пуассона µ | Модуль объемной упругости К, 1011 дин/см2. |
| Бронза (66% Cu) | -9,7-10,2 | 3,3-3,7 | 0,34-0,40 | 11,2 |
| Медь | 10,5-13,0 | 3,5-4,9 | 0,34 | 13,8 |
| Нейзильбер1) | 11,6 | 4,3-4,7 | 0,37 | — |
| Стекло | 5,1-7,1 | 3,1 | 0,17-0,32 | 3,75 |
| Стекло иенское крон | 6,5-7,8 | 2,6-3,2 | 0,20-0,27 | 4,0-5,9 |
| Стекло иенское флинт | 5,0-6,0 | 2,0-2,5 | 0,22-0,26 | 3,6-3,8 |
| Железо сварочное | 19-20 | 7,7-8,3 | 0,29 | 16,9 |
| Чугун | 10-13 | 3,5-5,3 | 0,23-0,31 | 9,6 |
| Магний | 4,25 | 1,63 | 0,30 | — |
| Бронза фосфористая2) | 12,0 | 4,36 | 0,38 | — |
| Платиноид3) | 13,6 | 3,6 | 0,37 | — |
| Кварцевые нити (плав.) | 7,3 | 3,1 | 0,17 | 3,7 |
| Резина мягкая вулканизированная | 0,00015-0,0005 | 0,00005-0,00015 | 0,46-0,49 | — |
| Сталь | 20-21 | 7,9-8,9 | 0,25-0,33 | 16,8 |
| Цинк | 8,7 | 3,8 | 0,21 | — |
| 1) 60% Cu, 15% Ni, 25% Zn 2) 92,5% Cu, 7% Sn, 0,5% P 3) Нейзильбер с небольшим количеством вольфрама. |
| Вещество | Модуль Юнга E, 1011 дин/см2. | Вещество | Модуль Юнга E, 1011 дин/см2. |
| Цинк (чистый) | 9,0 | Дуб | 1,3 |
| Иридий | 52,0 | Сосна | 0,9 |
| Родий | 29,0 | Красное дерево | 0,88 |
| Тантал | 18,6 | Цирконий | 7,4 |
| Инвар | 17,6 | Титан | 10,5-11,0 |
| Сплав 90% Pt, 10% Ir | 21,0 | Кальций | 2,0-2,5 |
| Дюралюминий | 7,1 | Свинец | 0,7-1,6 |
| Шелковые нити1 | 0,65 | Тиковое дерево | 1,66 |
| Паутина2 | 0,3 | Серебро | 7,1-8,3 |
| Кетгут | 0,32 | Пластмассы: | |
| Лед (-20С) | 0,28 | Термопластичные | 0,14-0,28 |
| Кварц | 7,3 | Термореактивные | 0,35-1,1 |
| Мрамор | 3,0-4,0 | Вольфрам | 41,1 |
| 1) Быстро уменьшается с увеличением нагрузки 2) Обнаруживает заметную упругую усталость |
| Температурный коэффициент (при 150С) Et=E11 (1-ɑ (t-15)), Gt=G11 (1-ɑ (t-15)) | Сжимаемость k, бар-1 (при 7-110С) | |||
| ɑ, для Е | ɑ, для G | |||
| Алюминий | 4,8*10-4 | 5,2*10-4 | Алюминий | 1,36*10-6 |
| Латунь | 3,7*10-4 | 4,6*10-4 | Медь | 0,73*10-6 |
| Золото | 4,8*10-4 | 3,3*10-4 | Золото | 0,61*10-6 |
| Железо | 2,3*10-4 | 2,8*10-4 | Свинец | 2,1*10-6 |
| Сталь | 2,4*10-4 | 2,6*10-4 | Магний | 2,8*10-6 |
| Платина | 0,98*10-4 | 1,0*10-4 | Платина | 0,36*10-6 |
| Серебро | 7,5*10-4 | 4,5*10-4 | Стекло флинт | 3,0*10-6 |
| Олово | — | 5,9*10-4 | Стекло немецкое | 2,57*10-6 |
| Медь | 3,0*10-4 | 3,1*10-4 | Сталь | 0,59*10-6 |
| Нейзильбер | — | 6,5*10-4 | ||
| Фосфористая бронза | — | 3,0*10-4 | ||
| Кварцевые нити | -1,5*10-4 | -1,1*10-4 |
Способы расчета модуля упругости
Известны также и другие характеристики упругости, которые описывают сопротивление материалов к воздействиям как к линейным, так и отличным от них.
Обозначается как Е и выражается в Па или ГПа.
Показывает зависимость относительного удлинения от нормальной составляющей cилы (F) к ее площади распространения (S) и упругости (Е):
σz = F/ES (3)
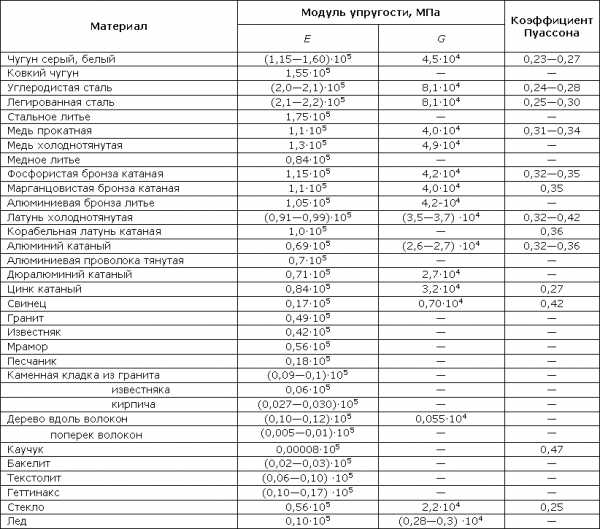
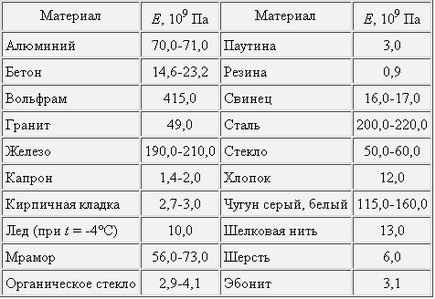
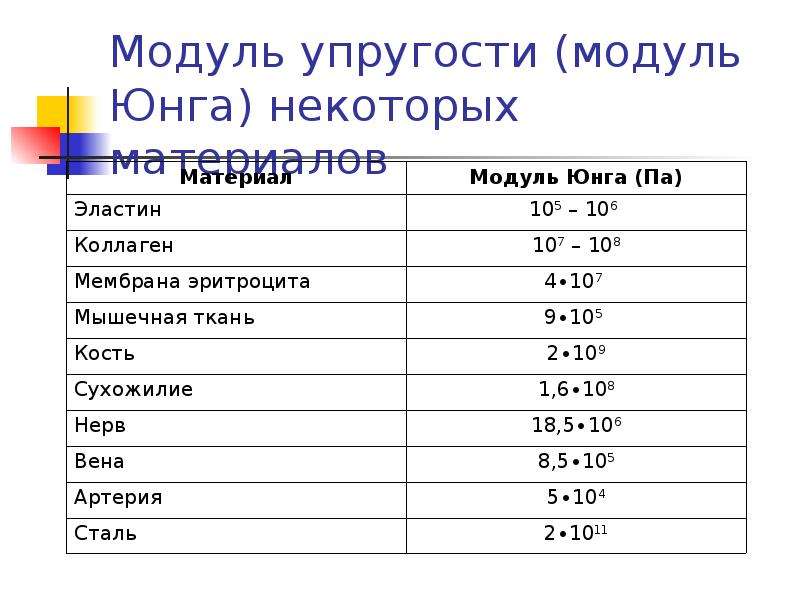
Параметр также называют модулем Юнга или модулем упругости первого рода, в таблице показаны величины для материалов различной природы.
| Название материала | Значение параметра, ГПа |
| Алюминий | 70 |
| Дюралюминий | 74 |
| Железо | 180 |
| Латунь | 95 |
| Медь | 110 |
| Никель | 210 |
| Олово | 35 |
| Свинец | 18 |
| Серебро | 80 |
| Серый чугун | 110 |
| Сталь | 190/210 |
| Стекло | 70 |
| Титан | 112 |
| Хром | 300 |
Модулем упругости второго рода называют модуль сдвига (G), который показывает сопротивление материала к сдвигающей силе (FG). Может быть выражена двумя способами.
Через касательные напряжения (τz) и угол сдвига (γ):
G = τz/γ (4)
Через соотношение модуля упругости первого рода и коэффициента Пуасонна (ν):
G = E/2(1+υ) (5)
Определенное в результате экспериментов значение сопротивления материала изгибу, называется модулем упругости при изгибе, и вычисляется следующим образом:
EИ = ((0,05-0,1)Fр— 0,2Fр)L2 / 4bh3(ƒ2-ƒ1) (6)
где Fр – разрушающая сила, Н;
L – расстояние между опорами, мм;
b, h – ширина и толщина образца, мм;
ƒ1, ƒ2– прогибы, образованные в результате нагрузки F1 и F2.
При равномерном давлении по всему объему на объект, возникает его сопротивление, называемое объемным модулем упругости или модулем сжатия (К). Выразить этот параметр можно, практически через все известные модули и коэффициент Пуассона.

Определение модуля упругости щебеночного основания
Параметры Ламе также используют для описания оценки прочности материала. Их два μ – модуль сдвига и λ. Они помогают учитывать все изменения внутри материала в трехмерном пространстве, тогда соотношения между нормальным напряжением и деформацией будет выглядеть следующим образом:
σ = 2με + λtrace(ε)I (7)
Оба параметра могут быть выражены из следующих соотношений:
λ = νE / (1+ν)(1-2ν) (8)
μ = E / 2(1+ν) (9)
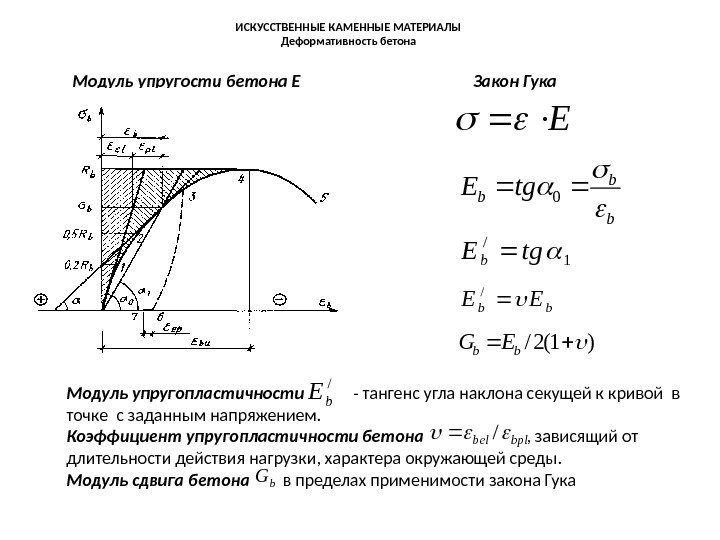
От чего зависит модуль упругости бетона?
Упругие свойства бетона зависят от факторов:
- качества и объемного содержания заполнителей;
- класса материала;
- температуры воздуха и интенсивности радиоактивного излучения;
- влажности среды;
- времени воздействия нагрузки;
- условий твердения смеси;
- возраста бетона;
- армирования.
Заполнители
Бетон представляет собой конгломерат из двух составляющих — цементного камня и заполнителей. В неоднородной структуре возникает сложное напряженное состояние. Более жесткие частицы воспринимают основную часть нагрузки, а вокруг пор и пустот образуются участки с поперечными растягивающими усилиями.
Крупный заполнитель, обладая высоким модулем Юнга, увеличивает упругие свойства бетона. Мелкие пылеватые частицы, поры и пустоты снижают их.
Класс бетона
Чем выше класс материала, т.е. больше его прочность на сжатие и плотность, тем лучше он сопротивляется деформирующим нагрузкам. Наиболее высоким модулем упругости обладает бетон В60 — 39,5 МПа*10-3, минимальный показатель у композита класса В10- 19 МПа*10-3.
Температура и радиация
Повышение температуры окружающей среды, интенсивности солнечной радиации приводят к уменьшению упругих свойств и росту деформаций. Связано это с увеличением внутренней энергии бетона, изменению траекторий движения молекул в твердом теле, линейному расширению материала, и, как следствию, усилению пластичности.
Разницу не учитывают при колебаниях в пределах 20°С. Большие температурные изменения существенно влияют на деформацию бетонных конструкций. В таблице СП 63.13330.2012 указаны величины модулей упругости в зависимости от температуры.
Влажность
Колебания влажности воздуха приводят к изменению упругих свойств материала. В расчетах применяют коэффициент ползучести φ. Чем больше содержание водяных паров в окружающей среде, тем ниже показатель и соответственно меньше пластические деформации конструкции.
Время приложения нагрузки
Модуль упругости зависит от времени действия нагрузки. При мгновенном нагружении конструкции деформации пропорциональны величине внешних сил. При длительных напряжениях величина E уменьшается, изменения развиваются по нелинейной зависимости и суммируются из упругих и пластичных деформаций.
Условия набора прочности
При проведении испытаний замечено, что у бетона естественного твердения модуль упругости выше, чем при обработке материала пропариванием при атмосферном давлении или в автоклавных установках.
Это объясняется тем, что изменение условий набора прочности приводит к образованию большего количества пор и пустот из-за неравномерного температурного расширения объема, ухудшения качества гидратации цементных зерен. Такой бетон обладает более низкими упругими свойствами по сравнению с затвердевшим в нормальных условиях.
Возраст бетона
Свежеуложенный бетон набирает прочность в течение 28 суток. Но даже по истечении этого времени материал при нагрузке обладает одновременно упругими и пластическими свойствами. Наибольшей твердости он достигает примерно через 200-250 суток. Показатель E в этом возрасте максимальный, соответствующий марочной прочности.
Армирование конструкций
Для восприятия растягивающих и сжимающих усилий в железобетон помещают каркасы или сетки из арматуры классов АI, AIII, А500С, Ат800, а также из композитов или древесины.
Применение армирования увеличивает упругость, прочность конструкции на сжатие и на растяжение при изгибе, препятствует образованию усадочных и деформационных трещин.
Расчет жесткости системы
Встречаются более сложные задачи, в которых необходим расчет общей жесткости. В таких заданиях пружины соединены последовательно или параллельно.
Последовательное соединение системы пружин
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
1/k = 1/k1 + 1/k2 + … + 1/ki,
где k — общая жесткость системы, k1, k2, …, ki — отдельные жесткости каждого элемента, i — общее количество всех пружин, задействованных в системе.

Параллельное соединение системы пружин
В случае когда пружины соединены параллельно, величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
k = k1 + k2 + … + ki.
Измерение жесткости пружины опытным путем — в этом видео.
https://youtube.com/watch?v=YjfWehCZnf8
Общее понятие
Модуль упругости (также известный как модуль Юнга) – один из показателей механических свойств материала, который характеризует его сопротивляемость деформации растяжения. Другими словами, его значение показывает пластичность материала. Чем больше модуль упругости, тем менее будет растягиваться какой-либо стержень при прочих равных условиях (величина нагрузки, площадь сечения и прочее).
В теории упругости модуль Юнга обозначается буквой Е. Является составной частью закона Гука (закона о деформации упругих тел). Связывает напряжение, возникающее в материале, и его деформацию.
Согласно международной стандартной системе единиц измеряется в МПа. Но на практике инженеры предпочитают использовать размерность кгс/см2.
Определение модуля упругости осуществляется опытным путем в научных лабораториях. Суть данного способа заключается в разрыве на специальном оборудовании гантелеобразных образцов материала. Узнав напряжение и удлинение, при котором произошло разрушение образца, делят данные переменные друг на друга, тем самым получая модуль Юнга.
Отметим сразу, что таким методом определяются модули упругости пластичных материалов: сталь, медь и прочее. Хрупкие материалы – чугун, бетон – сжимают до появления трещин.
Дополнительные характеристики механических свойств
Модуль упругости дает возможность предугадать поведение материла только при работе на сжатие или растяжение. При наличии таких видов нагрузок как смятие, срез, изгиб и прочее потребуется введение дополнительных параметров:
- Жесткость есть произведение модуля упругости на площадь поперечного сечения профиля. По величине жесткости можно судить о пластичности уже не материала, а узла конструкции в целом. Измеряется в килограммах силы.
- Относительное продольное удлинение показывает отношение абсолютного удлинения образца к общей длине образца. Например, к стержню длиной 100 мм приложили определенную силу. Как результат, он уменьшился в размере на 5 мм. Деля его удлинение (5 мм) на первоначальную длину (100 мм) получаем относительное удлинение 0,05. Переменная является безразмерной величиной. В некоторых случаях для удобства восприятия переводится в проценты.
- Относительное поперечное удлинение рассчитывается аналогично вышепредставленному пункту, но вместо длины здесь рассматривается диаметр стержня. Опыты показывают, что для большинства материалов поперечное удлинение в 3-4 раза меньше, чем продольное.
- Коэффициент Пуансона есть отношение относительной продольной деформации к относительной поперечной деформации. Данный параметр позволяет полностью описать изменение формы под воздействием нагрузки.
- Модуль сдвига характеризует упругие свойства при воздействии на образец касательных напряжений, т. е. в случае, когда вектор силы направлен под 90 градусов к поверхности тела. Примерами таких нагрузок является работа заклепок на срез, гвоздей на смятие и прочее. По большому счету, модуль сдвига связан с таким понятием как вязкость материла.
- Модуль объемной упругости характеризуется изменением объема материала для равномерного разностороннего приложения нагрузки. Является отношением объемного давления к объемной деформации сжатия. Примером такой работы служит опущенный в воду образец, на который по всей его площади воздействует давление жидкости.
Помимо вышесказанного необходимо упомянуть, что некоторые типы материалов имеют различные механические свойства в зависимости от направления нагрузки. Такие материалы характеризуются как анизотропные. Яркими примерами служит древесина, слоистые пластмассы, некоторые виды камня, ткани и прочее.
У изотропных материалов механические свойства и упругая деформация одинаковы в любом направлении. К ним относят металлы (сталь, чугун, медь, алюминий и прочее), неслоистые пластмассы, естественные камни, бетон, каучук.
Модуль Юнга (упругости)
Все твердые тела, как кристаллические, так и аморфные, имеют свойство изменять свою форму под воздействие приложенной к ним силы. Другими словами, они подвергаются деформации. Если тело возвращается к исходным размерам и форме после того, как внешнее усилие прекращает свое воздействие, то его называют упругим, а его деформацию считают упругой. Для любого тела существует предел приложенного усилия, после которого деформация перестает быть упругой, тело не возвращается в исходную форму и к исходным размерам, а остается в деформированном состоянии или разрушается. Теория упругих деформаций тел была создана в конце 17 века британским ученым Р. Гуком и развита в трудах его соотечественника Томаса Юнга. В их честь Гука и Юнга были названы соответственно закон и коэффициент, определяющий степень упругости тел. Он активно применяется в инженерном деле в ходе расчетов прочности конструкций и изделий.

Общее понятие
При любом внешнем воздействии на предмет, внутри его возникают встречные силы, компенсирующие внешние. Для идеальных систем, находящихся в равновесии, силы равномерно распределены и равны, что позволяет сохранить форму предмета. Реальные системы не подчиняются таким правилам, что может привести к их деформации. Оценивая прочность материалов, говорят об их упругости.
Определение модуля Юнга твердых тел
Упругие материалы – это те, которые после прекращения внешнего воздействия, восстанавливают свою первоначальную форму.
Внутренние силы распределены равномерно по всей площади поперечного сечения предмета, имеют свою интенсивность, которая выражается количественно, называется напряжением (р) и измеряется в Н/м 2 или по международной системе Па.
Напряжение имеет свою пространственную направленность: перпендикулярно площади сечения предмета – нормальное напряжение (σz) и лежащая в плоскости сечения – касательное напряжение (τz).
Опыт с пружинными весами
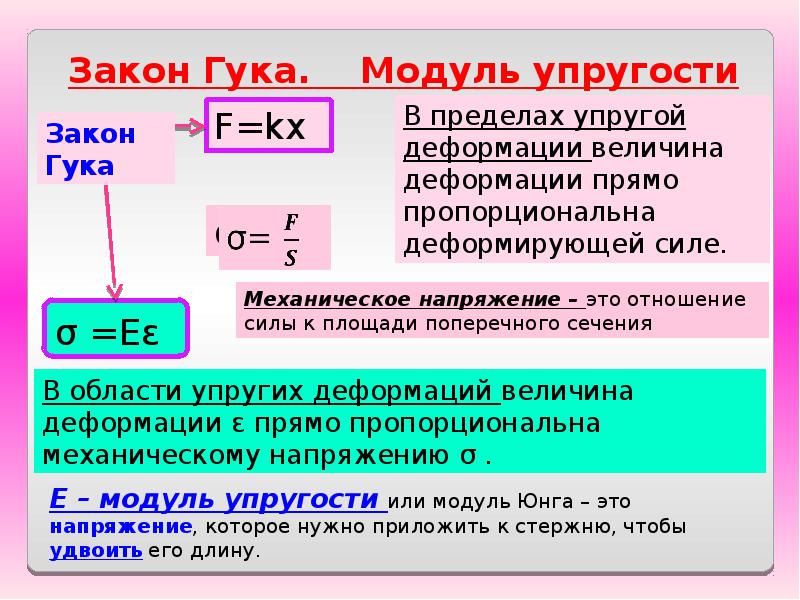
Модуль упругости (Е) как единицу измерения отношения материала к линейной деформации, и нормальное напряжение связывает формула закона Гука:
где ε – относительное удлинение или деформация.
Преобразовав формулу (1) для выражения из нее нормального напряжения, можно увидеть, что Е является постоянной при относительном удлинении, и называется коэффициентом жесткости, а его единицы измерения Па, кгс/мм 2 или Н/м 2 :
Модуль упругости – это единица измерения отношения напряжения, создаваемого в материале, к линейной деформации, такой как, растяжение и сжатие.
В справочных материалах размерность модуля упругости выражается в МПа, так как деформация имеет довольно малое значение. А зависимость между этими величинами обратно пропорциональная. Таким образом, Е имеет высокое значение, определяемое 107-109.
Как определить модуль упругости стали
Выяснить модули упругости для различных марок стали можно несколькими путями:
- по справочным данным из таблиц;
- экспериментальными методами для небольшого образца;
- расчетными методами, зная необходимые данные.
Жесткость стали зависит от ее химического состава и вида кристаллической решетки, от плотности, достигнутой в результате обработки. Прочность же ее конструкций определяется такими важными факторами, как параметры изделия, в том числе габариты, эксплуатационные нагрузки, и их длительность. При расчетах, выполняемых по нормированным методикам, результат осознанно завышают, чтобы предупредить возможные аварии и поломки.
Тем не менее, устойчивость стали к деформации определяется изначально ее маркой, то есть наличием примесей в сплаве.
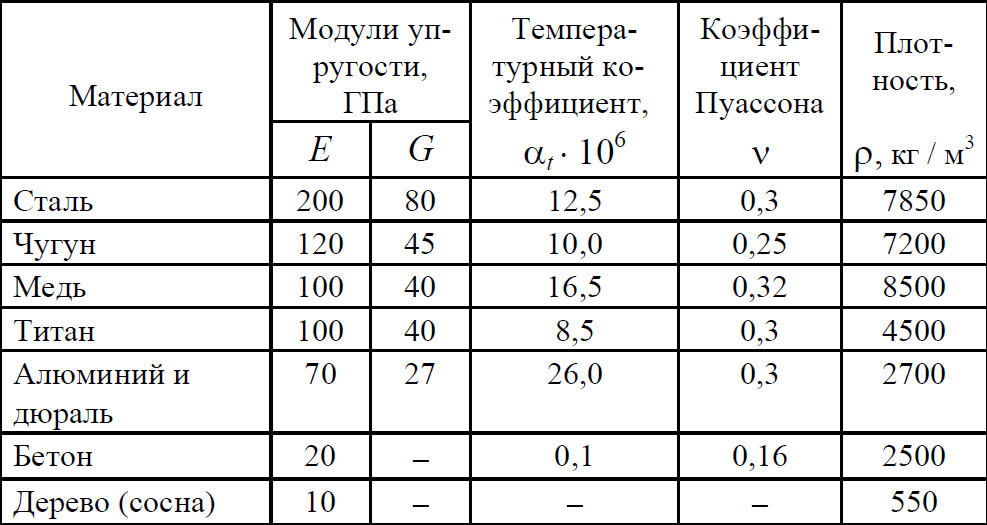
В таблице приведены модули упругости стали наиболее популярных марок, а модуль сдвига ее составляет – 80-81 ГПа.
При расчете строительных конструкций нужно знать расчетное сопротивление и модуль упругости для того или иного материала. Здесь представлены данные по основным строительным материалам.
Таблица 1. Модули упругости для основных строительных материалов
Нормативные данные для рассчетов железобетонных конструкций
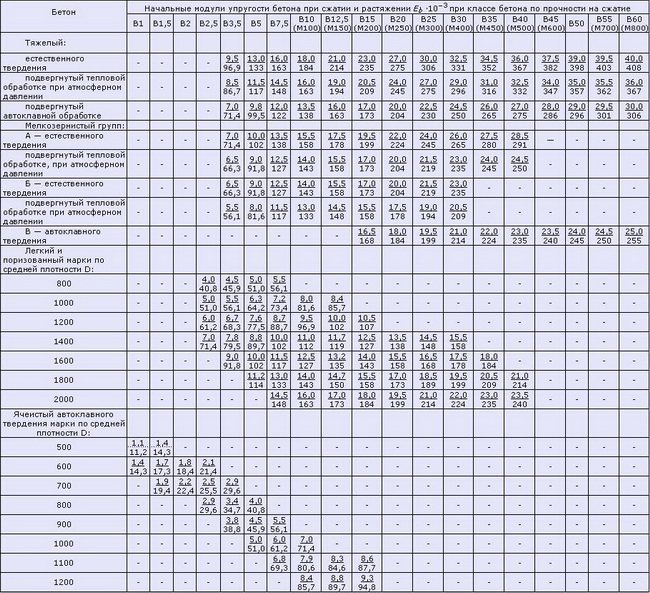
Таблица 2. Модули упругости бетона (согласно СП 52-101-2003)
Таблица 2.1 Модули упругости бетона согласно СНиП 2.03.01-84*(1996)
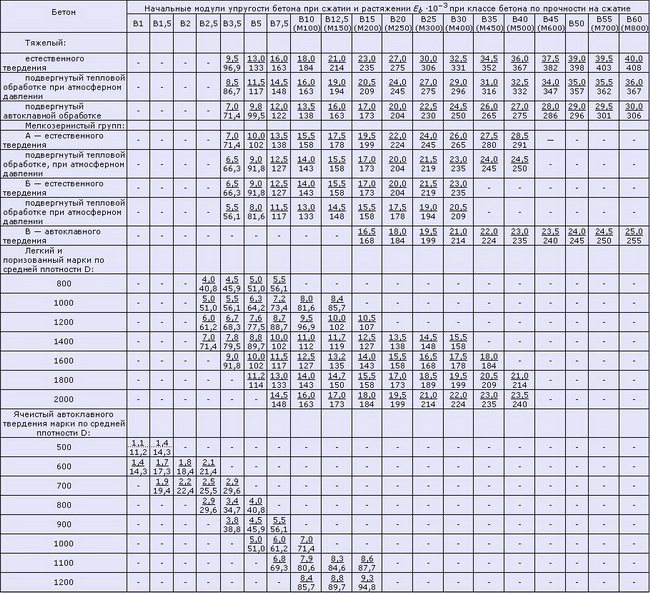
Примечания: 1. Над чертой указаны значения в МПа, под чертой — в кгс/см². 2. Для легкого, ячеистого и поризованного бетонов при промежуточных значениях плотности бетона начальные модули упругости принимают по линейной интерполяции. 3. Для ячеистого бетона неавтоклавного твердения значения Еb принимают как для бетона автоклавного твердения с умножением на коэффициент 0,8. 4. Для напрягающего бетона значения Еb принимают как для тяжелого бетона с умножением на коэффициент a
= 0,56 + 0,006В.
Таблица 3. Нормативные значения сопротивления бетона (согласно СП 52-101-2003)
Таблица 4. Расчетные значения сопротивления бетона сжатию (согласно СП 52-101-2003)
Таблица 4.1 Расчетные значения сопротивления бетона сжатию согласно СНиП 2.03.01-84*(1996)
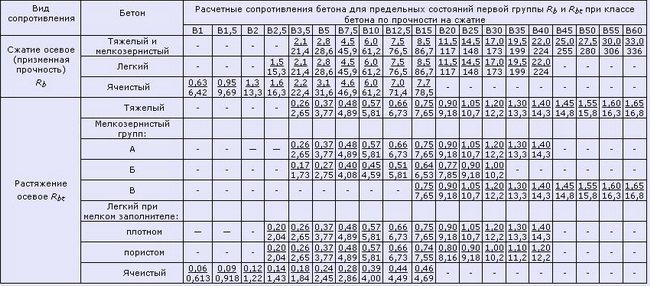
Таблица 5. Расчетные значения сопротивления бетона растяжению (согласно СП 52-101-2003)
Таблица 6. Нормативные сопротивления для арматуры (согласно СП 52-101-2003)
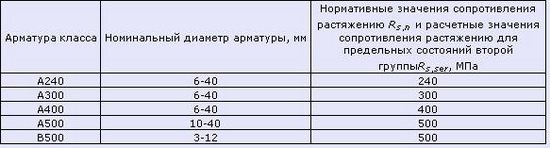
Таблица 6.1 Нормативные сопротивления для арматуры класса А согласно СНиП 2.03.01-84* (1996)

Таблица 6.2 Нормативные сопротивления для арматуры классов В и К согласно СНиП 2.03.01-84* (1996)
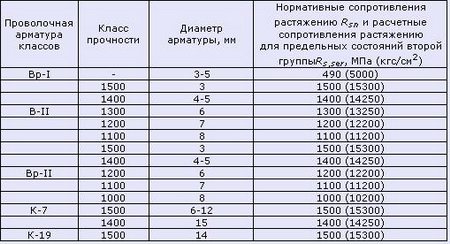
Таблица 7. Расчетные сопротивления для арматуры (согласно СП 52-101-2003)

Таблица 7.1 Расчетные сопротивления для арматуры класса А согласно СНиП 2.03.01-84* (1996)
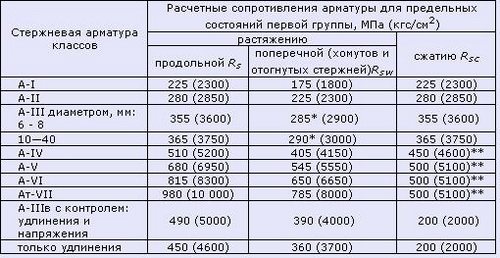
Таблица 7.2 Расчетные сопротивления для арматуры классов В и К согласно СНиП 2.03.01-84* (1996)

Нормативные данные для расчетов металлических контрукций
Таблица 8. Нормативные и расчетные сопротивления при растяжении, сжатии и изгибе (согласно СНиП II-23-81 (1990)) листового, широкополосного универсального и фасонного проката по ГОСТ 27772-88 для стальных конструкций зданий и сооружений
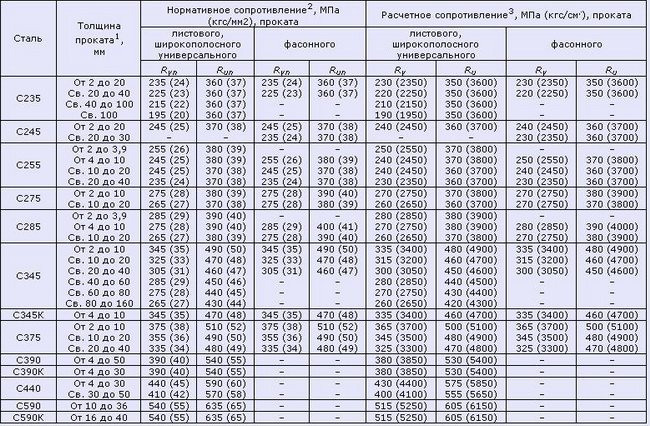
Примечания: 1. За толщину фасонного проката следует принимать толщину полки (минимальная его толщина 4 мм). 2. За нормативное сопротивление приняты нормативные значения предела текучести и временного сопротивления по ГОСТ 27772-88. 3. Значения расчетных сопротивлений получены делением нормативных сопротивлений на коэффициенты надежности по материалу, с округлением до 5 МПа (50 кгс/см²).
Таблица 9. Марки стали, заменяемые сталями по ГОСТ 27772-88 (согласно СНиП II-23-81 (1990))
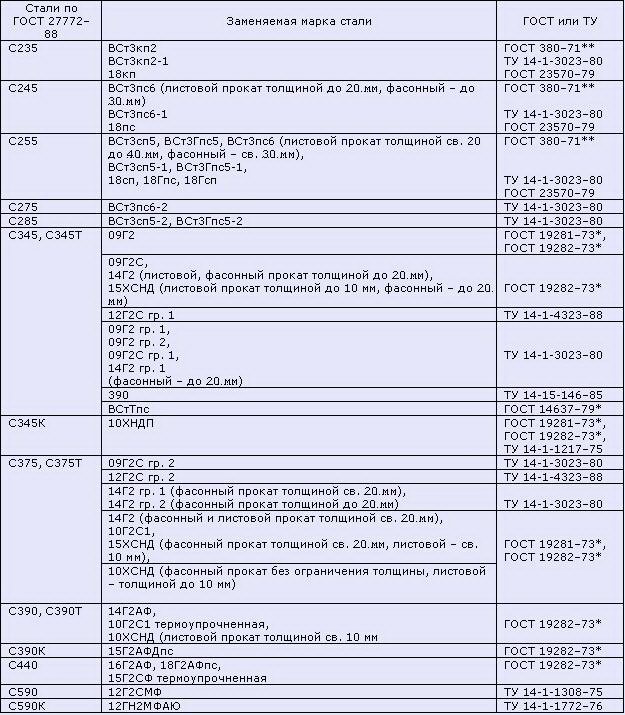
Примечания: 1. Стали С345 и С375 категорий 1, 2, 3, 4 по ГОСТ 27772-88 заменяют стали категорий соответственно 6, 7 и 9, 12, 13 и 15 по ГОСТ 19281-73* и ГОСТ 19282-73*. 2. Стали С345К, С390, С390К, С440, С590, С590К по ГОСТ 27772-88 заменяют соответствующие марки стали категорий 1-15 по ГОСТ 19281-73* и ГОСТ 19282-73*, указанные в настоящей таблице. 3. Замена сталей по ГОСТ 27772-88 сталями, поставляемыми по другим государственным общесоюзным стандартам и техническим условиям, не предусмотрена.
Расчетные сопротивления для стали, используемой для производства профилированных листов здесь не показаны.